0. 2.7.3.Алгоритм модифицированного симплекс-метода.

Шаг 1. Определение включаемого вектора .Вычислить. Для каждого небазисного векторанайти

(2.26)

В задаче максимизации (минимизации) в качестве включаемого в базис вектора выбирается тот, которому соответствует наибольшая по абсолютной величине отрицательная (положительная) величина(при наличии альтернатив выбор делается произвольно). Еслидля всехj, то полученное решение

(2.27)

является оптимальным. В противном случае осуществляется переход к Шагу 2.

Шаг 2. Определение исключаемого вектора .При известном исключаемом векторевычислить:

1. значения текущих базисных переменных, то есть ;

2. коэффициенты ограничений при включаемой в базис переменной, то есть . В качестве исключаемого вектора (как в задаче максимизации, так и в задаче минимизации) должен выбираться такой вектор , которому соответствует

(2.28)

где и-k-е элементыи. Случай , когда все, свидетельствует о неограниченности решения.

Шаг 3. Определение нового базиса. По известной обратной матрицетекущего базиса найти обратную матрицу для нового базиса, используя формулу. Затем положитьи перейти к Шагу 1.

Таблица 2.43

Базисные переменные							Решение
z

На шаге 1 вычисляются коэффициенты z-строки и определяется включаемая в базис переменная. Затем на Шаге 2 путём вычисления элементов правой части таблицы (=) и коэффициентов ограничений при вводимой в базис переменной () определяется исключаемая переменная.

Замечание. Проводя вычисления по схеме модифицированного симплекс-метода, сначала целесообразно записывать получаемые результаты на шагах 1 и 2 в таблице, аналогично приведённой выше.

Пример 2.15:

Максимизировать при ограничениях

Начальное решение

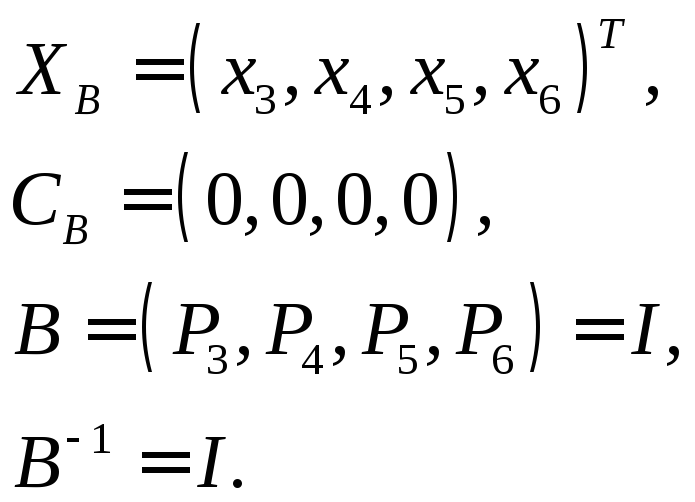
Первая итерация

Шаг 1. Вычисление для небазисных векторов и .

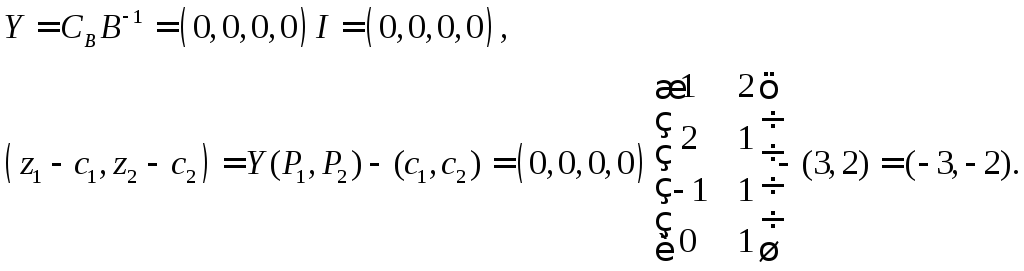
В соответствии с правилами составления симплекс-таблиц результаты, выполненные на данной стадии вычислений, представляются в следующем виде:

Таблица 2.44

Базисные переменные							Решение
z	-3	-2	0	0	0	0

(Заметим, что автоматически обращаются в нуль для всех базисных переменных.) В соответствии с полученными результатами в качестве включаемого в базис вектора выбирается.

Шаг 2. Определение исключаемого вектора при условии введения в базис вектора .

Результаты вычислений на шагах 1 и 2 можно представить в виде следующей таблицы:

Таблица 2.45

Базисные переменные							Решение
z	-3	-2	0	0	0	0	0
	1						6
	2						8
	-1						1
	0						2

Отсюда следует, что

Соответствует переменной . Таким образом, исключению из базиса подлежит вектор.

Шаг 3. Определение обратной матрицы, соответствующей новому базису.

Так как вместо вектора в базис вводится вектори, то

Новому базису соответствуют векторы

Вторая итерация

Шаг 1. Вычисление для небазисных векторов и .

Следовательно, включению в базис подлежит вектор .

Шаг 2. Определение исключаемого вектора при условии ввода в базис вектора .

Результаты вычислений на шагах 1 и 2 алгоритма можно представить в виде следующей таблицы:

Таблица 2.46

Базисные переменные							Решение
z	0	-1/2	0	3/2	0	0
		3/2					2
		1/2					4
		3/2					5
		1					2

Отсюда следует, что

Соответствует переменной . Таким образом, исключению из базиса подлежит вектор.

Шаг 3. Определение новой обратной матрицы.

Так как в базис вместо вектора вводится вектори, то

Новому базису соответствуют векторы

Третья итерация

Шаг 1. Вычисление для векторов и .

Так как для всехj, полученный базис соответствует оптимальному решению.

Оптимальное решение