4. Многопродуктовая задача управления запасами с фиксированным размером заказа

В реальных условиях приходится решать многопродуктовую задачу управления запасами сырья и материалов, вследствие чего возникают вопросы, связанные с ограничениями по транспорту, пропускной способности путей доставки и отпуска продуктов со склада, объемам хранения, размерам денежных сумм, подлежащих одновременной оплате и т.д. В частности, возникает задача равномерного распределения заказов разных ресурсов во времени с сохранением средней суммы оборотных средств, вкладываемых в запасы.

Вначале рассмотрим случай, когда ограничена общая стоимость запаса. Пусть в обращении находится несколько продуктов . При решении допустим те же упрощения, что и в модели Уилсона.

При условии независимости продуктов и их заказов для каждого i-го продукта размеры оптимальных партий будут по формуле Уилсона следующими:

Общая стоимость запасов продуктов в этом случае:

, (2.69)

где С_i – закупочная стоимость единицы i-го продукта,  - нормировочный множитель, учитывающий, что заказы отдельных товаров могут поступать независимо друг от друга (=1\2), или одновременно (=1).

Внесем ограничения на общую стоимость запасов C так, что

(2.70)

Если C_, рассчитанное по формуле (2.69), меньше или равно С, то данное ограничение оказывается избыточным и им можно пренебречь, а искомые размеры заказов Q_i = Q_i^опт рассчитать по формуле Уилсона.

Если же C_, рассчитанное по формуле (2.69), больше C, то наиболее рациональными будут значения размеров заказов при превращении ограничения (2.70) в равенство:

(2.71)

Таким образом, задача сводится к нахождению Q_i, минимизирующих, как и в случае однопродуктовой модели Уилсона, суммарные издержки МТС:

при ограничении .

Эта задача может быть решена методом множителей Лагранжа. Обозначим  стоимость хранения единицы продукции i за период Т как С_i, где С_i – закупочная стоимость i – ой продукции, а  - издержки хранения единицы i – ой продукции за время Т (например, год), выраженные как доля закупочной цены С_i, или процентная ставка (например, годовая).

Строим функцию Лагранжа:

,

где  < 0 – множитель Лагранжа.

Оптимальные значения Q_i и  находим, приравняв к нулю соответствующие производные:

Отсюда (2.72)

Так как ' < 0, то Q_i^опт < Q_i^опт, т.е. размеры партий в случае ограничения на общую стоимость заказа уменьшаются.

Издержки

(2.73)

при этом растут по сравнению со случаем, не учитывающим данное ограничение.

Значения ' в (2.72) можно найти методом последовательных приближений, начиная с ', близких к 0, и постепенно увеличивая его по модулю (знаменатель будет расти, Q_i падать и, следовательно, будет уменьшаться общая стоимость запасов), пока не станет выполняться ограничение.

Аналогично решается задача с ограничением на объем склада. При этом вводится V_i – объем, занимаемый единицей i – ой продукции, V – общий объем склада. В зависимости от характера задачи вводятся ограничения либо по среднему , либо по максимальномууровню запаса. Можнорешить задачу с одновременным учетом этих двух ограничений, либо каких-либо еще.

Усложним теперь задачу, учтя убытки, которые будет нести предприятие, если спрос не удовлетворён. Пусть на предприятии вследствие неудовлетворённого спроса (дефицита) возникают убытки, характеризующиеся величиной С_У на единицу ресурса в единицу времени. Неудовлетворённый спрос покрывается из следующей партии с момента поступления её на склад (рис.2.25). Необходимо определить, какими должны быть максимальные запасы на складе M_i и поставляемая партия Q_i каждого i-того вида материала, чтобы затраты на доставку и хранение с учётом неудовлетворенного спроса были минимальными при ограничении на общую стоимость запасов C (2.71).

В этом случае задача сводится к нахождению M_i и Q_i, минимизирующих суммарные издержки МТС (см. формулу (2.19)):

(2.74)

при ограничении

Выполнив те же обозначения, построим функцию Лагранжа:

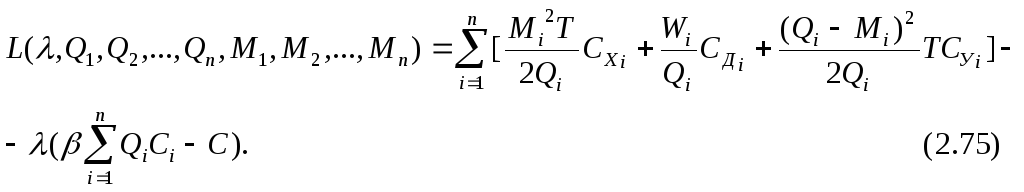Оптимальные значения Q_i, M_i и  находим, приравняв к нулю соответствующие производные:

или после несложных преобразований

Отсюда

или, используя понятие плотности убытков _i,

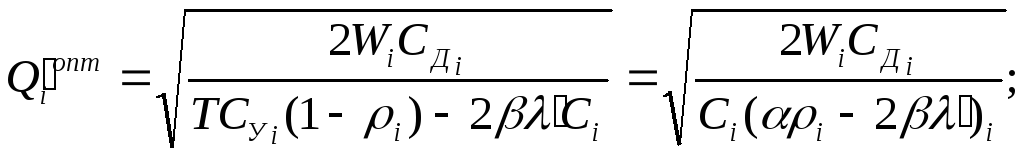(2.76)

(2.77)

Значение ' в (2.76) также находится методом последовательных приближений, начиная с ', близких к 0, и постепенно увеличивая его по модулю, пока не станет выполняться ограничение.

Задача с ограничением на объем склада решается подобным образом, однако в ограничении используется не размер заказа Q_i, а максимальный размер запаса M_i. При этом левая часть ограничения будет иметь вид . При таком ограничении функция Лагранжа примет вид

а производные запишутся следующим образом:

или после несложных преобразований

Отсюда

(2.79)

(2.80)

Значение ' в (6.79) находится методом последовательных приближений, начиная с ', близких к 0, и постепенно увеличивая его по модулю (знаменатель будет расти, M_i падать и соответственно будет уменьшаться общая площадь запасов), пока не станет выполняться ограничение.