Завадостійке кодування

Завадостійкими є такі коди, які дозволяють виявляти або виявляти та виправляти помилки, що виникають у процесі передачі внаслідок дії завад. Як зазначалося вище, при завадостійкому кодуванні з усіх N₀ можливих кодових комбінацій довжиною n символів використовують лише N_д дозволених (тобто частину із N₀).

Усі заборонені комбінації, кількісит яких становить Nз = N₀ – N_д, розбиваються на N_д підмножин М_і, і=1...N_д, і кожній підмножині ставиться у відповідність дозволена комбінація В_і. Правило прийому встановлюють таке: коли прийнята комбінація попала у підмножину М_і, то приймають рішення на користь комбінації В_і. У такому випадку фактично виправляються всі ті помилки, які не виводять передану кодову комбінацію за межі віднесеної до неї підмножини заборонених.

У підмножину М_і повинні бути включені комбінації , при прийомі яких найбільш імовірною переданою комбінацією є В_і. Доцільно, щоб декодер приймав рішення на користь комбінації В_і тоді, коли прийнята комбінація відрізняється від В_і на меншу кількість символів ніж від інших дозволених комбінацій. Таке правило прийняття рішення є оптимальним за критерієм максимуму правдоподібності. У такому випадку рішення приймається на користь В_і, коли умовна ймовірність Р прийняття кодової комбінації при передачі комбінації В_і є максимальною.

Для двійкового симетричного каналу без пам’яті.

Р , (28)

де Р_пом – імовірність спотворення символу,

d - відстань Хемінга між (число розрядів, в яких комбінації відрізняються одна від одної).

Існує два великих класи завадостійких кодів:

блочні (блокові);

безперервні.

(Детальнішу класифікацію див. [1,3,4,6])

При блочному кодуванні послідовність елементарних повідомлень (у вигляді, наприклад, двійкових символів) розбивається на відрізки, кожному з яких ставиться у відповідність певна послідовність (блок) кодових символів, яку звуть кодовою комбінацією. Множина всіх можливих при цьому кодових комбінацій зветься блочним кодом. Коли довжина блоку (кількість символів кодової комбінації) n є постійна величина, – код зветься рівномірним. Коли n = var, - нерівномірним. Як правило використовують рівномірні завадостійкі коди.

Здатність коду виявляти (виправляти) помилки оцінюється кратністю помилок, які він дозволяє виявити (виправити) t_в (t_вип). Кратність помилки це кількість символів кодової комбінації, які спотворені.

Ці величини у свою чергу обумовлені кодовою відстанню d. Для виявлення помилок необхідно, щоб кодова відстань відповідала співвідношенню

d_в 1+t_в; . (29)

для виправлення помилок –

d_вип 1+2t_вип, (30)

де t_в - кратність помилок, що виявляються,

t_вип - кратність помилок, що виправляються.

При цьому деякі помилки більшої кратності можуть також виявлятися (виправлятися).

Необхідна кодова відстань забезпечується шляхом введення надлишковості. Кодова відстань обумовлює потрібну кількість перевірочних (надлишкових) розрядів r у кодовому слові блокового коду. В результаті n-розрядне кодове слово складається із k інформаційних розрядів та r перевірочних розрядів. Їх розташування в межах кодового слова блокового роздільного коду може бути довільним, але відомим приймальній та передавальній стороні.

Надлишковість є одною з характеристик завадостійких кодів, під якою розуміють (для блокових кодів) величину

R= . (31)

Величина зветься відносною швидкістю коду.

Величина r визначається через верхню межу Хемінга

r . (32)

для парного значення t_в.

Або

r (33)

для непарного t_в.

Це співвідношення справедливе для „швидких” кодів, тобто коли .

Для „повільних” кодів, коли , треба використовувати верхню межу Плоткіна

r . (34)

Щоб не перевищити доцільний рівень r користуються нижнею межею Варшамова-Гільберта

r . (35)

Найбільш поширеними способами опису блокових кодів є матричний та поліноміальний.

Матричний опис блокових лінійних кодів.

Матричне представлення кодів є досить зручним. В першу чергу це стосується систематичних ( ) кодів.

Усі їх дозволені комбінації можна отримати маючи вихідних (базисних) лінійно незалежних дозволених комбінацій. Ці комбінації повинні задовольняти таким умовам[3]:

1. до числа базисних комбінацій не може входити нульова комбінація;

2. кодова відстань між будь – якими парами базисних комбінацій не може бути меншою ;

3. кожна базисна комбінація повинна мати кількість одиниць не менше (це стосується будь–якої дозволеної)

4. всі базисні комбінації повинні бути лінійно незалежними.

Базисні комбінації представляють у вигляді матриці розмірності кxп

G= . (36)

Цю матрицю називають породжуючою. Процес кодування полягає у виконанні операції

В=А×G, (37)

де: А – вектор розмірності 1×k, який відповідає повідомленню, що підлягає кодуванню,

В – вектор розмірності 1×n, який відповідає дозволеній кодовій комбінації даного коду.

Матрицю G можна представити у вигляді двох підматриць: інформаційнoї матриці І розмірності k×k, яку зручно обирати одиничною, та матриці перевірочних символів Р розмірності k×r (де r=n-k)

G = . (38).

Лінійний (n,k) код може бути заданий перевірочною матрицею Н розмірності r×n. Тоді для кодової комбінації, яка належить даному коду, виконується

ВН^Т =0 , (39)

де символ ^Т означає транспонування матриці.

Канонічна форма матриці Н має вигляд

Н=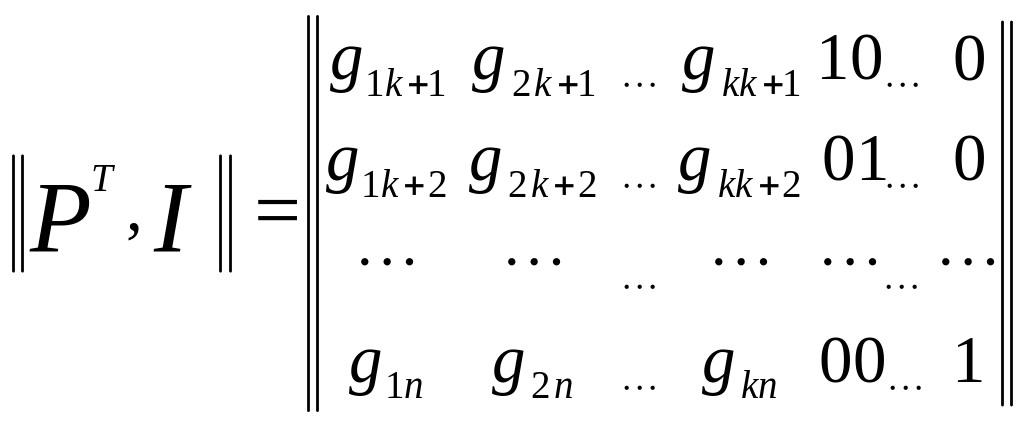 . (40)

Кодуючий пристрій лінійного ( ) коду[1] складається із k розрядного регістру зсуву та r блоків суматорів за модулем 2. Інформаційні символи подають на вхід регістру і на вихід кодуючого пристрою через ключ, який після приходу k-го інформаційного символу починає покроково підключатися до виходів суматорів починаючи з першого і до r-го (для видачі на вихід кодера перевірочних символів від в_k+1 до в_п).

Процес декодування полягає у виконанні операції

S=BH^T, (41)

де S – вектор синдрому розмірності 1×r,

B- вектор прийнятої комбінації.

У випадку, коли прийнята кодова комбінація співпадає з одною із дозволених, вектор S=0.

Вектор S≠0 у випадку, коли мало місце спотворення кодової комбінації, яке можна представити дією вектора помилок Е (таких, що даний код виявити може; при наявності помилок,які не виявляються, S=0).

А саме

S= B H^T=(B E)H^T=EH^T, (42)

де B - вектор спотвореної прийнятої комбінації,

символ - складання за модулем 2.

Декодер лінійного коду складається [1] з k-розрядного регістру із зсувом, r блоків суматорів за модулем 2, r схем порівняння прийнятих перевірочних розрядів з отриманими у ході декодування і аналізатора помилок. Іншими словами, декодер таким же чином, як і кодер, отримує перевірочні розряди на основі інформаційних розрядів, що містяться у інформаційній частині прийнятої кодової послідовності, і порівнює їх з прийнятими перевірочними розрядами. На основі порозрядного порівняння робиться висновок про наявність помилки, а при можливості і про той (ті) розряд(и), де вона має місце. У останньому випадку її можна виправити.

Поліноми (багаточлени) зручно застосувати для опису циклічних кодів. При такому представленні значення двійкових розрядів кодового слова відіграють роль коефіцієнтів при ступенях х . Наприклад, двійкове повідомлення 10011 можна представити у вигляді багаточлена

.

Усі операції з багаточленами здійснюються за законами алгебри, за винятком того, що складання здійснюється за модулем 2: x^a x^a=0; x^a 0=x^a; 0 0=0.

Циклічні коди відрізняються високою ефективністю виявлення помилок і порівняно простою реалізацією кодуючих і декодуючих пристроїв у вигляді регістрів з зсувом і зворотними зв’язками.

Циклічний код це код, у якого з приналежної йому комбінації

а₀, а₁ , а₂ ... а_n-1,.. a_n

шляхом циклічної перестановки отримують також дозволену комбінацію

a_n, a_0, a₁...a_n-2, a_n-1.

Дозволеними комбінаціями циклічного коду є такі комбінації, які діляться на деякий вихідний (утворюючий) багаточлен Р(х), який має ступінь r. Комбінація з помилкою (з діапазону тих помилок, що може виявити даний код) після ділення на Р(х) дасть залишок відмінний від нуля, що свідчить про наявність спотворення у прийнятій комбінації.

Один із можливих варіантів кодування при застосуванні циклічних кодів передбачає, що багаточлен G(x), який відображає двійковий код призначеного для передачі повідомлення, помножують на х^r, де r – ступінь поліному Р(х). Це збільшує довжину кодової комбінації на r розрядів, які потрібні для запису у них перевірочних розрядів.

Добуток G(x) x^r ділять на утворюючий поліном Р(х), а залишок R(x) від цього ділення дописують до G(x) x^r, тобто записують залишок у r молодших розрядів(де після зсуву – перемноження на х^r записані нулі). Отриманий поліном F(x)= G(x) x^r R(x) є комбінацією, що ділиться без залишку на Р(х), тобто він є дозволеною комбінацією даного циклічного коду.

Дійсно, якщо f(x) є частка від ділення G(x) x^r на Р(х), то

G(x) x^r = f(x) P(x) R(x). (43)

Додавши за модулем 2 до правої та лівої частини R(x) отримуємо

G(x) x^r R(x)= f(x) P(x), (44)

Тобто, комбінація F(x) =G(x) x^r R(x) дійсно ділиться на Р(х) без залишку.

До циклічних кодів відносяться коди Боуза-Чоудхурі-Хоквінгема (БЧХ).

Кодуючі та декодуючі пристрої циклічних кодів будують на основі регістрів зсуву з зворотними зв’язками.

Такі регістри здійснюють операцію ділення, яка полягає у послідовному складанні за модулем 2 дільника із старшими розрядами діленого або отриманого на черговому кроці ділення залишку. Регістри складаються з тригерів.

Регістр зсуву з зворотними зв’язками будується у відповідності до обраного утворюючого багаточлена за такими формальними правилами (теоретичною базою побудови таких пристроїв є теорія кінцевих автоматів з пам’яттю):

1. Число каскадів (тригерів) регістра обирають рівним степені ( ) утворюючого багаточлена.

2. Кількість суматорів за модулем 2 береться на одиницю менше числа ненульових членів утворюючого багаточлена.

3. Входи всіх тригерів регістра позначають х^і (і=0, 1, 2). Вихід останнього тригера позначається , а вхід першого – х⁰.

4. Суматори за модулем 2 встановлюються на вході тих тригерів, для яких у формулі утворюючого багаточлена коефіціент при відповідній степені х^і має ненульове значення. Наприклад, для Р(х) =х³+х+1 (див. рис. 3) суматори встановлюються на входах першого та другого тригерів (тригерів, що відповідають х⁰ та х).

5. Вихід останнього тригера з’єднується з одним із входів суматорів.

6. Виходи попередніх тригерів з’єднуються з входами наступних через суматори (в залежності від того, встановлені вони між тригерами чи ні) або безпосередньо.

Кл1

Кл2; Вих

Х⁰ Х¹ Х²

Рис. 3

Робота пристрою відбувається наступним чином.

Нехай, наприклад, при кодуванні діленню на зазначений поліном підлягає комбінація 01010. У вигляді поліному це G(x) = x³ + x. Після множення на x³ отримуємо G(x)∙x³ = x⁶ + x⁴. Відповідна двійкова комбінація 01010000 покроково подається на вхід регістру (див. рис. 3) починаючи із старшого розряду (див. Таблицю 1).

Таблиця 1

№кроку	Вхідна послідовність	Стан тригерів
		X0	X1	X2
1	0000101	0
2	000010	1	0
3	00001	0	1	0
4	0000	1	0	1
5	000	1	0	0
6	00	0	1	0
7	0	0	0	1
8		1	1	0

На першому кроці старший розряд вхідної послідовності (символ 0) через перший суматор за модулем 2 записується у перший тригер (суматори за модулем 2 перший та другий не впливають на стан тригерів бо перший ключ (Кл1) розімкнений).

На другому кроці цей символ зсувається у другий тригер, а другий символ вхідної послідовності (1) записується у перший тригер.

На третьому кроці символ 0 із другого тригера переноситься у третій тригер, символ 1 із першого тригера у другий, а третій символ вхідної послідовності (0) записується у перший тригер. Після r-того кроку (у прикладі, що розглядається, - після третього) замикається Кл1 і розмикається другий ключ (Кл2). Тому на наступних кроках зворотній зв’язок починає впливати на стан тих тригерів (розрядів), перед якими встановлені суматори за модулем 2.

На четвертому кроці одиниця четвертого розряду вхідної послідовності поступає на перший вхід першого суматора за модулем 2, на другий вхід якого із третього тригера через ключ 1 поступає 0. За результатом додавання цих чисел за модулем 2 на виході суматора формується одиниця, яка записується у перший тригер. Нуль, який знаходився до цього у першому тригері, подається на перший вхід другого суматора за модулем 2, де до нього додається нуль, що прийшов на другий вхід цього суматора через ключ 1. За результатом додавання цих чисел за модулем 2 на виході другого суматора формується нуль, який записується у другий тригер, а одиниця із другого тригера безпосередньо переписується у третій тригер.

На п’ятому кроці нуль п’ятого розряду вхідної послідовності поступає на перший вхід першого суматора за модулем 2, на другий вхід якого із третього тригера через ключ 1 поступає одиниця. За результатом додавання цих чисел за модулем 2 на виході суматора формується одиниця, яка записується у перший тригер. Одиниця, яка знаходилась до цього у першому тригері, подається на перший вхід другого суматора за модулем 2, де до неї додається одиниця, що прийшла на другий вхід цього суматора через ключ 1. За результатом додавання цих чисел за модулем 2 на виході другого суматора формується нуль, який записується у другий тригер, а нуль із другого тригера безпосередньо переписується у третій тригер.

На подальших кроках подібні процедури продовжуються і на n-ному (у даному прикладі на восьмому) кроці отримано залишок, який дорівнює (записуємо починаючи із старшого розряду) 011, що відповідає поліному R_I(x)= x+1 і дозволяє сформувати кодове слово завадостійкого коду, заданого поліномом Р(х) =х³+х+1. Для розглянутого прикладу це кодове слово у двійковому вигляді буде мати вигляд 01010011, а у поліноміальному F(x) = x⁶ + x⁴ + x + 1.

Для повторення і закріплення матеріалу з теми 3 доцільно самостійно відповісти на такі контрольні питання.

1. Коди, способи представлення кодів, поняття про кодування.

2. Що розуміють під кодуванням у широкому та у вузькому смислі?

3. Що називають кодом?

4. Основні параметри кодів.

5. Різновиди кодів.

6. Цілі кодування.

7. Кодування для каналу без шумів.

8. Мета і принципи побудови завадостійких (коректувальних) кодів.

9. Класифікація, коректувальні властивості і показники якості завадостійких кодів.

10. Блочні циклічні та каскадні коди.

11. Ланцюгові коди.

12. Алгоритми та пристрої кодування і декодування.

13. Підвищення достовірності передачі інформації на основі коректувального кодування.

14. Відстань Хемінга і як вона розраховується?

15. За якими ознаками класифікують коди?

16. Як класифікуються коди за величиною m?

17. Як класифікуються коди за основою?

18. Як класифікуються коди за величиною n?

19. Як класифікуються коди за значністю?

20. Як класифікуються коди за порядком передачі символів у часі?

21. У чому різниця між паралельним та послідовним кодом?

22. Як класифікуються коди за вагою?

23. Що таке одиничний код?

24. Що таке багатопозиційний код?

25. Що таке код Грея?

26. Що таке код з постійною вагою?

27. Що таке код з перевіркою на парність?

28. У чому суть рівномірного та нерівномірного кодування? Дати порівняльну характеристику.

29. Позиційні коди.

30. Непозиційні коди.

31. Составні коди.

32. Рефлексні коди.

33. Що таке завадостійкий код?

34. Що лежить в основі завадостійкого кодування?

35. Кодова відстань і як вона визначається.

36. Яке максимальне (мінімальне) значення може мати відстань Хемінга?

37. Яке максимальне (мінімальне) значення може мати кодова відстань ?

38. Яке максимальне (мінімальне) значення може мати кратність помилки у блочному (n, k) коді?

39. Що таке блочний код?

40. Що таке безперервний код?

41. Які коди звуть систематичними?

42. Що таке кратність помилки?

43. Що таке вектор помилки?

44. Що таке поліном помилки?

45. Яка різниця між вектором помилки і поліномом помилки?

46. Що загального між вектором помилки і поліномом помилки?

47. Яку максимальну ступінь може мати поліном помилки при відомій значності коду?

48. Яку мінімальну ступінь може мати поліном помилки?

49. На що вказує кількість ненульових членів поліному помилки?

50. На що вказує кількість нульових членів поліному помилки?

51. На що вказують ступені ненульових членів поліному помилки?

52. Вкажіть зв’язок кодової відстані з кратністю помилок, що виявляються.

53. Поясніть зв’язок кодової відстані з кратністю помилок, що виправляються.

54. Довести теоретично, що залишок від ділення A(x)x^r на P(x), доданий за модулем 2 до A(x)x^r, утворює поліном, який ділиться на P(x) без залишку.

55. Яким вимогам повинні задовольняти базові комбінації лінійного коду?

56. Що таке примітивний код?

57. Що таке рівнодоступний код?

58. Яку функцію виконує кодер каналу?

59. Яку функцію виконує кодер джерела?

60. Як представляють числа у системі залишкових класів?

61. Як визначити кількість перевірочних розрядів у кодовій комбінації завадостійкого рівномірного блочного коду?

62. Як визначити ступінь утворюючого поліному циклічного коду?

63. Які поліноми можуть застосовуватись у якості утворюючих?

64. Побудова кодерів (декодерів) циклічних кодів.

65. Структура утворюючої матриці лінійного (n,k) коду при розташуванні інформаційних розрядів на початку ( у кінці) кодового слова.

66. Як пов’язані між собою утворююча та перевірочна матриці лінійного коду?

67. Як можна задати лінійний код?

Здійснити розрахунки при розв’язанні таких задач.

Яку розрядність повинен мати кодер джерела при представленні у двійковому коді алфавіту із 26 (56; 72; ) символів?

Яку мінімальну розрядність повинен мати двійковий код у системі дистанційного управління вибором номеру телевізійного каналу, якщо кабельна мережа телебачення транслює до 150 (120; 60; 30) каналів?

Представити у одиничному коді число 9 (12; 15; 8; 13).

Записати у вигляді поліному за основою 2 (3; 4; 5; 6; 7; 8; 9; 10) число 9 (19; 15; 8; 13; 25; 52; 65; 72; 121; 130).

Представити у двійковому коді числа 9 (19; 15; 8; 13; 25; 52; 65; 72; 121; 130; 250; 312; 500; 502; 510; 1023).

Представити у шістнадцятковому коді числа 9 (19; 15; 8; 13; 25; 52; 65; 72; 121; 130).

Представити у вісімковоиу коді числа 9 (19 15 8 13 25 (52; 65; 72;

Представити у двійково-десятковому коді числа 9 (19 15 8 13 25 (52; 65; 72;

Представити у коді Грея числа від 1 до 8 (16; 32).

Представити у непозиційному коді (у системі залишкових класів) число 9 (19; 15; 81; 103; 240; 325; 415).

Визначити необхідну величину ваги коду з постійною вагою при значності n =7 і необхідності передавати інформацію про 30 (20; 25; 40) подій.

Визначити відстань Хемінга між комбінаціями, якими представляються у двійковому коді за номером літери у алфафіті (у коді МТК №2) послідовності літер АБ і ВД.

Визначити відстані Хемінга між комбінаціями, якими представляються у двійковому коді за номером літери у алфафіті (у коді МТК №2; у коді ASCII; у коді KOI-7; у коді KOI-8) літери Ваших ініціалів.

Порівняти можливості щодо виявлення та виправлення помилок кодів, що мають кодові відстані 4 та 5 (5 та 6; 6 та 7; 7 та 8; 8та 9; 9 та 10)

Перевірити наявність помилки при прийомі кодової комбінації 1010101. Утворюючий поліном має вигляд P(x) = x³ + x² + 1.

Визначити вигляд інформаційної комбінації, яка повинна видаватися у декодер отримувача інформації (джерела), при прийомі кодової комбінації виду 1011100, що належить завадостійкому циклічному коду, заданому поліномом P(x) = x³ + x² + 1.

Визначити, чи буде виявлена помилка, поліном якої має вигляд E(x) = x² + 1, декодером циклічного коду, заданого поліномом P(x) = x⁴ + x² + x + 1.

Двійкове число має вигляд А = 100110 (011101; 111010; 101101; 111001; 110010; 101011); породжуюча підматриця лінійного коду

Р = .

Визначити вигляд породжуючої матриці, при необхідності розміщення інформаційних розрядів на початку (у кінці) кодової комбініції, вигляд кодової комбініції, що буде сформована кодером, відносну швидкість, надлишковість коду та кратність помилок, які він може виявляти.

Визначити ступінь утворюючого поліному циклічного коду, який повинен забезпечити виявлення помилок кратності 2 (3; 4; 5; 6;7; 8; 9) при довжині інформаційної частини слова 4(5;6;7;8;9;10;11;12).

Визначити ступінь утворюючого поліному циклічного коду, який повинен забезпечити виявлення помилок кратності 2 (3; 4; 5; 6;7; 8; 9) при необхідності передавати двійкові повідомлення із 4(5;6;7;8;9;10;11;12) символів.

Визначити ступінь утворюючого поліному циклічного коду, який повинен забезпечити виправлення помилок кратності 2 (3; 4; 5; 6;7) при довжині інформаційної частини слова 4(5;6;7;8;9;10;11;12).

Визначити ступінь утворюючого поліному циклічного коду, який повинен забезпечити виправлення помилок кратності 2 (3; 4; 5; 6;7) при необхідності передавати двійкові повідомлення із 4(5;6;7;8;9;10;11;12) символів.

Визначити розмірність породжуючої матриці коду, який повинен забезпечити виявлення помилок кратності 2 (3; 4; 5; 6;7; 8; 9) при довжині інформаційної частини слова 4(5;6;7;8;9;10;11;12).

Визначити розмірність породжуючої матриці коду, який повинен забезпечити виявлення помилок кратності 2 (3; 4; 5; 6;7; 8; 9) при довжині кодового слова 4(5;6;7;8;9;10;11;12).

Визначити розмірність породжуючої матриці коду, який повинен забезпечити виправлення помилок кратності 2 (3; 4; 5; 6;7) при довжині інформаційної частини слова 4(5;6;7;8;9;10;11;12).

Визначити розмірність породжуючої матриці коду, який повинен забезпечити виправлення помилок кратності 2 (3; 4; 5; 6;7) при довжині кодового слова 4(5;6;7;8;9;10;11;12).

Визначити ступінь утворюючого поліному циклічного коду та вибрати можливий до застосування утворюючий поліном при умові, що код повинен забезпечувати виявлення помилок кратності 2 (3; 4; 5; 6;7; 8; 9) при довжині інформаційної частини слова 4(5;6;7;8;9;10;11;12).

Визначити ступінь утворюючого поліному циклічного коду та вибрати можливий до застосування утворюючий поліном при умові, що код повинен забезпечувати виправлення помилок кратності 2 (3; 4; 5; 6;7) при довжині інформаційної частини слова 4(5;6;7;8;9;10;11;12).

Відобразити у тримірному просторі розташування кодових комбінацій двійкового тризначного коду; пояснити, які кодові комбінації доцільно використовувати для передачі повідомлень 1 та 0 і які при цьому можливості буде мати код щодо виявлення та виправлення помилок.

Відобразити у тримірному просторі розташування кодових комбінацій двійкового тризначного коду; пояснити, які кодові комбінації доцільно використовувати для передачі повідомлень 1; 2; 3; 4 і які при цьому можливості буде мати код щодо виявлення та виправлення помилок.

Відобразити у двомірному просторі розташування кодових комбінацій двійкового двозначного коду; пояснити, які кодові комбінації доцільно використовувати для передачі повідомлень 1; 2 і які при цьому можливості буде мати код щодо виявлення та виправлення помилок.

Відобразити у лінійному просторі розташування кодових комбінацій двійкових кодів, дозволені кодові комбінації яких мають кодові відстані, відповідно, 2 і 3 ( 2 і 4; 3 і 4; 3 і 5 ); пояснити можливості цих код щодо виявлення та виправлення помилок.