Б. Деление отрезка в данном отношении

Пусть М₁ (х₁, у₁ ) и М₂ (х₂, у₂ ) – различные точки плоскости. Пусть, далее, точка М (х, у ) лежит на отрезке М₁М₂ и делит его в отношении ₁: ₂, т.е. М₁М:ММ₂ = ₁ : ₂. Требуется выразить координаты х и у этой точки через координаты концов отрезка М₁М₂ и числа ₁ и ₂.

Рис.14. Рис.15.

Задача 3. Найти координаты центра тяжести М треугольника с вершинами в точках М₁(х₁, у₁), М₂(х₂, у₂ ), М₃(х₃, у₃ ).

 Известно, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15 ). Тем самым, ее координаты х и у можно найти по формулам

г де х и у– координаты второго конца М  медианы М₃М. Т.к. М - середина отрезка М₁М₂, то

Эти соотношения позволяют выразить координаты х и у центра тяжести М  М₁М₂ М₃ через координаты его вершин

Замечание. Если точка М (х, у, z ) делит отрезок с концами М₁ (х₁, у₁, z₁ ) и М₂ (х₂, у₂, z₂ ) в отношении ₁: ₂, то ее координаты вычисляются по формулам

2. Полярные координаты

Пусть задана т.О, ось , содержащая т.О, и масштабный отрезок (эталон длины)

(рис. 16). Пусть М – произвольная точка плоскости, отличная от т.О (рис. 17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием r между т.т.О и М и отсчитываемым против часовой стрелки углом  между положительным лучом оси и лучом ОМ с началом в т.О. Пару (r,  ) называют полярными координатами точки М; r – полярный радиус точки М;  - полярный угол. Точка О называется полюсом, - полярной осью.

Ясно, что r > 0, 0    2. Если точка М совпадает с полюсом, то считаем r = 0; полярный угол  в этом случае не определен.

Таким образом, на плоскости можно задать еще одну координатную систему - полярную.

Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат О (0, 0) – полюс, ось Ох – полярная ось, а ось Оу составляет с осью Ох прямой угол. Тогда

Пример. Пусть R > 0 – заданное число. Множество точек плоскости, полярные координаты ( r,  ) которых удовлетворяют равенству r = R, является окружностью радиуса R с центром в полюсе ( рис. 19 ).

Рис. 16 Рис. 17 Рис. 18 Рис. 19

2. Определители 2-го и 3-го порядков

Пусть имеем четыре числа а₁₁, а₁₂, а₂₁, а₂₂ ( читается – «а – один – один», «а – один – два», «а – два – один», «а – два– два» ).

Определителем ( детерминантом ) второго порядка называется число а₁₁ а₂₂ – а₁₂ а_21.

Элемент а_ij определителя стоит на пересечении его i-ой строки и j-го столбца.

Числа а₁₁, а₁₂, а₂₁, а₂₂ - элементы определителя; пары элементов а₁₁, а₁₂ и а₂₁, а₂₂ образуют строки определителя, а пары элементов а₁₁, а₂₁ и а₁₂, а₂₂ - его столбцы; пара элементов а₁₁, а₂₂ образует главную диагональ определителя, а пара а₁₂, а₂₁ - побочную диагональ. Т.о.,

для вычисления определителя второго порядка нужно из произведения

а ₁₁ а₂₂ элементов главной диагонали вычесть произведение а₁₂ а₂₁ элементов его побочной диагонали.

Пусть теперь даны девять чисел а_ij ( i = 1, 2, 3; j = 1, 2, 3 ).

Определителем третьего порядка называется число , (2)

вычисляемое по следующему правилу:

а₁₁ а₂₂ а₃₃ + а₁₂ а₂₃ а₃₁ + а₂₁ а₃₂ а₁₃ - а₁₃ а₂₂ а₃₁ – а₂₁ а₁₂ а₃₃ - а₁₁ а₂₃ а_32. (3)

Первый индекс i элемента а_ij указывает номер строки, в которой

о н расположен, а второй индекс j - номер столбца. Элементы а₁₁,

а₂₂ , а₃₃ образует главную диагональ определителя , а элементы

а₁₃, а₂₂ , а₃₁ - побочную диагональ. При вычислении определителей

3-го порядка удобно пользоваться правилом треугольников ( или

Саррюса ), которое символически представлено на рис. 20. Рис. 20

При помощи разложений ( 1 ) и ( 3 ) легко проверяются некоторые свойства определителей 2-го и 3-го порядков ( свойства 4 – 6, кроме того, легко выводятся из свойств 1 – 3 ) :

1. Величина определителя не изменится, если все его строки заменить столбцами с теми же номерами.

2. При перестановке любых двух строк ( или любых двух столбцов ) определителя он изменяет свой знак на противоположный.

3. Общий множитель всех элементов одной строки ( или одного столбца ) можно вынести за знак определителя.

4. Если определитель имеет две равные строки ( или два равных столбца ), то он равен нулю.

5. Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.

6. Если соответствующие элементы двух строк ( или двух столбцов ) пропорциональны, то определитель равен нулю.

Минором M_ij элемента а_ij определителя  (2) называется определитель, получаемый из данного путем вычеркивания элементов i-ой строки и j-го столбца, на пересечении которых находится этот элемент. Например, минором элемента а₂₃ будет определитель

Алгебраическим дополнением А_ij элемента а_ij определителя  (2) называется минор M_ij этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент а_ij, есть число четное, и с противоположным знаком, если это число нечетное:

Аij = (–1) i + jМij

Теорема. Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения:  = аi 1 А i 1 + аi 2 А i 2 + аi 3 А i 3, i = 1, 2, 3; (4)  = а1 j А1 j + а2 j А2 j + а3 j А3 j, j = 1, 2, 3. (5)

 Покажем, например, что  = а₁₁ А ₁₁ + а_{1 2} А _{1 2} + а_{1 3} А _{1 3}. Пользуясь формулой (3), получаем, что

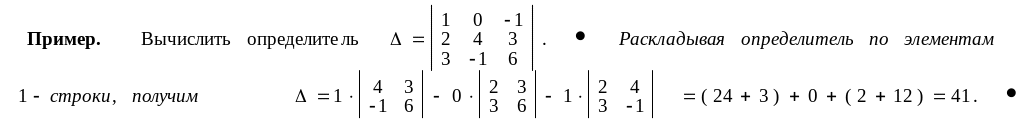 = а₁₁ (а_{2 2} а_{3 3} – а_{3 2} а_{2 3} ) + а_{1 2} (а_{2 3} а_{3 1} – а₂₁ а_{3 3} ) + а_{1 3} (а_{2 1} а_{3 2} – а_{3 1} а_{2 2} ) =

Правило (4 ) называется разложением определителя по элементам i-ой строки, а правило (5 ) - разложением определителя по элементам j-го столбца.