
- •Контрольная работа №12
- •Контрольная работа №2
- •Найти производную функции:
- •Найти значения х, при которых значения производной функции положительны
- •Контрольная работа №3
- •Найти экстремумы функции
- •Построить график функции
- •Контрольная работа №4
- •Контрольная работа №5
- •Контрольная работа №6
- •В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается 1 шар. Какова вероятность того, что это или белый, или красный шар?
- •В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты белый и черный шары?
- •В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трех случайным образом вынутых цветков окажется, по крайней мере, одна гвоздика?
- •Контрольная работа №8
- •Найти множество точек координатной плоскости, удовлетворяющих уравнению:
- •Найти множество точек координатной плоскости, удовлетворяющих неравенству:
- •Контрольная работа № 5.1
- •Вычислите скалярное произведение векторов и , если
- •Дан куб abcda1b1c1d1. Найдите угол между прямыми ad1и вм, где м – середина ребра dd1
- •Контрольная работа № 6.1
- •Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 450 к нему. Найдите длину линии пересечения сферы этой плоскостью.
- •Контрольная работа № 7.1
- •Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60°. Найдите отношение объемов конуса и шара
В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается 1 шар. Какова вероятность того, что это или белый, или красный шар?
Решение
Всего в коробке 3+2+4=9 шаров. Вероятность вытащить белый шар равна р1=2/9 (две ситуации успеха из 9-ти возможных ситуаций). Вероятность вытащить красный шар равна р2=4/9 (четыре ситуации успеха из 9-ти возможных ситуаций). Искомая вероятность равна Р=р1+р2=2/9+4/9=6/9=2/3
Вероятность попадания по мишени стрелком равна 19/20. Какова вероятность: 1) непопадания по мишени при одном выстреле? 2)Попадания по мишени в каждом из двух последовательных выстрелов? 3) Попадания при первом и промахе при втором выстреле?
Решение
Р1=1-19/20=1/20
Р2=19/20=Р3. Поэтому, Р=Р2*Р3=19/20*19/20=361/400=0,9
Вероятность попадания при выстреле равна Р2=19/20. Вероятность промаха при выстреле равна Р1=1/20. Поэтому, Р=Р2*Р1=19/20*1/20=19/400=0,05
В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты белый и черный шары?
Решение
I Рассмотрим ситуацию, когда вначале вынут белый шар, а затем черный
р1 – вероятность вынуть белый шар, р1=4/7, т.к. белых шаров 4 из 7
р2 – вероятность вынуть черный шар, р2=3/6, т.к. один шар мы уже вытащили, а черных шаров 3 из 6.
Поэтому, вероятность данного случая равна
Р3=4/7*3/6=2/7=0,29
II Рассмотрим теперь ситуацию, когда вначале вынут черный шар, а затем белый
р4 – вероятность вынуть черный шар, р4=3/7, т.к. черных шаров 3 из 7
р5 – вероятность вынуть белый шар, р5=4/6, т.к. один шар мы уже вытащили, а белых шаров 4 из 6.
Поэтому, вероятность данного случая равна
Р6=3/7*4/6=2/7=0,29
Искомая вероятность равна Р=Р3+Р6=2/7+2/7=4/7=0,57
В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трех случайным образом вынутых цветков окажется, по крайней мере, одна гвоздика?
Решение
Возможны следующие ситуации:
Среди трех вынутых случайным образом цветков, окажется ровно 1 гвоздика. Обозначим вероятность данного события через Р(1)
Среди трех вынутых случайным образом цветков, окажутся 2 гвоздики. Обозначим вероятность данного события через Р(2)
Среди трех вынутых случайным образом цветков, окажутся 3 гвоздики. Обозначим вероятность данного события через Р(3)
Р(1)=
Р(2)=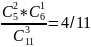
Р(3)=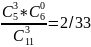
Искомая вероятность равна Р=Р(1)+ Р(2)+ Р(3)=5/11+4/11+2/33=29/33
Контрольная работа №8
Базовый уровень
Найти множество точек координатной плоскости, удовлетворяющих уравнению:
х-у+2=0
(х+4)2+(у-1)2=9
Решение
х-у+2=0 Данное множество точек, расположено на прямой у=х+2

(х+4)2+(у-1)2=9 Данное множество точек, расположено на окружности с центром в точке О(-4;1) и радиусом R=3

Найти множество точек координатной плоскости, удовлетворяющих неравенству:
2х+у-1≤0
х2+(у-2)2<4
Решение
2х+у-1≤0
Строим заданную прямую и укажем штриховкой множество точек, удовлетворяющих заданным условиям. Множество точек, расположенных на прямой, также включается в область

х2+(у-2)2<4 Данное множество точек лежит внутри круга с центром в точке
О (0; 2) и радиусом R=4. Ободок окружности не включается в заданную область

Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств

Решение
Изобразим в одной системе координат прямые
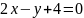 (график
красного цвета)
(график
красного цвета)
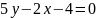 (график
синего цвета)
(график
синего цвета)

Найдем пересечение (общую часть) областей, которым соответствуют указанные неравенства

