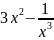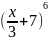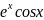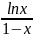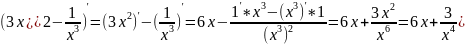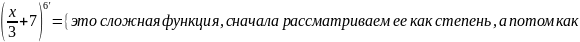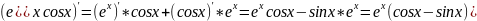Оглавление

Контрольная работа №1² 2

Контрольная работа №2 3

Контрольная работа №3 6

Контрольная работа №4 8

Контрольная работа №5 9

Контрольная работа №6 10

Контрольная работа №8 12

Контрольная работа № 5.1 15

Контрольная работа № 6.1 16

Контрольная работа № 7.1 19

Контрольная работа №12

Базовый уровень

1. Найти область определения и множество значений функции y=sinx+2

Решение

Область определения D(y)=R – функция определена на всей числовой оси

Чтобы найти множество значений функции, выразим х через у:

Sinx=у-2х=arcsin(y-2) -1≤y-2≤1 (т.к. функция арксинус принимает значения именно в этом диапазоне) 1≤у≤3 (просто упрощаем двойное неравенство)

2. Выяснить, является ли функция Y=x²+cosx четной или нечетной

Решение

Шаг 1. Находим область определения функции: D(y)=R

Шаг 2. Проверяем симметричность области определения функции относительно нуля (выполняется)

Шаг 3. Находим у(-х)

у(-х)=(-х)²+ cos(-x)  у(-х)= х²+ cosx=у(х) – функция четная, т.к. выполняется условие у(-х)=у(х)

3. Доказать, что наименьший положительный период функции Y=cos2x равен π

Решение

Применим правило: если функция f периодическая и имеет период Т, то функция y=Af(kx+b) где A, k и  b постоянны, а  k≠0, также периодическая, причем, ее период T_o=T/|k|. 

У нас Т=2π — это наименьший положительный период функции косинуса, k=2

Находим: T_o=2π/2=π

4. Найти все принадлежащие отрезку [-π;π] корни уравнения sinx= 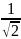с помощью графика функции

Решение

Построим графики функции у=sinx (синий) и у=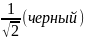 . Для нахождения корней уравнения, опустим перпендикуляры (красные) из точек пересечения графиков на ось ох. В указанный отрезок попадают только 2 корня. Это будут точки х=π/4 и х= π-π/4=3π/4

5. Построить график функции у=sinx-1 и найти значения аргумента, при которых функция возрастает, принимает наибольшее значение

Решение

Построим график функции у=sinx-1

Функция возрастает, если хє[-π/2+2πn; π/2+2πn], nєZ

Функция принимает наибольшее значение y=0 при х=π/2+2πn, nєZ

Контрольная работа №2

Базовый уровень

1. Найти производную функции:

1. 

2. 

3. 

4. 

Решение

1. 

2. 

3. 

4. 

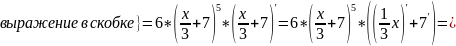
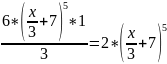
2. Найти значение производной функции y=f(x) в точке x₀, если

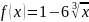x₀=8

Решение

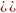
3. Записать уравнение касательной к графику функции f(x)=sinx-3x+2 в точке x₀=0

Решение

Уравнение касательной к графику функции y = f(x) в точке   имеет вид  .

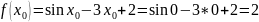
Уравнение касательной к графику функции f(x)=sinx-3x+2 в точке x₀=0 имеет вид

У=-2*(х-0)+2

У=-2x+2

4. Найти значения х, при которых значения производной функции положительны

Решение

Находим производную функции

Как видим, из найденной производной, ее знаменатель всегда будет числом положительным и в ноль никогда не обратится. Поэтому значения х, удовлетворяющие условию, следует искать только среди значений, которые принимает числитель дроби.

-(х²+2х-3)>0 х²+2х-3<0 (x+3)*(x-1)<0

Как видим, для нашего случая хє(-3;1)

5. Найти точки графика функции f(x)=x³-3x², в которых касательная к нему параллельна оси абсцисс

Решение

Найдем производную функции

Чтобы касательная к графику функции параллельна оси абсцисс, когда

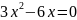
х(3х-6)=0

х=0 или 3х-6=0

х=0 или 3х=6

х=0 или х=2

Чтобы узнать ординату, подставляем значения х в саму функцию f(x)=x³-3x²

х=0 f(x)=0

х=2 f(x)=2³-3*2²=-4

Таким образом, это точки (0;0), (2;-4)

Контрольная работа №3

Базовый уровень