Алгоритм Флойда

5

4.3. Нахождение кратчайшего пути в орграфе

Рассмотрим ориентированный взвешенный граф D(V, A). Задача о кратчайшем пути состоит в отыскании пути минимального веса, соединяющего указанную начальную вершину графа D и все остальные вершины при условии, что хотя бы один такой путь существует.

4.3.1. Алгоритм Дейкстры

Данный алгоритм можно использовать в тех случаях, когда веса всех дуг неотрицательны.

Определим весовую матрицу W, чьи элементы задаются формулой

Обозначим через s начальную вершину орграфа, от которой нужно найти кратчайшие пути до всех остальных вершин.

В течение работы алгоритма каждой вершине v орграфа присваивается число d[v], равное расстоянию от s до v.

4.3.2. Алгоритм Флойда

Рассмотрим более общую ситуацию. Будем считать, что в графе D допускаются дуги отрицательного веса. Опишем алгоритм кратчайших путей между всеми парами вершин графа при условии, что в графе нет отрицательных контуров, т.е. замкнутых путей отрицательного веса. Если в графе D есть цикл с отрицательным весом, то решения поставленной задачи не существует, т.к. можно «накручивать» на этом цикле сколь угодно короткий путь.

Определим весовую матрицу W, чьи элементы w_ij задаются формулой

В алгоритме используются матрицы W⁰,…,Wⁿ и Р⁰,…,Р^п. Матрица W^k содержит веса кратчайших путей, проходящих только через вершины 1,2,…,k. В матрице P^k элемент - номер вершины, предшествующий вершине j в текущем (i, j)-пути.

Рассмотрим алгоритм.

1. W⁰=W; k:=1; Р⁰=[],

где

2. выполнить: если , то ; . Иначе ; .

3. Если для некоторого , (по диагонали матрицы W^k появляются отрицательные значения), то конец (в графе имеется отрицательный контур). Иначе перейти к пункту 4.

4). . Если , то конец. – матрица весов кратчайших путей. С помощью матрицы кратчайший -путь определяется следующим образом:

,

Иначе перейти к пункту 2.

Пример.

Рассмотрим нагруженный граф D(V, А).

Рис. Орграф D с отрицательными весами.

Составим матрицу весов W⁰ и матрицу путей между парами вершин P⁰

,

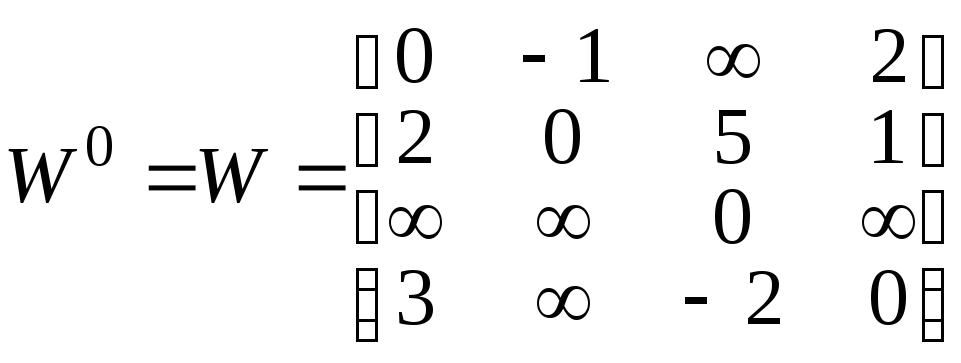k=1. Если , то ; .

Иначе ; .

 - неравенство выполняется,  - неравенство не выполняется.

i=1	j=1	0 ≤ 0+0		i=2	j=1	2 ≤ 2+0	
	j=2	–1 ≤ 0+(–1)			j=2	0 ≤ 2+(–1)	
	j=3	 ≤ 0+			j=3	5 ≤ 2+	
	j=4	2 ≤ 0+2			j=4	1 ≤ 2+2	
i=3	j=1	 ≤ +0		i=4	j=1	3 ≤ 3+0	
	j=2	 ≤ +(–1)			j=2	 ≤ 3+(–1)	
	j=3	0 ≤ +			j=3	–2 ≤ 3+	
	j=4	 ≤ +2			j=4	0 ≤ 3+2	

; ;

, .

k=2. Если , то ; .

Иначе ; .

i=1	j=1	0 ≤ –1+2		i=2	j=1	2 ≤ 0+2	
	j=2	–1 ≤ –1+0			j=2	0 ≤ 0+0	
	j=3	 ≤ –1+5			j=3	5 ≤ 0+5	
	j=4	2 ≤ –1+1			j=4	1 ≤ 0+1	
i=3	j=1	 ≤ +2		i=4	j=1	3 ≤ 2+2	
	j=2	 ≤ +0			j=2	2 ≤ 2+0	
	j=3	0 ≤ +5			j=3	–2 ≤ 2+5	
	j=4	 ≤ +1			j=4	0 ≤ 2+1	

; ;

; ;

, .

k=3. Если , то ; . Иначе ; .

i=1	j=1	0 ≤ 4+		i=2	j=1	2 ≤ 5+	
	j=2	–1 ≤ 4+			j=2	0 ≤ 5+	
	j=3	4 ≤ 4+0			j=3	5 ≤ 5+0	
	j=4	0 ≤ 4+			j=4	1 ≤ 5+	
i=3	j=1	 ≤ 0+		i=4	j=1	3 ≤ –2+	
	j=2	 ≤ 0+			j=2	2 ≤ –2+	
	j=3	0 ≤ 0+0			j=3	–2 ≤ –2+0	
	j=4	 ≤ 0+			j=4	0 ≤ –2+	

Весовая матрица и матрица путей остаются без изменений.

, .

k=4. Если , то ; .

Иначе ; .

i=1	j=1	0 ≤ 0+3		i=2	j=1	2 ≤ 1+3	
	j=2	–1 ≤ 0+2			j=2	0 ≤ 1+2	
	j=3	4 ≤ 0+(–2)			j=3	5 ≤ 1+(–2)	
	j=4	0 ≤ 0+0			j=4	1 ≤ 1+0	
i=3	j=1	 ≤ +3		i=4	j=1	3 ≤ 0+3	
	j=2	 ≤ +2			j=2	2 ≤ 0+2	
	j=3	0 ≤ +(–2)			j=3	–2 ≤ 0+(–2)	
	j=4	 ≤ +0			j=4	0 ≤ 0+0	

; ;

; ;

, .

Итак, найдена матрица весов кратчайших путей и матрица кратчайших путей между парами вершин.

Определим маршрут и вес пути Р(1, 4). Вершины v₁=1 и v₂=4 соединены дугой веса d=2. Однако

, где . И в этом случае вес пути .

Определим маршрут и вес пути Р(1, 3). Дуга (1, 3) в данном графе отсутствует.

, где . Вес пути .

Пример.

Рассмотрим нагруженный граф D(V, А).

Рис. Орграф D с отрицательными весами.

Матрица весов W⁰ и матрица путей между парами вершин P⁰

,

k=1	i=1	j=1	0 ≤ 0+0		i=2	j=1	6 ≤ 6+0	
		j=2	 ≤ 0+			j=2	0 ≤ 6+	
		j=3	3 ≤ 0+3			j=3	–5 ≤ 6+3	
		j=4	 ≤ 0+			j=4	–2 ≤ 6+	
	i=3	j=1	 ≤ +0		i=4	j=1	2 ≤ 2+0	
		j=2	2 ≤ +			j=2	 ≤ 2+	
		j=3	0 ≤ +3			j=3	 ≤ 2+3	
		j=4	–1 ≤ +			j=4	0 ≤ 2+	

; ;

,

k=2	i=1	j=1	0 ≤ +6		i=2	j=1	6 ≤ 0+6	
		j=2	 ≤ +0			j=2	0 ≤ 0+0	
		j=3	3 ≤ +(–5)			j=3	–5 ≤ 0+(–5)	
		j=4	 ≤ +(–2)			j=4	–2 ≤ 0+(–2)	
	i=3	j=1	 ≤ 2+6		i=4	j=1	2 ≤ +6	
		j=2	2 ≤ 2+0			j=2	 ≤ +0	
		j=3	0 ≤ 2+(–5)			j=3	5 ≤ +(–5)	
		j=4	–1 ≤ 2+(–2)			j=4	0 ≤ +(–2)	

; ;

. Таким образом, в графе существует контур (замкнутый путь) отрицательного веса. Следовательно, на этом работа алгоритма закончена.