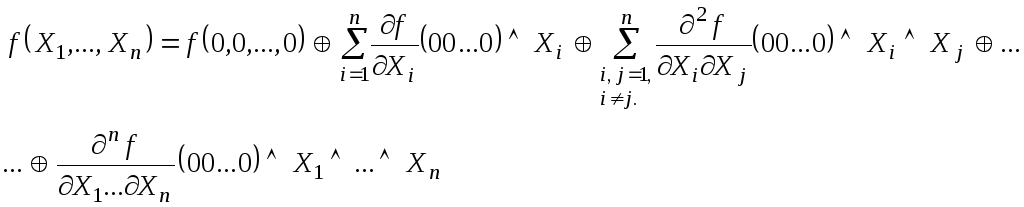1. Контрольные вопросы для самостоятельной подготовки к экзамену (79 баллов)

1. Поиск в глубину.

2. Поиск в ширину.

3. Алгоритм Краскала.

4. Алгоритм Прима.

5. Алгоритм Дейкстра.

6. Алгоритм Флойда.

7. Поток в транспортной сети.

8. Алгоритм нахождения полного потока в транспортной сети.

9. Орграф приращений.

10. Разрез. Пропускная способность разреза.

11. Алгоритм нахождения максимального потока в транспортной сети.

12. Высказывание. Логические операции. Приоритет операций. Формулы алгебры высказываний.

13. Равносильность формул.

14. Закон двойственности.

15. Тождественно истинные и ложные формулы.

16. Нормальные формы.

17. Совершенные нормальные формы.

18. Представление булевой функции формулой алгебры высказывания. Таблицы истинности.

19. Алгебра Жегалкина.

20. Дифференцирование булевых функций.

21. Разложение булевой функции в заданной точке пространства.

22. Теорема о функциональной полноте (теорема Поста). Примеры функционально-полных базисов.

23. Минимизация функций аналитическим путем.

24. Карты Карно.

25. Метод Квайна – Мак-Класски.

26. Схемы из функциональных элементов.

27. Понятие конечного автомата. Автоматы Мили и Мура.

28. Способы задания конечного автомата.

29. Расширение функций переходов и выходов на множество входных слов.

30. Автоматное отображение.

31. Представление конечных автоматов матрицами соединений.

32. Дерево конечного автомата.

33. Основные формулы комбинаторики.

34. Биномиальные коэффициенты. Бином Ньютона.

35. Алфавитное кодирование. Таблица кодов.

36. Кодирование с минимальной избыточностью.

37. Коды с обнаружением и исправлением ошибок.

38. Целые числа и полиномы.

39. Рекуррентные уравнения.

2. Список теорем, необходимых для сдачи экзамена (10 баллов)

Утверждение 5.2. Для любого допустимого потока  в транспортной сети D и любого множества V₁V, где v₁V₁, v_nV₁, выполняется неравенство , т.е. величина любого допустимого потока в сети D (в том числе и максимального) не превышает пропускной способности любого разреза сети (в том числе и минимального).

Теорема 5.1 (теорема Форда-Фалкерсона). Пусть D – транспортная сеть,  – допустимый поток в этой сети, V₁ – множество вершин vV таких, что длина минимального пути из v в v_n в орграфе приращений I(D, ) равна нулю. Тогда, если v₁V₁, то  – максимальный поток, величина которого равна .

Теорема 6.2 (о приведении к ДНФ). Для любой формулы А можно найти такую формулу В, находящуюся в ДНФ, что . Формула В называется дизъюнктивной нормальной формой формулы А.

Доказательство. Доказательство теоремы распадается на три этапа.

1). Для формулы А строим такую формулу , что и в не содержатся операции (равносильности 22 – 28).

2).Докажем теперь, что для формулы можно найти равносильную ей формулу такую, что и в операция отрицание находится только над переменными. Такая формула называется формулой с «тесными» отрицаниями. Докажем это утверждение индукцией по числу n логических символов (операций) формулы .

Если то есть какая-то переменная . В качестве нужно взять .

Пусть утверждение выполняется для всех формул с числом символов меньше n.

Пусть в формуле содержится n логических операций. Рассмотрим случаи.

а) имеет вид . Тогда в логических символов меньше, чем n. Поэтому существуют формулы такие, что и в отрицание встречается только над переменными. Отсюда и является формулой с «тесными» отрицаниями.

б) имеет вид . Доказательство аналогично предыдущему случаю.

в) имеет вид . Тогда (применили равносильность 11) и в логических операций меньше, чем n. Поэтому к применено индуктивное предположение.

г) имеет вид . Тогда (применили равносильность 13) и в логических символов меньше, чем n. Поэтому существуют формулы такие, что и в отрицание встречается только над переменными. Ясно, что и является формулой с «тесными» отрицаниями.

д) имеет вид . Тогда (применили равносильность 12) и далее поступаем, как и в предыдущем случае.

3). Полученную формулу можно считать построенной из переменных и их отрицаний с помощью многочленных конъюнкций и дизъюнкций. Применив теперь обобщённую дистрибутивность относительно , последовательно преобразуем формулу. Дизъюнкция () будет аналогична сложению, конъюнкция () – умножению. Полученная в результате преобразований формула В будет удовлетворять требованиям теоремы.

Теорема 6.3 (о приведении к КНФ). Для любой формулы А можно найти такую формулу В, находящуюся в КНФ, что Формула В называется конъюнктивной нормальной формой А.

Доказательство. Применив первые два этапа из доказательства теоремы 6.2 о ДНФ, получим формулу , равносильную А, не содержащую символов и содержащую отрицания только над переменными. Преобразуем теперь , применяя обобщенную дистрибутивность относительно . В результате получим формулу В, находящуюся в КНФ.

Теорема 6.4. Пусть формула А зависит от списка переменных () и А не тождественно-ложная формула. Тогда существует такая формула В, что и В находится в СДНФ относительно списка этих переменных.

Доказательство. Согласно теореме о приведении к ДНФ, существует формула такая, что и находится в ДНФ. При этом можно считать, что зависит от списка переменных (). Будем исходить из этой формулы, и просматривать её элементарные конъюнкции:

1. Пусть в элементарную конъюнкцию одновременно входит какая-нибудь переменная и её отрицание . Если это единственная элементарная конъюнкция, то она на всех значениях переменной принимает значение Л, а, следовательно, и вся формула, что невозможно, так как предполагается, что формула не тождественно-ложная.

Следовательно, имеются другие элементарные конъюнкции, и формула (после некоторых перестановок) будет иметь вид: ,

где С – остальные члены нашей элементарной конъюнкции, D – остальные дизъюнктивные члены всей формулы.

Но поскольку , то . Следовательно, рассматриваемую конъюнкцию можно отбросить.

Так как А не тождественно-ложная, то после всех таких шагов всегда останутся какие-то неотброшенные элементы конъюнкции.

2. Пусть в некоторой элементарной конъюнкции переменная (или ) встречается несколько раз. Тогда в силу идемпотентности (равносильность 5), можно оставить только одно вхождение(или ).

3. После проведенной обработки каждая элементарная конъюнкция С будет содержать какую-нибудь переменную не более одного раза (включая её вхождение под знаком отрицания). При этом возможны только следующие варианты:

а) элементарная конъюнкция С содержит один раз и не содержит ни разу;

б) элементарная конъюнкция С содержит один раз и не содержит ни разу;

в) элементарная конъюнкция С не содержит ни, ни .

В последнем случае мы заменяем С на по первой формуле расщепления (равносильность 14). Эту операцию следует проводить до тех пор, пока для каждой элементарной конъюнкции и каждой переменной не будут выполнены условия а) или б).

4. Переупорядочим в каждой элементарной конъюнкции её члены таким образом, чтобы на i-ом месте в ней стояла или .

5. Если в преобразованной формуле несколько раз встречается одна и та же элементарная конъюнкция, то, пользуясь равносильностью 6 (идемпотентность ), выбрасываем все её вхождения, кроме одного.

Теорема 6.6. Пусть формула А зависит от списка переменных () и А не тождественно-истинная. Тогда существует такая формула В, что и В находится в СКНФ относительно списка этих переменных.

Доказательство. Доказательство аналогично доказательству теоремы 6.4.

Теорема 6.9 (о разложении функции по переменным). Каждую булеву функцию при любом k (1 ≤ k ≤ п) можно представить в следующей форме

, (6.7)

где дизъюнкция берется по всевозможным наборам значений переменных .

Доказательство. Рассмотрим произвольный набор значений переменных и покажем, что левая и правая части соотношения (6.7) принимают на нем одно и то же значение.

Левая часть .

Правая часть

как только хотя бы один из сомножителей будет равен нулю, вся конъюнкция обратится в нуль. Таким образом, из ненулевых конъюнкций останется лишь та, в которой и

в силу того, что , получаем

.

Следствие 6.1. Разложение произвольной булевой функции по одной переменной имеет вид

.

Функции и называются компонентами разложения.

Теорема 6.10 (о СДНФ булевой функции). Для любой булевой функции , отличной от константы 0, справедливо следующее представление

.

Доказательство. Пусть функция отлична от константы 0. Напишем разложение этой функции по k = n переменным

,

что можно переписать в эквивалентном виде, согласно следствию 6.1.

.

Учитывая, что в первой дизъюнкции все значения функции равны 1, а вторая обнуляется из-за того, что все значения функции в ней равны 0, получаем утверждение теоремы, т.е.

.

Такое разложение носит название совершенной дизъюнктивной нормальной формы булевой функции.

Теорема 6.11 (о СКНФ булевой функции). Для любой булевой функции , отличной от константы 1, справедливо следующее представление

.

Доказательство. Запишем СДНФ для двойственной функции, т.е.

По тождеству для двойственных формул получаем

Левая часть .

Правая часть

.

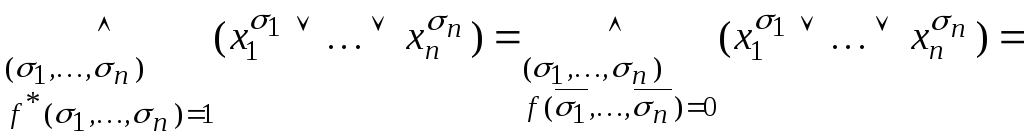
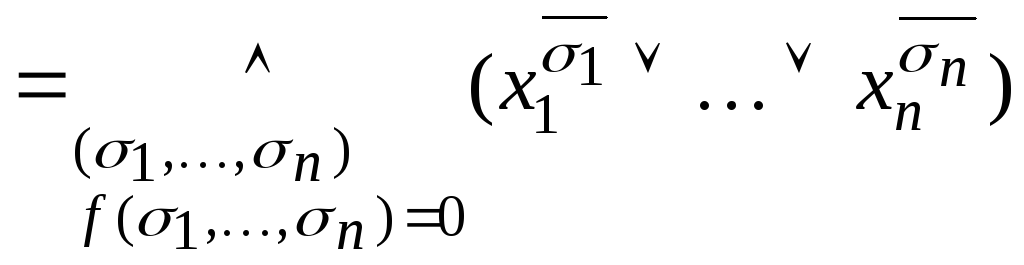Такое разложение носит название совершенной конъюнктивной нормальной формы булевой функции.

Теорема 6.13. Любая булева функция представима своим значением в точке (00…0) и значениями всех производных в этой точке в виде:

5