Лабораторная работа №6 Решение нелинейных уравнений методом итерации
Краткая теория
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Требуется найти этот корень с точностью ε. Для уточнения корня методом итерации приведем уравнение (1) к виду :
(2)
Построим итерационную последовательность приближений к корню следующим образом:
выберем произвольно,
(3)
Сходимость метода
Можно доказать,
что если эта последовательность
сходится, то она сходится к корню
уравнения (2), а значит, и уравнения (1).
Последовательность (3) сходится, если
является сжимающим отображением отрезка
[a,b]
в себя, что равносильно ограниченности
модуля производной
:
для всех
.
Погрешность метода
Метод итерации
обеспечивает на n-м
шаге абсолютную погрешность приближения
к корню уравнения (1), не превосходящую
длины n-го
отрезка, умноженной на дробь
:
,
где
.
Чтобы функция
обеспечивала
сходимость последовательности (3), она
должна иметь вид
,
где
знак
k
совпадает со знаком f’(x)
на [a,b].
(4)
Алгоритм метода
Найти f’(x), ее знак и Q-наибольшее значение ее модуля на [a,b].
Выбрать число k, отвечающее условию (4).
Построить функцию , убедиться что <1.
Найти величину
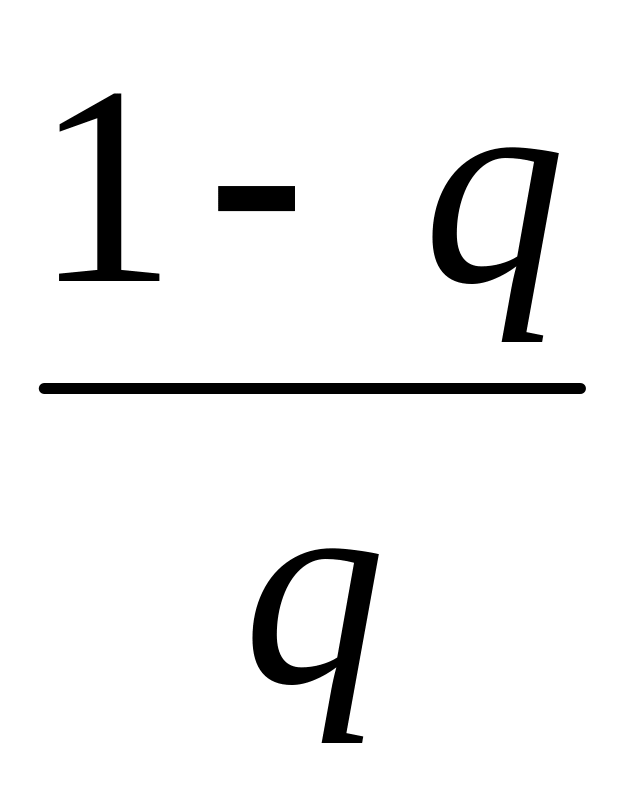ε.Взять произвольно, например один из концов отрезка [a,b].
Вычислять значения до выполнения условия
Р
ешение
одного варианта
Отделить корни, уточнить их методом итерации с точностью до 0,001:
.
Отделим корни графически (см.рис.).
Уравнение имеет
один действительный корень:
Уточним корень методом итерации:
n
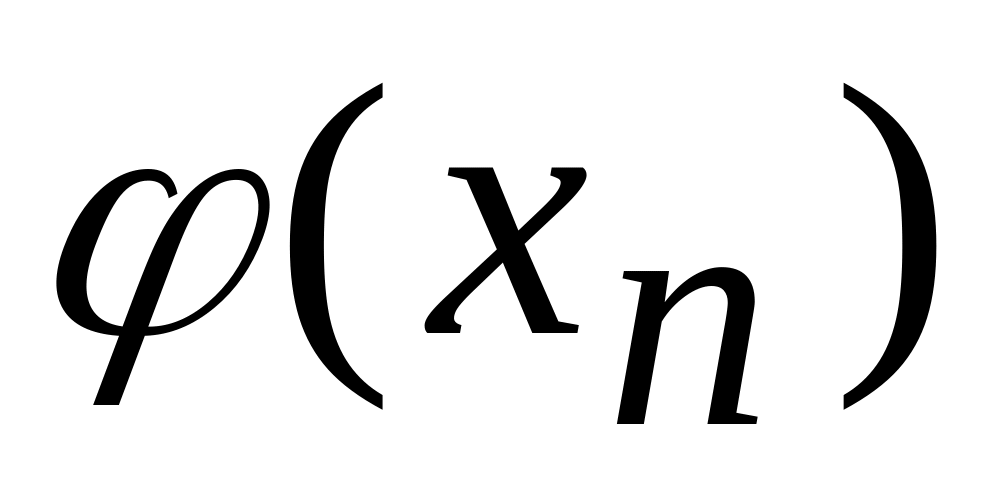
0
-1,0000
-0,3420
1
-0,3420
-0,4511
2
-0,4511
-0,4856
3
-0,4856
-0,4929
4
-0,4929
-0,4942
5
-0,4942
-0,4944
6
-0,4944
-0,4945
Выберем k=-4.
;
;
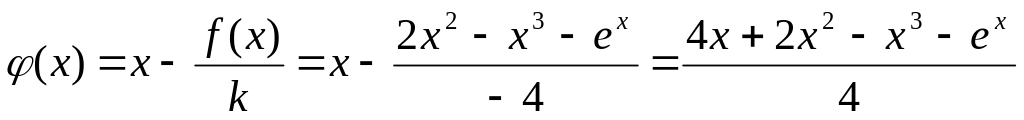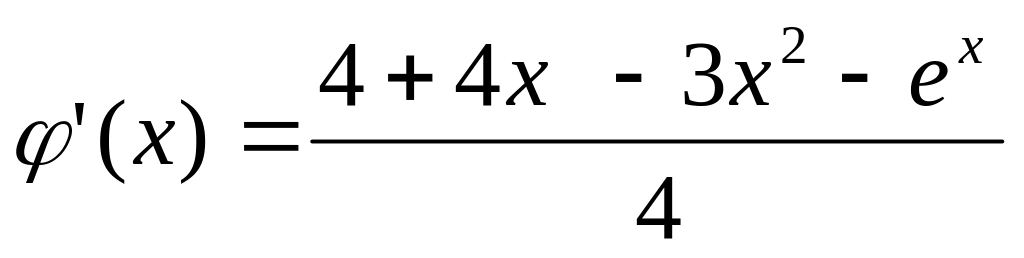q=0,84<1, ε=
.За примем левый конец отрезка -1.
Вычисления занесем в таблицу:
Поскольку
,
считаем, что корень уравнения
.
Задание
Решить уравнение методом итерации с точностью до 0,001.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25. 10cosx-0,1x2=0
26.
27.
28. lg(x+5)=cosx