Лабораторная работа №5 Решение нелинейных уравнений комбинированным методом хорд и касательных
Краткая теория
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Объединяя методы хорд и касательных, получим метод, дающий на каждом шаге сразу два приближения к корню- по недостатку и по избытку (рис.1).
Здесь ξ – точный
корень уравнения (1),
и
- начальные приближения к корню по
недостатку и по избытку соответственно,
и
- точки пересечения касательной и хорды
с осью Ох
– первые приближения к корню. Далее
комбинированный метод применяется на
отрезке [
;
].
В случае, изображенном на рис.1, удобно
слева проводить касательную, а справа
– хорду. Для вычисления новых приближений
применяется формула, обозначим её (2):
(2)
В случае, если слева проводится хорда, а справа касательная, применяются формулы:
(3)
Правило выбора формул
Если знаки первой и второй производной функции f(x) на отрезке [a,b] совпадают, то применяются формулы (3), если разные - формулы (2).
Погрешность метода
Метод хорд и касательных обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1) , не превосходящую длины n-го отрезка:
Алгоритм метода
Определить, какую пару формул ((2) или (3)) выбрать. Принять ,
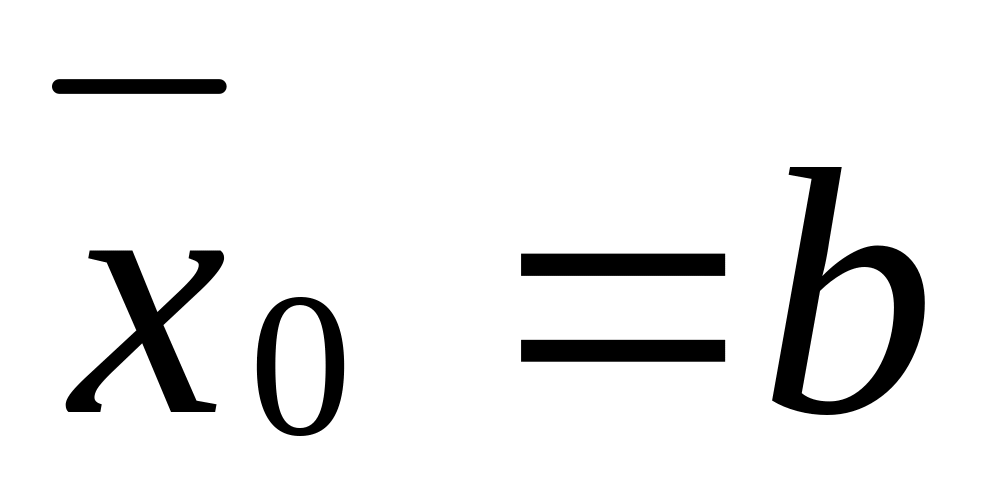.Вычислить два новых приближения к корню
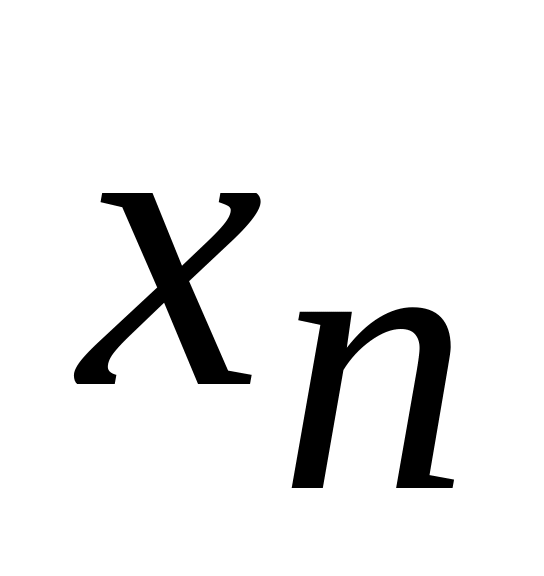и
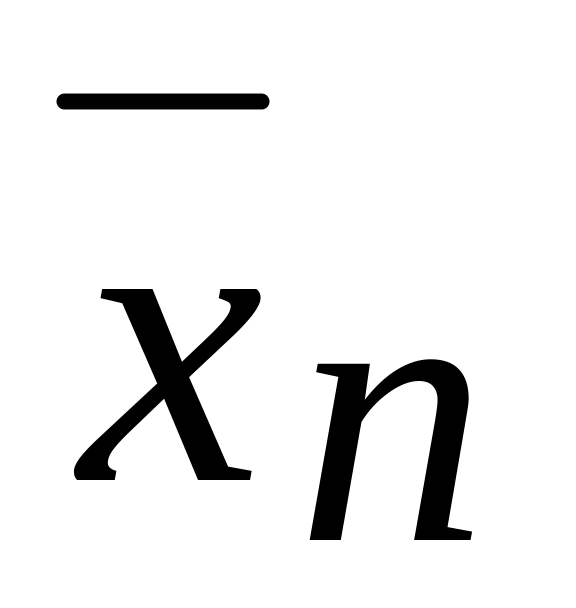по формуле (2) или (3).Если длина отрезка [
]
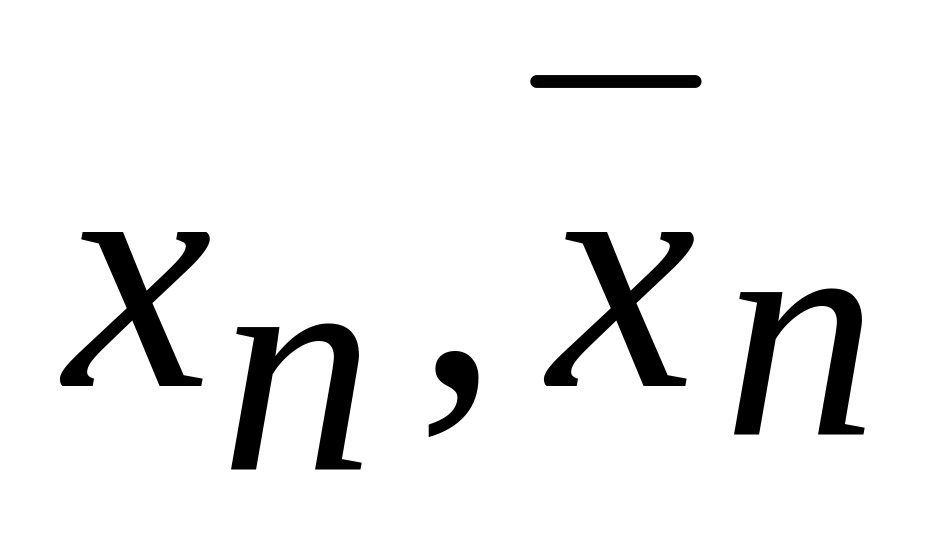не превосходит заданной точности, то
процесс заканчивается и в качестве
точного корня можно взять
или
,
иначе идти к п.2.
Решение одного варианта
Отделить корни и
уточнить их комбинированным методом
с точностью до 0,001:
.
Отделим корни аналитически. Находим
;
.
D= 16+48=64.
,
.
Составим таблицу
знаков функции
х |
|
|
2 |
|
знак f(x) |
- |
+ |
- |
+ |
Уравнение имеет
три действительных корня:
;
Уменьшим промежутки, содержащие корни, до единичной длины:
х |
-2 |
-1 |
0 |
1 |
2 |
3 |
знак f(x) |
- |
+ |
+ |
+ |
- |
+ |
Следовательно,
.
Уточним корни комбинированным методом:
1.
.
Для вычислений применяем формулы
(2)
Полагаем
,
Все вычисления производим в таблице, обозначив
;
n |
|
|
|
|
|
|
|
|
|
||||
0 |
-2 |
1 |
-1 |
16 |
9 |
-0,0625 |
-1 |
8 |
0,08889 |
||||
1 |
-1,9375 |
0,0486 |
-0,031 |
15,0117 |
0,7112 |
-0,0021 |
-1,8889 |
0,6802 |
0,0465 |
||||
2 |
-1,9354 |
0 |
0,0005 |
|
|
|
-1,9354 |
0,0005 |
2.
.
Для вычисления
применяем те же формулы , полагая
.
Вычисления производим в таблице:
n |
|
|
|
|
|
|
|
|
|
||||
0 |
1 |
1 |
2 |
-5 |
-3 |
-0,4 |
2 |
-1 |
0,333 |
||||
1 |
-1,4 |
0,267 |
0,224 |
-3,72 |
-0,817 |
-0,06 |
-1,667 |
-0,593 |
0,194 |
||||
2 |
1,46 |
0,013 |
0,009 |
-3,4452 |
-0,044 |
-0,003 |
1,473 |
-0,035 |
0,01 |
||||
3 |
1,463 |
0 |
-0,001 |
|
|
|
1,463 |
-0,001 |
.
3.
Для вычисления применяем формулы
,
где
Вычисления производим в таблице, обозначив
.
n |
|
|
|
|
|
|
|
|
|
||||
0 |
2 |
1 |
-1 |
11 |
5 |
-0,2 |
|
4 |
0,364 |
||||
1 |
2,2 |
0,436 |
-0,832 |
6,301 |
1,707 |
-0,212 |
2,636 |
0,875 |
0,139 |
||||
2 |
2,412 |
0,085 |
-0,251 |
4,717 |
0,362 |
-0,259 |
2,497 |
0,11 |
0,023 |
||||
3 |
2,471 |
0,003 |
-0,008 |
4,466 |
0,013 |
-0,002 |
2,474 |
0,005 |
0,001 |
||||
4 |
2,473 |
0 |
0,0007 |
4,455 |
|
|
2,473 |
.
Задание
Решить уравнение комбинированным методом с точностью до 0,001
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
