Лабораторная работа №4 Решение нелинейных уравнений методом касательных
Краткая теория
Будем рассматривать
уравнение вида
(1).
Пусть корень
уравнения отделен и находится на отрезке
[a,b].
Уточним этот корень методом касательных.
Геометрически метод касательных
означает замену на отрезке
графика функции
касательной, проведенной через точку
или
:
Здесь
-
точный корень уравнения (1) ,
-
начальное приближение к корню,
-
точка пересечения касательной с осью
Оx
– первое приближение к корню. Далее
метод касательных применяется на
отрезке
и получается второе приближение корню
-
.
В случае, изображенном на рис.1, конец
отрезка а принимает за начальное
приближение к корню и касательная
каждый раз проводится через левый конец
отрезка. Из уравнения касательной и
условия, что точка
принадлежит касательной, получается
формула для вычисления n-го
приближения к корню:
,
(2)
Правило определения начального приближения к корню
За начальной приближение принимается тот конец отрезка, в котором знак функции совпадает со знаком её второй производной на отрезке [a,b].
Погрешность метода
Метод касательных обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длины n-го отрезка:
Алгоритм метода
Определить, какой конец отрезка принять за .
Вычислить новое приближение к корню по формуле (2).
Если длина отрезка
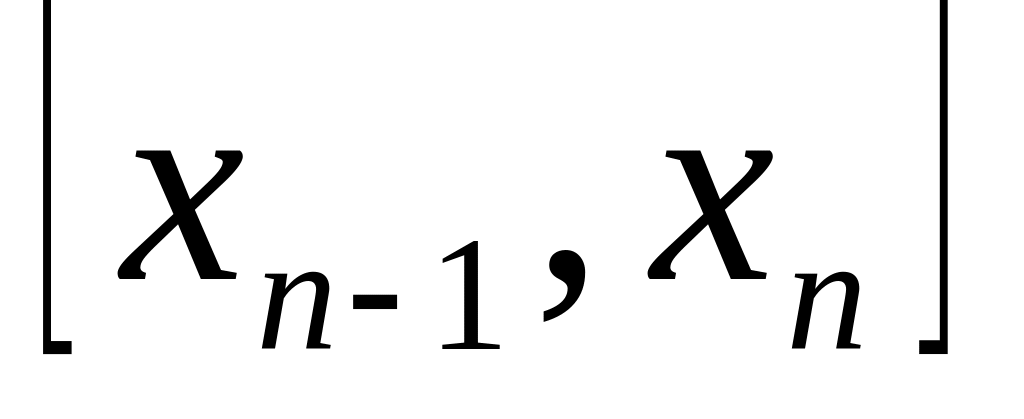не превосходит заданной точности, то
процесс заканчивается и в качестве
точного корня можно взять
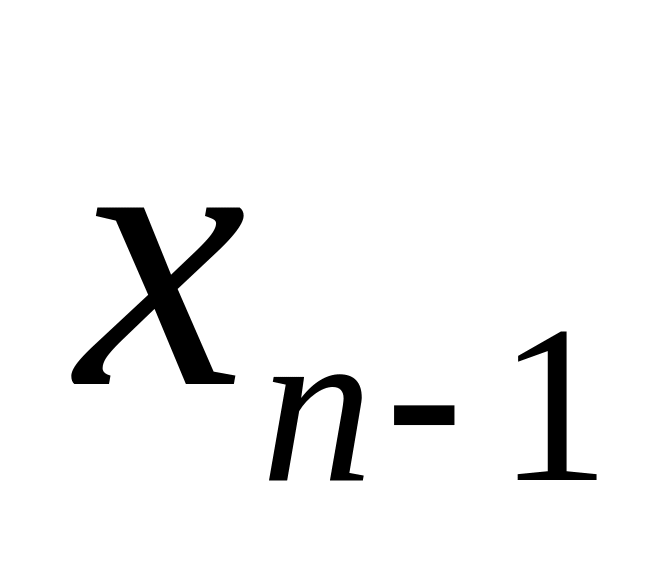или
,
иначе идти к п.2.
Решение одного варианта
1. Отделить корни графически и уточнить их методом касательных с точностью до 0.001:
Отделим корень
графически. Построим графики функций
и
:
Таким образом,
уравнение имеет два корня
и
.
Чтобы уточнить
первый корень методом касательных,
определим знак второй производной
функции
на промежутке [0.5;1]. Имеем
;
при
;
,
;
следовательно,
за
следует
принять правый конец отрезка:
.
Для вычислений используем формулу (2).
Все вычисления удобно располагать в таблице:
n |
|
|
|
|
0 |
1 |
-0.2398 |
-1.1321 |
0.212 |
1 |
0.788 |
-0.1272 |
-0.9896 |
0.129 |
2 |
0.765 |
-0.0117 |
-0.7991 |
0.015 |
3 |
0.750 |
-0.0001 |
-0.7759 |
0 |
4 |
0.750 |
|
|
|
Второй корень
вычисляется по формуле (2) при
и равен -0.144.
Ответ: x ≈ 0.750, x ≈ -0.144
2.
Определить корни аналитически и уточнить
их методом касательных до 0.001:
.
Находим 
.
Составим таблицу знаков функции f(x):
x |
- ∞ |
-1 |
0 |
1 |
+ ∞ |
Знак f(x) |
- |
- |
+ |
+ |
+ |
Из таблицы видно, что уравнение имеет один действительный корень .
Уточним корень методом касательных.
,
,
при
В качестве
начального приближения возьмем
.
Для вычислений применяем формулу (2): , , где
Вычисления удобно располагать в таблице:
n |
|
|
|
|
0 |
-1 |
-0.2 |
3.9 |
-0.051 |
1 |
-0.949 |
-0.009 |
3.581 |
-0.003 |
2 |
-0.946 |
0.001 |
3.563 |
0 |
3 |
-0.946 |
|
|
|
4 |
|
|
|
|
Ответ.
.
Задания
Отделить корни графически и уточнить их методом касательных до 0.001
Отделить корни уравнения аналитически и уточнить их методом касательных до 0.001:
