Лабораторная работа №11 Обработка экспериментальных данных
Краткая теория
Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f: f(x0)=y0, f(x1)=y1,…, f(xn)=yn. Нужно найти формулу, выражающую эту зависимость аналитически. Интерполяционные многочлены, хотя и гарантируют точное совпадение значений в узлах, не обеспечивают совпадения характера поведения исходной и интерполирующей функций. Потребуем, чтобы приближающая функция y=F(x) (1) принимала в точках x0,x1,…,xn значения, как можно более близкие к табличным значениям y0,y1,…,yn. Один из способов нахождения формулы (1) носит название метода наименьших квадратов.
Метод наименьших квадратов
Пусть функция F в точках x0,x1,…,xn имеет значения F(x0),F(x1),…,F(xn) (2). Требование близости табличных значений y0,y1,…,yn и значений (2) равносильно следующему: сумма квадратов
S=(y0-F(x0))2+(y1-F(x1))2+…+(yn-F(xn))2 (3)
должна быть наименьшей.
В качестве приближающих функций в зависимости от характера точечного графика функции f часто используют следующие функции:
F(x)=a1x+a0 5) F(x)=1/(cx+m)
F(x)=a2x2+a1x+a0 6) F(x)=clnx+m
F(x)=cxm 7) F(x)=c/x+m
F(x)=cemx 8) F(x)=x/(cx+m)
Для нахождения коэффициентов a0 и a1 линейной функции из условия (3) получается система двух линейных уравнений:
,
где
,
(4)
Коэффициенты квадратичной функции a0, a1, a2 находятся из аналогичной системы
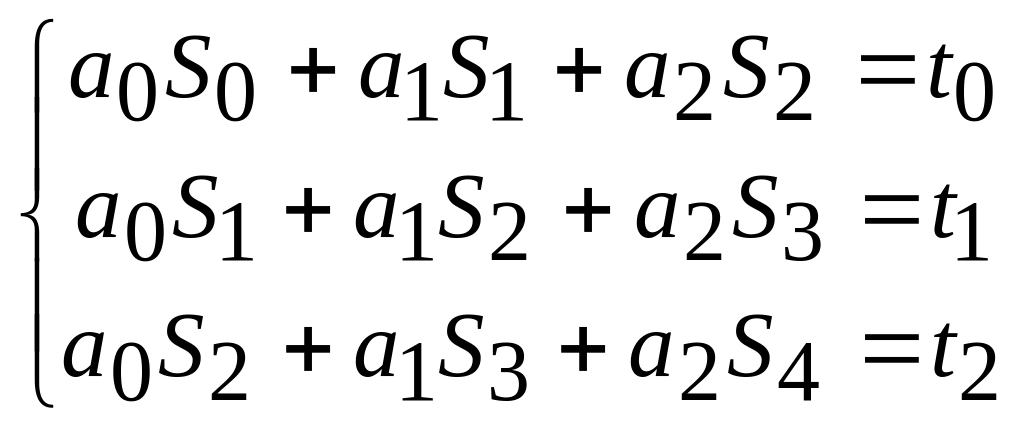при тех же
обозначениях Sk
и tk
(5)
Нахождение приближающих функций вида 3)-8) сводится к нахождению линейной функции (u)=a1u+a0 путем ввода новой переменной u по следующим правилам:
Вид функции F(x) |
Вид переменной u и функции (u) |
Преобразование исходной таблицы |
Выражения c и m через a0 и a1 |
F(x)=cxm |
u=ln x (u)=lnF(x) |
xlnx; ylny |
c=exp(a0); m=a1 |
F(x)=cemx |
u=x; (u)=lnF(x) |
x не меняется ylny |
c=exp(a0); m=a1 |
F(x)=1/(cx+m) |
U=x; (u)=1/F(x) |
x не меняется y1/y |
c=a1; m=a0 |
F(x)=cln x+m |
u=lnx; (u)=F(x) |
x lnx; y не меняется |
c=a1; m=a0 |
F(x)=c/x+m |
u=1/x; (u)=F(x) |
x1/x; y |
c=a1; m=a0 |
F(x)=x/(cx+m) |
u=1/x; (u)=1/F(x) |
x1/x; y1/y |
c=a0; m=a1 |
Решение одного варианта
По заданной таблице значений x и y, полученных экспериментально, построить методом наименьших квадратов две различные эмпирические формулы и сравнить качество полученных приближений
x |
1.1 |
1.7 |
2.4 |
3.0 |
3.7 |
4.5 |
5.1 |
5.8 |
y |
0.3 |
0.6 |
1.1 |
1.7 |
2.3 |
3.0 |
3.8 |
4.6 |
Точечный график изображен на рисунке:
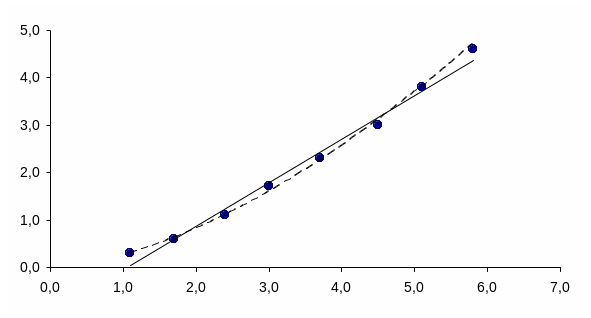
Составим теперь
систему вида (4):
,
где
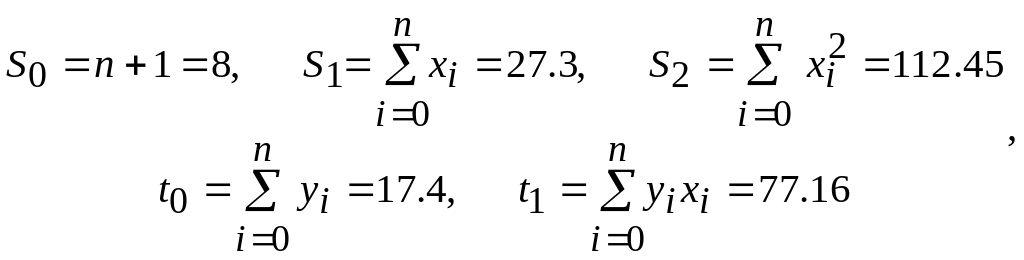
Решив систему, получаем: a0=-0.968, a1=0.921. Приближающая функция имеет вид:
F1(x)=0.921x -0.968 (6)
Для нахождения коэффициентов c и m степенной функции обозначим новые переменные u и (u), т.е. u=lnx, (u)=lnF(x), (u)=lnc+mu=a0+a1u. По исходной таблице составляется новая таблица из логарифмов значений x и y:
|
u |
(u) |
u(u) |
u2 |
|
0,095 |
-1,204 |
-0,114 |
0,009 |
|
0,531 |
-0,511 |
-0,271 |
0,282 |
|
0,875 |
-0,095 |
-0,083 |
0,766 |
|
1,099 |
0,531 |
0,584 |
1,208 |
|
1,308 |
0,833 |
1,090 |
1,711 |
|
1,504 |
1,099 |
1,653 |
2,262 |
|
1,629 |
1,335 |
2,175 |
2,654 |
|
1,758 |
1,526 |
2,683 |
3,091 |
|
8,799 |
3,514 |
7,715 |
11,981 |
По числовым данным из новой таблицы составляется система уравнений вида (4):
Ее решения a1=1.671, a0=-1.399.
Находим значения параметров c и m: m=1.671, c=exp(-1.399)=0.247.
Приближающая функция имеет вид
F2(x)=0.247x1.671 (7)
Для сравнения качества приближений (6) и (7) вычислим суммы квадратов отклонений:
x |
y |
F1(x) |
1 |
12 |
F2(x) |
2 |
22 |
1,1 |
0,3 |
0,0451 |
0,2549 |
0,0650 |
0,2894 |
0,0106 |
0,0001 |
1,7 |
0,6 |
0,5977 |
0,0023 |
0,0000 |
0,5991 |
0,0009 |
0,0000 |
2,4 |
1,1 |
1,2424 |
-0,1424 |
0,0203 |
1,0662 |
0,0338 |
0,0011 |
3 |
1,7 |
1,795 |
-0,095 |
0,0090 |
1,5483 |
0,1517 |
0,0230 |
3,7 |
2,3 |
2,4397 |
-0,1397 |
0,0195 |
2,1984 |
0,1016 |
0,0103 |
4,5 |
3 |
3,1765 |
-0,1765 |
0,0312 |
3,0493 |
-0,0493 |
0,0024 |
5,1 |
3,8 |
3,7291 |
0,0709 |
0,0050 |
3,7590 |
0,0410 |
0,0017 |
5,8 |
4,6 |
4,3738 |
0,2262 |
0,0512 |
4,6606 |
-0,0606 |
0,0037 |
|
|
|
|
0,2011 |
|
|
0,0424 |
Как следует из последней таблицы, приближение в виде степенной функции в данном случае предпочтительнее.
Задание
По заданной таблице значений x и y, полученных экспериментально, построить методом наименьших квадратов две различные эмпирические формулы и сравнить качество полученных приближений.
Вариант 1
x |
2.21 |
3.82 |
4.43 |
5.34 |
5.84 |
6.19 |
6.29 |
7.87 |
8.91 |
9.22 |
y |
57.43 |
58.56 |
60.66 |
68.31 |
70.5 |
71.3 |
79.31 |
90.112 |
91.52 |
92.55 |
Вариант 2
x |
-6.19 |
-4.45 |
-3.81 |
-3.48 |
-2.08 |
-1.28 |
0.12 |
0.84 |
1.81 |
5.44 |
y |
99.17 |
82.52 |
82.16 |
70.24 |
66.48 |
63.23 |
61.02 |
48.35 |
44.56 |
40.24 |
Вариант 3
x |
2.44 |
2.51 |
2.6 |
2.62 |
2.69 |
2.95 |
2.98 |
3.01 |
3.2 |
3.37 |
y |
106.28 |
107.43 |
113.84 |
114.88 |
115.53 |
117.4 |
118.74 |
119.66 |
120.24 |
120.6 |
Вариант 4
x |
3.78 |
3.87 |
4.21 |
4.23 |
4.33 |
2.95 |
4.87 |
5.14 |
5.59 |
5.61 |
y |
65.72 |
60.05 |
59.74 |
58.05 |
56.81 |
55.79 |
50.83 |
47.69 |
45.82 |
44.49 |
Вариант 5
x |
8.74 |
8.77 |
8.81 |
8.90 |
8.98 |
9.11 |
9.14 |
9.22 |
9.31 |
9.35 |
y |
51.67 |
52.76 |
55.65 |
58.86 |
61.09 |
67.68 |
70.44 |
72.19 |
85.02 |
105.2 |
Вариант 6
x |
-1.45 |
-1.82 |
-1.47 |
-0.09 |
0.28 |
0.86 |
1.13 |
2.52 |
3.36 |
3.75 |
y |
23.22 |
28.76 |
35.14 |
39.27 |
40.55 |
52.09 |
55.18 |
59.44 |
62.33 |
65.48 |
Вариант 7
x |
-10.15 |
-10.01 |
-9.96 |
-9.54 |
-9.22 |
-8.88 |
-8.69 |
-8.13 |
-7.85 |
-7.41 |
y |
0.35 |
2.56 |
2.91 |
3.14 |
3.48 |
4.07 |
4.49 |
5.62 |
5.98 |
6.22 |
Вариант 8
x |
2.34 |
2.67 |
2.92 |
3.09 |
3.78 |
4.12 |
4.55 |
4.92 |
5.21 |
5.75 |
y |
-10.12 |
-10.03 |
-9.67 |
-9.34 |
-9.15 |
-8.68 |
-8.43 |
-8.26 |
-7.84 |
-7.11 |
Вариант 9
x |
4.74 |
4.77 |
4.81 |
4.90 |
4.98 |
5.11 |
5.14 |
5.22 |
5.31 |
5.35 |
y |
52.45 |
46.67 |
46.50 |
42.96 |
38.11 |
35.76 |
29.34 |
22.17 |
18.84 |
15.57 |
Вариант 10
x |
5.44 |
5.51 |
5.6 |
5.62 |
5.69 |
5.95 |
5.98 |
6.01 |
6.2 |
6.37 |
y |
-10.28 |
-10.43 |
-11.84 |
-11.88 |
-12.53 |
-12.74 |
-13.74 |
-13.66 |
-14.24 |
-14.6 |
Вариант 11
x |
2.4 |
2.91 |
3.42 |
3.93 |
4.44 |
4.95 |
5.46 |
5.97 |
6.48 |
6.99 |
y |
4.03 |
3.10 |
2.44 |
1.96 |
1.58 |
1.29 |
1.04 |
0.85 |
0.69 |
0.43 |
Вариант 12
x |
1.16 |
1.88 |
2.60 |
3.32 |
4.04 |
4.76 |
5.48 |
6.20 |
6.92 |
7.64 |
y |
0.18 |
0.26 |
0.32 |
0.36 |
0.40 |
0.43 |
0.46 |
0.48 |
0.50 |
0.51 |
Вариант 13
x |
1.00 |
1.71 |
2.42 |
3.13 |
3.84 |
4.55 |
5.26 |
5.97 |
6.68 |
7.39 |
y |
12.49 |
4.76 |
2.55 |
1.60 |
1.11 |
0.82 |
0.63 |
0.50 |
0.41 |
0.36 |
Вариант 14
x |
-0.64 |
-0.36 |
-0.08 |
0.20 |
0.48 |
0.76 |
1.04 |
1.32 |
1.60 |
1.88 |
y |
29.51 |
18.86 |
12.05 |
7.70 |
4.92 |
3.14 |
2.01 |
1.28 |
0.93 |
0.71 |
Вариант 15
x |
-2.45 |
-1.94 |
-1.43 |
-0.92 |
-0.41 |
0.10 |
0.61 |
1.12 |
1.63 |
2.14 |
y |
0.87 |
1.19 |
1.68 |
2.23 |
3.04 |
4.15 |
5.66 |
7.72 |
8.82 |
10.05 |
Вариант 16
x |
1.54 |
1.91 |
2.28 |
2.65 |
3.02 |
3.39 |
3.76 |
4.13 |
4.50 |
4.87 |
y |
-2.52 |
-3.08 |
-3.54 |
-3.93 |
-4.27 |
-4.57 |
-4.84 |
-5.09 |
-5.29 |
-5.44 |
Вариант 17
x |
1.2 |
2.0 |
2.8 |
3.6 |
4.4 |
5.2 |
6.0 |
6.8 |
7.6 |
8.4 |
y |
-10.85 |
-6.15 |
-4.14 |
-3.02 |
-2.30 |
-1.81 |
-1.45 |
-1.17 |
-0.96 |
-0.81 |
Вариант 18
x |
-1.04 |
-0.67 |
-0.30 |
0.07 |
0.44 |
0.81 |
1.18 |
1.55 |
1.92 |
2.29 |
y |
10.80 |
8.08 |
5.97 |
4.44 |
3.31 |
2.46 |
1.83 |
1.36 |
0.78 |
0.25 |
Вариант 19
x |
0.41 |
0.97 |
1.53 |
2.09 |
2.65 |
3.21 |
3.77 |
4.33 |
4.89 |
5.45 |
y |
0.45 |
1.17 |
1.56 |
1.82 |
2.02 |
2.18 |
2.31 |
2.44 |
2.55 |
2.64 |
Вариант 20
x |
0.80 |
1.51 |
2.22 |
2.93 |
3.64 |
4.35 |
5.06 |
5.77 |
6.48 |
7.19 |
y |
9.22 |
6.35 |
5.31 |
4.77 |
4.45 |
4.23 |
4.07 |
3.44 |
3.21 |
3.05 |
Вариант 21
x |
-0.05 |
-0.04 |
-0.88 |
0.32 |
-0.24 |
-1.05 |
0.57 |
0.01 |
0.40 |
0.79 |
y |
11.13 |
3.49 |
8.91 |
14.83 |
1.80 |
13.50 |
3.70 |
-2.40 |
10.00 |
16.04 |
Вариант 22
x |
63.96 |
44.39 |
51.20 |
58.44 |
50.15 |
44.51 |
47.25 |
35.24 |
43.28 |
32.03 |
y |
3.05 |
2.20 |
0.65 |
1.65 |
1.92 |
1.92 |
0.89 |
0.75 |
2.79 |
0.44 |
Вариант 23
x |
58.46 |
36.05 |
31.17 |
16.17 |
11.16 |
69.23 |
58.08 |
43.13 |
73.24 |
42.86 |
y |
0.22 |
-3.05 |
-1.76 |
-1.25 |
-0.45 |
-0.80 |
-0.26 |
-3.07 |
-1.27 |
-3.05 |
Вариант 24
x |
66.58 |
36.05 |
64.63 |
33.19 |
26.70 |
55.31 |
18.70 |
22.95 |
38.24 |
9.18 |
y |
3.44 |
1.72 |
2.06 |
3.07 |
0.99 |
7.65 |
2.92 |
3.53 |
4.10 |
-0.47 |
Вариант 25
x |
79.31 |
57.34 |
60.66 |
92.55 |
90.12 |
71.30 |
70.50 |
91.52 |
68.31 |
58.56 |
y |
5.84 |
3.82 |
6.19 |
9.22 |
7.87 |
6.29 |
4.43 |
8.91 |
5.34 |
2.21 |
Вариант 26
x |
82.16 |
61.02 |
44.56 |
82.52 |
99.17 |
70.24 |
63.23 |
66.48 |
48.35 |
40.24 |
y |
0.12 |
-3.48 |
-4.45 |
-6.19 |
1.81 |
-3.81 |
0.84 |
-2.08 |
-1.28 |
5.44 |
Вариант 27
x |
65.72 |
58.05 |
60.05 |
55.79 |
50.83 |
47.69 |
44.49 |
59.74 |
56.81 |
45.82 |
y |
5.14 |
5.59 |
4.33 |
4.59 |
4.21 |
3.78 |
4.23 |
5.61 |
4.87 |
3.87 |
Вариант 28
x |
55.65 |
67.68 |
105.20 |
85.02 |
52.76 |
58.86 |
72.19 |
61.09 |
70.44 |
51.67 |
y |
9.11 |
9.35 |
8.90 |
9.22 |
8.74 |
8.98 |
8.77 |
9.31 |
8.81 |
9.14 |