§ 1. Общая схема исследования и построения графика функции.
Нахождение области определения функции (области допустимых значения аргумента-ОДЗ).
Сужение (уменьшение) рассматриваемой области определения для четных (нечетных), а также для периодических функций.
Поведение функции на границах области определения - находится с помощью вычисления соответствующих пределов.
Нанесение значений вычисленных пределов на координатную плоскость. Предварительный рисунок графика функций.
Проверка существования дифференцируемых и недифференцируемых локальных экстремумов. (Нахождение критических точек – точек обращения в нуль производной; точек разрыва производной, обращения ее в бесконечность).
Уточнение предполагаемого графика функции по найденным локальным экстремумам и точкам разрыва производной. Нанесение на график функции характерных точек функции и точек пересечения с осями координат.
Дальнейшее уточнение графика функции, если это требуется.
( Нахождение наклонных асимптот, точек перегиба и др.).
Окончательное построение графика функции с продолжением его на всю область определения (если было сужение области, связанное с четностью, периодичностью функции).
§ 2. Примеры построения графиков функций
Пр.1
Построим
график функции
.
ОДЗ:
.
С
учетом нечетности функции
произведем сужение области определения,
отбрасывая из рассмотрения область
отрицательных значений аргумента:
ОДЗ:
.
Выясним поведение функции на границах ОДЗ:
;
.
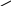
Нанесем на координатную плоскость результаты вычисления пределов (Рис. 1):
y
y
Р
ис.1 
Рис.
2
0
1
x
0 1 x
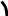
Теперь можно нарисовать предположительный вид графика функции (Рис. 2).
Убедимся, в справедливости нашего предположения. Проверим, что на графике отсутствуют локальные экстремумы.
Найдем первую производную функции, попытаемся приравнять ее нулю:
.
Поскольку в числителе имеем отрицательное число, производная в нуль не обращается. Следовательно, критических точек на графике функции нет, как нет и дифференцируемых экстремумом.
Найдем,
в каких точках производная не существует
или обращается в бесконечность.
Приравнивая знаменатель производной
нулю, получаем значение такой точки:
.
Однако из Рис.
2 мы уже
знали, что при
производная обращается в бесконечность
(слева от
это
,
справа
).
Таким образом, на Рис.
2 график
изображен правильно.
Сделаем
одно уточнение. Найдем под каким углом
пересекает начало координат график
функции. Для этого подставим абсциссу
начала координат
в найденную производную:
.
Таким
образом пересечение графика функции
начала координат осуществляется под
углом
,
примерно так, как мы и нарисовали.
С учетом нечетности функции, продолжим график функции на всю числовую ось, и окончательно получим искомый график (Рис. 3).
y Рис.
4
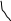
-1 0 1 x
Пр.2
Построим
график функции.
.
ОДЗ:
.
Исследуем поведение функции на границах области определения:
о
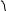
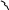
о о
;
;
;
;
;
;
о
.
о о
Нанесем результаты вычисления пределов на координатную плоскость (Рис. 5):
y
Рис. 5
-1
0 1 2 3
x
Предположительный график функции теперь может быть изображен на Рис.6:
y
Рис.
6
-1
0 3 x
2
Теперь
остается убедиться в существовании
одного экстремума (одного максимума с
координатами (
))
изображенного на Рис.6.
Найдем
координаты
.
Для этого вычислим производную функции:
Приравнивая производную нулю, находим что единственным
действительным
корнем числителя является значение
,
где 
.
Соответствующее
значения функции
.
Таким образом, предположительный график функции, изображенный на Рис. 6 , соответствует действительности. Точка пересечения графика с осью абсцисс: . ( В этой точке функция, обращается в нуль.)
Пр.3
Построим
график функции
.
ОДЗ:
.
Учитывая,
что функция четная (функция не «чувствует»
изменения знака
,
т. е.
,
произведем сужение области определения
функции, ограничиваясь рассмотрением
только положительных
:
ОДЗ:
.
Выясним поведение функции на границах области определения:
.
Добавление (-0) показывает, что предельное значение 1 достигается функцией, которая при конечных принимает значения, меньшие единицы.
Наносим значения вычисленных пределов на координатную плоскость (Рис. 7):
y
y
1 1
Р
ис.
7 Рис. 8
X x
Предполагаемый график функции изображен на Рис. 8. График функции при всех значениях располагается ниже прямой линии . Сама прямая является горизонтальной асимптотой. График будет иметь такой вид, если функция во внутренних точках ОДЗ не имеет экстремумов. Проверим это. Найдем производную функции:
.
Ввиду того, что числитель дроби не обращается в ноль, производная функции не равна нулю, следовательно на графике отсутствуют дифференцируемые локальные экстремумы. Таким образом, предполагаемый график функции (Рис. 8) действительно является графиком функции.
Для уточнения графика найдем точки разрыва производной. Таким точкам соответствует случай обращения производной в бесконечность. Для этого знаменатель у производной должен обратиться в ноль. Единственная возможность для этого - обращение в ноль . Таким образом, при производная функции обращается в бесконечность и график функции пересекает начало координат вертикально. Учитывая последнее обстоятельство, и продолжая график функции на всю область определения, с учетом четности функции окончательно получаем искомый график (Рис. 9).
y
1
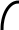
x
Рис. 9
На
графике имеется горизонтальная асимптота
при
Построение графиков функций. Типовые задания.
В этом разделе будет предложено десять типовых задач на построение графиков функций, основные типы которых были рассмотрены в предыдущем параграфе в виде десяти разобранных примеров построения графиков. Каждая задача представлена в 10 вариантах. Все варианты равноценны, имеют один уровень сложности и могут быть решены одинаковыми методами.
Общее задание: Используя алгоритм исследования и построения графика функции § 1, руководствуясь примерами построения графиков функций § 2, сделать рисунки следующих графиков функций.
Задача 1.
.
.
.
.
.
.
.
.
.
.
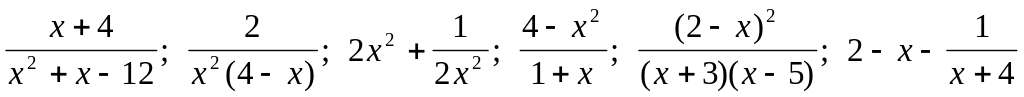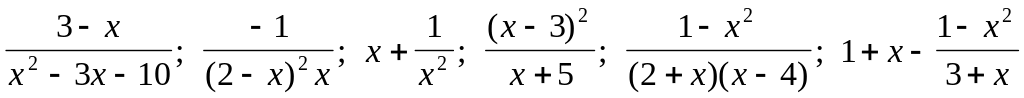Задача 2.
.
.
.
.
.
.
.
.
.
Задача 3.
.
.
.
.
.
.
.
.
.
.
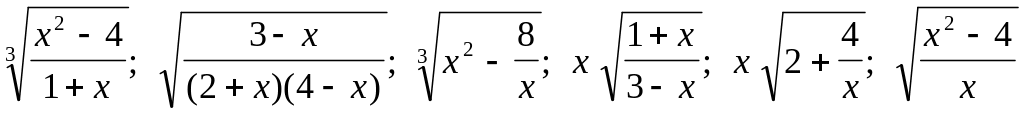ИНТЕГРИРОВАНИЕ
Задача 1. Вычислить неопределенный интеграл
Пример решения задачи 1. Вычислить неопределенный интеграл
.
Решение: Искомый интеграл представляет собой сумму интегралов:
,
.
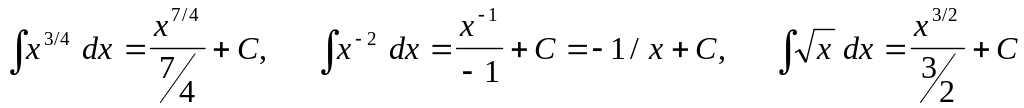При интегрировании были использованы формулы:
.
Задача 2. Вычислить неопределенный интеграл
2.1
2.2
2.3
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
Пример решения задачи 2. Вычислить неопределенный интеграл
.
Искомый интеграл равен сумме следующих интегралов:
,
,
,
,
,
Здесь помимо правила интегрирования сложной функции
были использованы табличные интегралы
,
а также свойства дифференциала:
и интеграла
,
где
.
Задача 3. Вычислить неопределенный интеграл
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10