
- •Кафедра автоматизированных систем управления
- •1.2. Упражнения
- •2. Практическое занятие №2. Решение слау. Вычисление определителей и обратных матриц. Вычисление норм векторов и матриц, чисел обусловленности матриц
- •2.1. Краткие теоретические сведения
- •2.1.1. Методы решения слау
- •2.1.2. Вычисление определителей и обратных матриц
- •2.1.3. Вычисление норм векторов и матриц, чисел обусловленности матриц
- •2.2. Упражнения
- •3. Практическое занятие №3. Определение собственных чисел и собственных векторов матрицы
- •3.1. Краткие теоретические сведения
- •3.2. Упражнения
- •4. Практическое занятие №4. Численное дифференцирование
- •4.1. Краткие теоретические сведения
- •4.2. Упражнения
- •5. Практическое занятие №5. Решение обыкновенных дифференциальных уравнений
- •5.1. Краткие теоретические сведения
- •5.2. Упражнения
- •6. Индивидуальное домашнее задание
- •6.1. Темы и порядок выбора задания
- •6.2. Содержание отчета по индивидуальному заданию
- •7. Литература
- •Численные методы
3.2. Упражнения
1. Дана матрица
 .
.
А) Степенным методом найти несколько последовательных приближений к доминирующему собственному числу матрицы А и к соответствующему собственному вектору.
Б) Методом обратных итераций найти младшую собственную пару {3, x3}.
2. Найти приближения к собственным числам матрицы А степенным методом.
 .
.
3. Найти приближение к доминирующему собственному числу матрицы А и к соответствующему собственному вектору методом скалярных произведений.
 .
.
4. Методом вращений Якоби решить задачу нахождения всех собственных пар матрицы А, если
1)
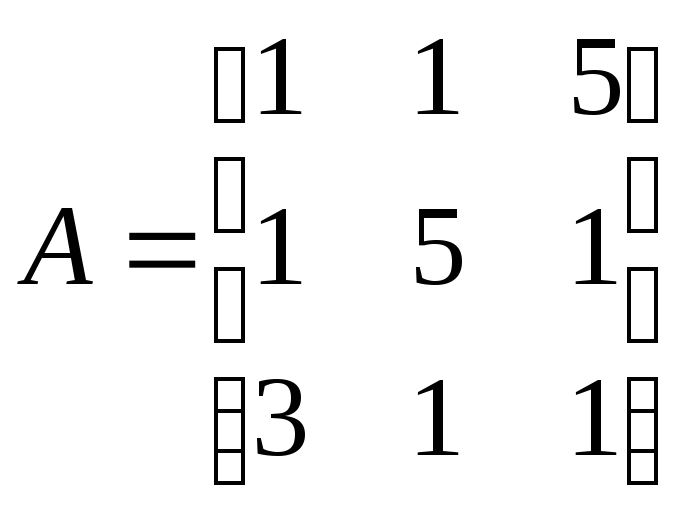 ,
2)
,
2)
![]() .
.
5. Для n×n матрицы сделать приблизительный подсчет количества арифметических операций, приходящихся на:
а) один шаг степенного метода;
б) один шаг метода обратных итераций;
в) один полный цикл метода вращений Якоби.
4. Практическое занятие №4. Численное дифференцирование
4.1. Краткие теоретические сведения
Источником формул численного дифференцирования является полиномиальная интерполяция. Зная значения yi = f(xi) заданной функции f(x) в точках xi = x0+ih (i = 0, 1, …, n) при некотором h > 0, можно найти конечные разности kyi (=k-1yi+1 – k-1yi) и записать для нее, например, первый интерполяционный многочлен Ньютона Pn(x) (см. далее). Дифференцируя приближенное равенство f(x) Pn(x), можно строить формулы приближенного дифференцирования различной точности [1]. Пусть q = (x – x0)/h. Приближенное представление f(x) по первой формуле Ньютона имеет вид:
![]() .
Тогда конечноразностная формула
численного дифференцирования имеет
вид:
.
Тогда конечноразностная формула
численного дифференцирования имеет
вид:
![]()
![]() ,
,
![]() .
(8)
.
(8)
Для приближенного вычисления производной функции в заданной точке x* из некоторой окрестности x0 следует найти соответствующее значение q* и подставить в формулу (8).
В частных случаях:
на основе линейной интерполяции ![]() ,
для
x(x0-,
x1+),
на основе квадратичной интерполяции
,
для
x(x0-,
x1+),
на основе квадратичной интерполяции ![]() для x(x0-,
x2+)
и т.д. Т.к. точкам x0,
x1,
x2,
... соответствуют значения q
= 0, 1, 2, …, при n
= 1, для линейной интерполяции получаются
следующие формулы первого порядка
точности:
для x(x0-,
x2+)
и т.д. Т.к. точкам x0,
x1,
x2,
... соответствуют значения q
= 0, 1, 2, …, при n
= 1, для линейной интерполяции получаются
следующие формулы первого порядка
точности:
![]() .
.
Использование таких аппроксимаций дает ошибку O(h). Для формул второго порядка точности имеется ошибка O(h2).
Повторное дифференцирование приближенного равенства (8), т.е. взятие производной по x от правой части (8) с учетом dq/dx = 1/h, приводит к конечноразностной формуле вычисления второй производной
![]() , (9)
, (9)
из которой аналогично следует приближенная формула третьей производной
![]() и т.д.
и т.д.
Для построения простой аппроксимации второй производной из разложения функции f(x) в окрестности точки xi
![]() при x
= xi+1
и x
= xi-1
можно записать:
при x
= xi+1
и x
= xi-1
можно записать:
![]() ,
,
![]() ,
,
откуда после
почленного сложения получается формула
симметричной аппроксимации ![]() c
остаточным членом:
c
остаточным членом:
![]() .
(10)
.
(10)
По формуле Тейлора для второй производной
![]() .
После подстановки сюда правой части
(10) вместо
.
После подстановки сюда правой части
(10) вместо ![]() получается равенство:
получается равенство:
![]() .
Из него при x
= xi+1
и x
= xi-1
следуют формулы несимметричной
аппроксимации второй производной с
остаточными членами:
.
Из него при x
= xi+1
и x
= xi-1
следуют формулы несимметричной
аппроксимации второй производной с
остаточными членами:
![]() и
и
![]() .
.
4.2. Упражнения
1. Вывести частные формулы аппроксимации второй производной в равноотстоящих узлах, основываясь на квадратичной интерполяции.
2. Вывести частные формулы аппроксимации второй производной в равноотстоящих узлах, основываясь на кубической интерполяции.
3. Записать
симметричную формулу четвертого порядка
точности для аппроксимации ![]() и вывести ее остаточный член, используя
формулу Тейлора.
и вывести ее остаточный член, используя
формулу Тейлора.
4. Вывести общую формулу численного дифференцирования, используя формулу Ньютона для неравных промежутков:
![]()
где
![]() – разделенная разность первого порядка,
– разделенная разность первого порядка,
![]() –разделенная
разность второго порядка и т.д.
–разделенная
разность второго порядка и т.д.
5. Вывести частные формулы аппроксимации второй производной в неравноотстоящих узлах, основываясь на квадратичной интерполяции.
