Практическое занятие №32

Наименование занятия: Действия над комплексными числами в алгебраической и геометрической формах

Цель занятия: Научиться выполнять действия над комплексными числами.

Подготовка к занятию: Повторить теоретический материал по теме «Комплексные числа».

Литература:

1. Дадаян И.И. «Математика»

Задание на занятие:

1. Решить квадратные уравнения:

1. x² + 2x + 5 = 0;

2. x² – 6x + 18 = 0;

3. x² - 4x + 5 =0.

2. Выполнить действия:

1. i + i³³;

2. i¹⁷ + i(1- i);

3. (1 + i)³;

4. ;

5. .

3. Изобразить на плоскости комплексные числа, их сумму и разность:

   1. Z₁ = -2 + i; Z₂ = 2 – 3i;

   2. Z₁ = -3 - i; Z₂ = 1 – 4i.

Порядок проведения занятия:

1. Получить допуск к работе

2. Выполнить задания

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Что называется мнимой единицей? Как вычисляются степени мнимой единицы?

2. Какое число называется комплексным?

3. Как геометрически изображаются комплексные числа?

4. Какие комплексные числа называются сопряженными?

5. Как выполняются сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме?

6. Какие корни и сколько корней имеет квадратное уравнение с отрицательным дискриминантом?

Составила преподаватель: Лобачева М.Е.

Практическое занятие №33

Наименование занятия: Действия над комплексными числами в тригонометрической и показательной формах

Цель занятия: Научиться выполнять действия над комплексными числами.

Подготовка к занятию: Повторить теоретический материал по теме «Комплексные числа».

Литература:

1. Дадаян И.И. «Математика»

Задание на занятие:

1. Представить комплексные числа в тригонометрической и показательной формах:

   1. Z = -1 + i;

   2. Z = -2.

2. Выполнить действия и записать результат в тригонометрической форме:

   1. ;

   2. .

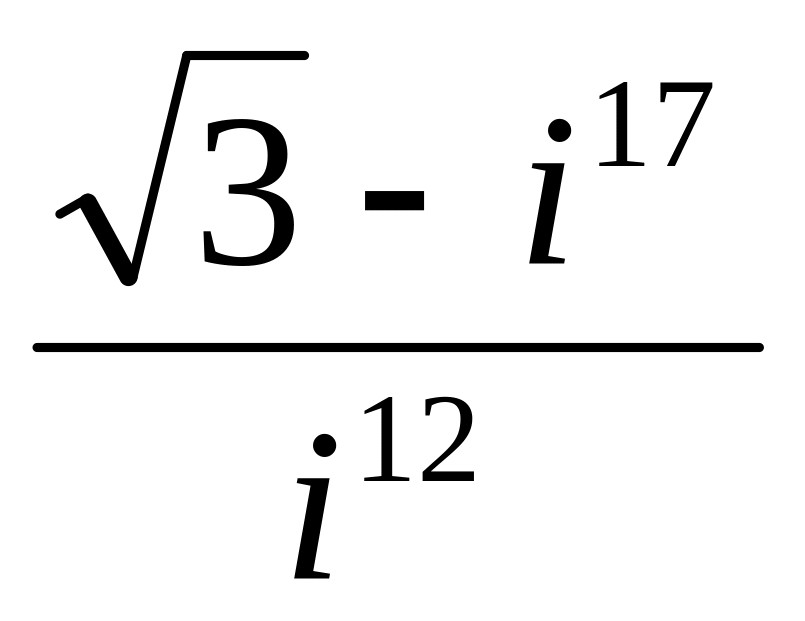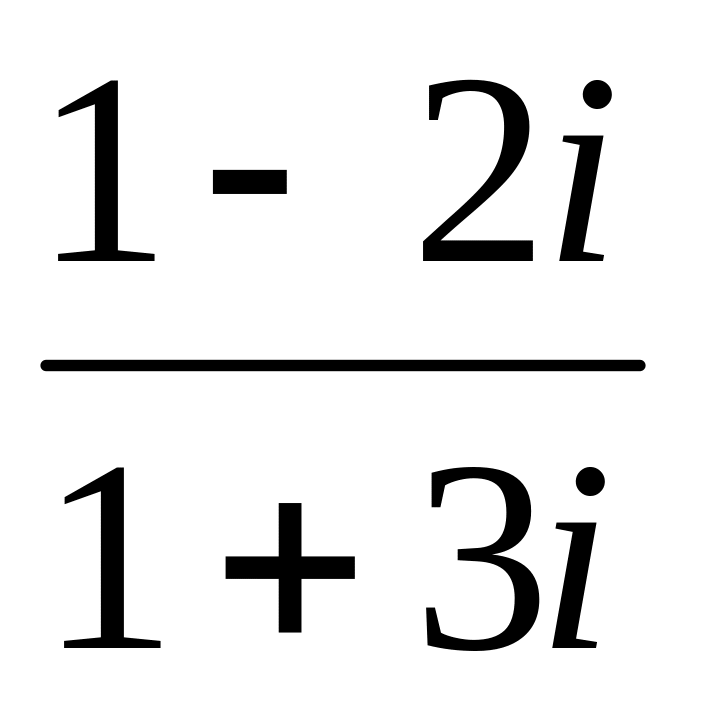3. Выполнить действия:

   1. ;

   2. ;

   3. ;

   4. 

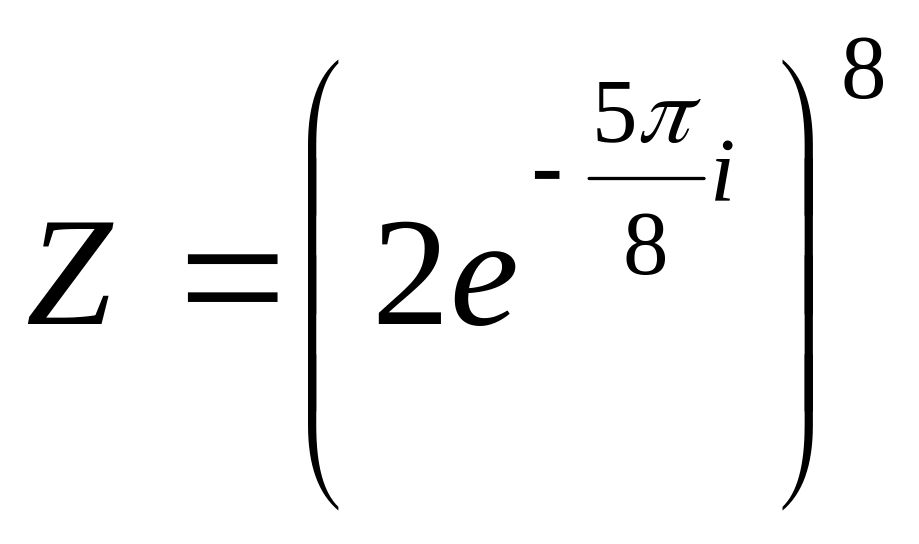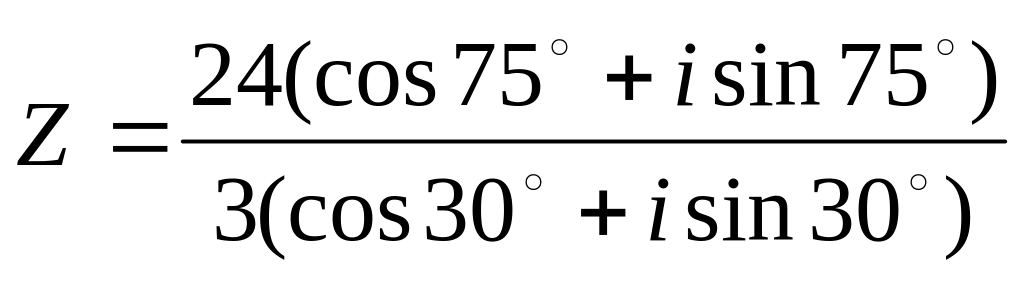4. Выполнить действия и записать результат в показательной форме:

1. ;

2. 

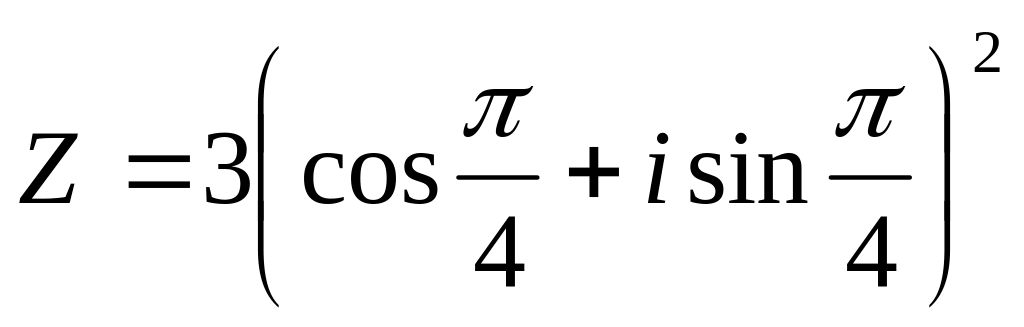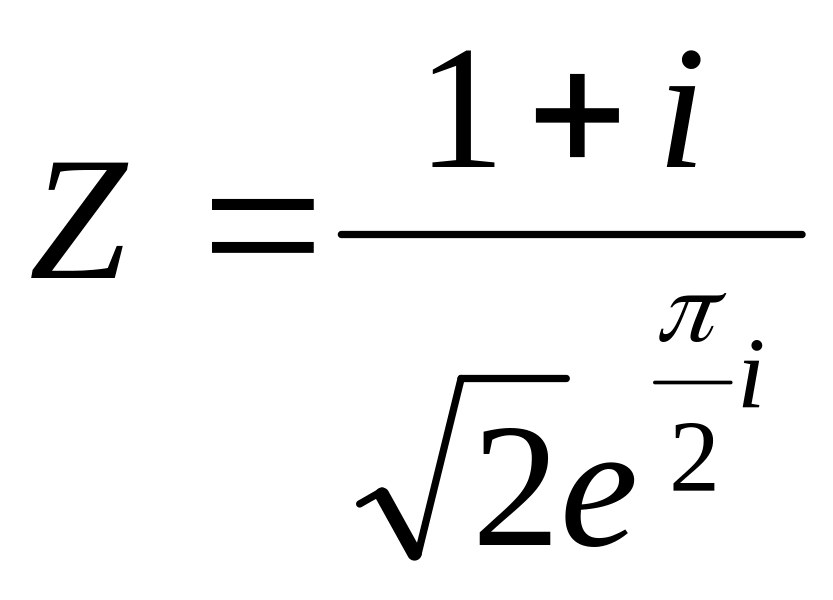
Порядок проведения занятия:

1. Получить допуск к работе

2. Выполнить задания

3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;

2. Выполненное задание;

3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Что называется модулем и аргументом комплексного числа? Как они вычисляются?

2. Как записывается комплексное число в тригонометрической, показательной формах?

3. Как найти произведение и частное комплексных чисел, записанных в тригонометрической, показательной формах?

4. Как возвести в степень число, записанное в тригонометрической, показательной формах?

Практическое занятие №34

Наименование занятия: Решение комбинаторных задач

Цель занятия: Научиться решать комбинаторные задачи

Подготовка к занятию: Повторить теоретический материал по теме «Элементы комбинаторики»

Литература: