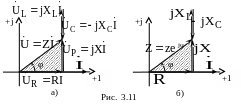- •© Оформление. Фгбоу во
- •«Воронежский государственный
- •Технический университет», 2015
- •Введение
- •Указания по технике безопасности
- •Требования к подготовке и оформлению лабораторных работ
- •Источники электрической энергии
- •Приемники электрической энергии
- •Закон Ома
- •Законы Кирхгофа
- •Режимы работы источников электрической энергии
- •Эквивалентные преобразования пассивной части электрической цепи
- •Расчет электрических цепей путем непосредственного применения законов Кирхгофа
- •Потенциальная диаграмма
- •Баланс мощностей
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •Метод эквивалентного генератора
- •Передача энергии от активного двухполюсника к пассивному
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •Контрольные вопросы
- •Среднее и действующее значения синусоидального тока
- •Представление синусоидальных токов и напряжений векторами. Комплексные токи и напряжения
- •Действия с комплексными числами
- •Линейные элементы r, l, c в цепи синусоидального тока
- •Последовательное соединение идеальных элементов r, l, c
- •Векторные диаграммы для цепи с последовательным соединением идеальных элементов r, l, c. Треугольник напряжений. Треугольник сопротивлений
- •Активная, реактивная и полная мощности. Комплексная мощность
- •Параллельное соединение идеальных элементов r, l, c
- •Векторные диаграммы для цепи с параллельным соединением идеальных элементов r, l, c
- •Схемы замещения реальной индуктивной катушки и конденсатора
- •Параллельное соединение реальных индуктивной катушки и конденсатора
- •Определение параметров пассивного двухполюсника опытным путем
- •Резонансные режимы в цепях синусоидального тока
- •Коэффициент мощности
- •Описание лабораторной установки
- •Построение векторных диаграмм по опытным данным
- •Контрольные вопросы
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Вращающееся магнитное поле
- •Схемы соединения фаз трехфазной нагрузки
- •Соединение фаз трехфазной нагрузки «звездой»
- •Расчет мощности трехфазного приемника
- •Расчет токов и напряжений для различных режимов работы трехфазных цепей при соединении фаз нагрузки «звездой»
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •Контрольные вопросы
- •Режимы работы трехфазной нагрузки, соединенной по схеме «треугольник»
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •Построение векторных диаграмм по опытным данным
- •Контрольные вопросы
- •Действующее и среднее значения несинусоидальных электрических величин
- •Активная, реактивная и полная мощности
- •Коэффициенты, характеризующие форму несинусоидальных кривых
- •Расчет электрических цепей при несинусоидальных токах и напряжениях
- •Алгоритм расчета токов и напряжений в линейных цепях при воздействии несинусоидальной эдс
- •Измерение несинусоидальных периодических токов и напряжений
- •Примеры расчета токов и напряжений в линейных цепях при воздействии несинусоидальной эдс
- •Резонансные явления в цепи несинусоидального тока
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •Лабораторная работа № 8 четырехполюсник
- •Теоретические сведения
- •Уравнения четырехполюсника
- •Определение коэффициентов а- и в- форм записи уравнений четырехполюсника
- •Вторичные параметры четырехполюсника
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •Построение линейных векторных диаграмм четырехполюсников
- •Переходные процессы в линейных электрических цепях
- •Теоретические сведения
- •Законы коммутации
- •Классический метод расчета переходных процессов
- •Алгоритм расчета переходных процессов классическим методом
- •Переходный процесс в цепи с последовательно соединенными резистором и катушкой индуктивности
- •Переходный процесс в цепи с последовательно соединенными резистором и конденсатором
- •Переходные процессы в неразветвленной цепи r, l, с
- •Задание на подготовительную работу
- •Программа работы
- •Феррорезонанс напряжения
- •Феррорезонанс токов
- •Задание на подготовительную работу
- •Программа работы
- •Контрольные вопросы
- •Экспериментальное получение вах
- •Статическое и динамическое сопротивления нэ
- •Графический метод расчета нелинейных цепей постоянного тока
- •Стабилизатор напряжения
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •Контрольные вопросы
- •Выпрямительный диод с емкостным фильтром
- •Управляемый вентиль с активно-реактивной нагрузкой
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •5. Изучить порядок работы с двухлучевым осциллографом. Программа работы
- •Контрольные вопросы
- •Заключение
- •Пример оформления титульного листа рабочей тетради
- •Рабочая тетрадь
- •13.04.02 «Электроэнергетика и электротехника» очной формы обучения
- •Библиографический список
- •Оглавление
- •3 94026 Воронеж, Московский просп., 14
Последовательное соединение идеальных элементов r, l, c
В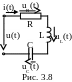 цепи, состоящей из последовательно
соединенных элементов R,
L, C (рис.
3.8) с известным синусоидальным током
i(t)=Imsin(ωt
+ ψi) уравнение
для напряжения на ее зажимах запишем
по второму закону Кирхгофа:
цепи, состоящей из последовательно
соединенных элементов R,
L, C (рис.
3.8) с известным синусоидальным током
i(t)=Imsin(ωt
+ ψi) уравнение
для напряжения на ее зажимах запишем
по второму закону Кирхгофа:
![]()
Сумме
синусоидальных напряжений соответствует
сумма изображающих их комплексных
величин. Для действующих комплексных
значений:
![]() где комплексные напряжения на элементах
цепи определяют согласно закону Ома:
где комплексные напряжения на элементах
цепи определяют согласно закону Ома:
![]()
Тогда
![]() .
.
Закон
Ома в комплексной форме записи:
![]() ,
,
где Z
– комплексное сопротивление участка
цепи, которое определяют как сумму
комплексных сопротивлений каждого из
последовательно соединенных элементов:
![]()
или в показательной форме записи:
![]()
где
модуль комплексного сопротивления
![]() называют полным
сопротивленем; аргумент комплексного
сопротивления - угол
сдвига фаз между входным
напряжением и током, определяется
соотношением реактивных и активных
сопротивлений рассматриваемого участка:
называют полным
сопротивленем; аргумент комплексного
сопротивления - угол
сдвига фаз между входным
напряжением и током, определяется
соотношением реактивных и активных
сопротивлений рассматриваемого участка:
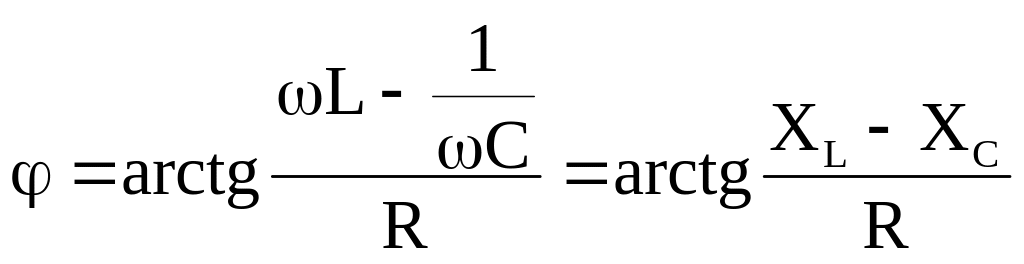 .
.
При
![]() или XL>XC
угол φ>0 и ток отстает по фазе от
напряжения;
или XL>XC
угол φ>0 и ток отстает по фазе от
напряжения;
при
![]() или XL<XC
угол φ <0 и ток опережает напряжение
по фазе;
или XL<XC
угол φ <0 и ток опережает напряжение
по фазе;
при
![]() или XL=XC
угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление. Такой режим работы цепи
называют режимом
резонанса напряжений.
или XL=XC
угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление. Такой режим работы цепи
называют режимом
резонанса напряжений.
Согласно закону Ома комплексное действующее значе- ние напряжения:
![]()
где
![]() - действующее значение приложенного к
цепи напряжения;
- действующее значение приложенного к
цепи напряжения;
![]() - начальная фаза напряжения;
- начальная фаза напряжения;
![]() -
угол сдвига фаз между напряжением на
зажимах цепи и током.
-
угол сдвига фаз между напряжением на
зажимах цепи и током.
Мгновенное
значение напряжения на входе цепи имеет
вид:
![]()
Векторные диаграммы для цепи с последовательным соединением идеальных элементов r, l, c. Треугольник напряжений. Треугольник сопротивлений
В цепи
с последовательным соединением элементов
R, L,
C ток во
всех участках один и тот же, а напряжения
связаны между собой вторым законом
Кирхгофа. В комплексной или векторной
форме запишем:
![]()
П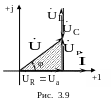 остроим
векторную диа- грамму тока и напряжений
на участках цепи с элементами R,
L, C
(рис. 3. 9). Примем начальную фазу тока
равной нулю (ψi=0).
Напряжение
остроим
векторную диа- грамму тока и напряжений
на участках цепи с элементами R,
L, C
(рис. 3. 9). Примем начальную фазу тока
равной нулю (ψi=0).
Напряжение
![]() на
резистивном элементе совпадает по фазе
c током, напряжение на
индуктивном элементе
на
резистивном элементе совпадает по фазе
c током, напряжение на
индуктивном элементе
![]() опережает
ток на 90°, напряжение на емкостном
элементе
опережает
ток на 90°, напряжение на емкостном
элементе
![]() отстает от тока по фазе на 90°. Напряжение
на входе цепи получим как векторную
сумму напряжений элементов согласно
второму закону Кирхгофа.
отстает от тока по фазе на 90°. Напряжение
на входе цепи получим как векторную
сумму напряжений элементов согласно
второму закону Кирхгофа.
Заштрихованный треугольник, показанный на векторной диаграмме (рис. 3.9), принято называть треугольником напряжений.
Проекцию вектора
напряжения на направление вектора тока
называют активной составляющей
напряжения и обозначают
![]() .
Проекцию вектора напряжения на
направление, перпендикулярное вектору
тока, называют реактивной
составляющей напряжения и обозначают
.
Проекцию вектора напряжения на
направление, перпендикулярное вектору
тока, называют реактивной
составляющей напряжения и обозначают
![]() .
.
На векторной диаграмме рис. 3.9 видно:
![]()
![]()
![]()
В соответствии с тремя возможными вариантами соотношения между сопротивлениями реактивных элементов (XL>XC, XL = XC , XL<XC) и соответствующими им напряжениями (UL>UC, UL = UC , UL<UC) можно построить три векторные диаграммы для каждого из случаев (рис. 3.10, а, б, в). Угол φ положителен при отстающем токе (рис. 3.10, а) и отрицателен при опережающем токе (рис. 3.10, в).
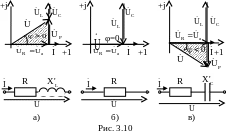
При неизменной частоте источника питания цепь рис. 3.8 можно представить одной из эквивалентных схем, представленных на рис. 3.10: а - при XL>XC как последовательное соединение активного и индуктивного сопротивлений (R и XL´=XL-XC); б - при XL=XC как активное сопротивление R (резонанс напряжений); в - при XL<XC как последовательное соединение активного и емкостного сопротивлений (R и XС´=XL-XC).
Необходимо заметить, что напряжения на L и С - элементах находятся в противофазе, вследствие чего в цепи переменного тока с последовательным соединением элементов могут создаваться условия, невозможные для цепей постоянного тока - когда напряжения на отдельных участках цепи значительно превышают напряжение на входе.
Рассмотрим
треугольник напряжений, в котором каждое
из напряжений записано согласно закону
Ома в комплексной форме (рис. 3.11, а). При
делении каждой стороны этого треугольника
напряжений на комплексную величину
тока получим треугольник, подобный
исходному (рис. 3.11, б). Этот треугольник
называют треугольником сопротивлений.
Его можно получить, построив на
комплексной плоскости диаграмму,
соответствующую выражению комплексного
сопротивления цепи состоящей из
последовательного соединения элементов
R, L,
C:
![]()