3. Решение

Формирование полезного сигнала

>> Ts=0.005;

>> t=0:Ts:20;

>> A0=0.8; T0=0.5;

>> Yp=A0*sin(2*pi*t/T0);

>> plot(t,Yp),grid; title('P-signal'); xlabel('t, c'); ylabel('Yp')

Рисунок 1. Полезный сигнал.

Добавление к исходному сигналу помех и шумов

>> T1=2; A1=7.5; eps=pi/4;

>> Ash=5;

>> x=A0*sin(2*pi*t/T0)+A1*sin(2*pi*t/T1+eps)+Ash*randn(1,length(t));

>> plot(t,x), grid; title('input'); xlabel('t, c'); ylabel('x(t)')

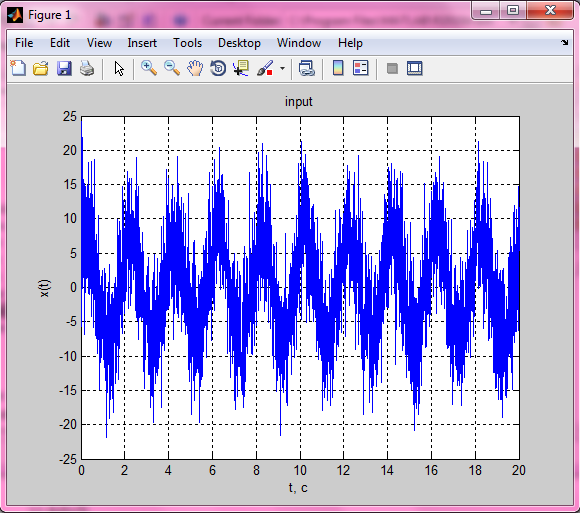
Рисунок 2. Полезный сигнал с шумом и помехами.

Формирование фильтра:

>> Tf=2;dz=0.01;

>> om0=2*pi/Tf;A=1;oms=om0*Ts;

>> a(1)=1+2*dz*oms+oms^2;

>> a(2)= -2*(1+dz*oms);

>> a(3)=1;

>> b(1)=A*Ts*Ts*(2*dz*om0^2);

Процедура двойной фильтрации:

>> y=filtfilt(b,a,x);

>>plot(t,y,t,Yp),grid; title(' procedure filtfilt (Tf=2,dz=0.01)'); xlabel('t, c'); ylabel('Y(t)')

Рисунок 3. Сигнал, пропущенный через двойной фильтр.

Формирование случайного процесса:

>> Ts=0.005;

>> t=0:Ts:20;

>> x1=randn(1,length(t));

>> plot(t,x1),grid;title('Gaus(T=0.005c)');xlabel('t, c');ylabel('X1(t)')

Рисунок 4. Сформированный белый гауссовый шум.

Формирующий фильтр второго порядка с частотой собственных колебаний ω₀ = 2π рад\с =1 Гц и относительным коэффициентом колебаний затухания ξ=0.01

>> om0=2*pi;dz=0.01;A=1;oms=om0*Ts;

>> a(1)=1+2*dz*oms+oms^2;

>> a(2)=-2*(1+dz*oms);

>> a(3)=1;

>> b(1)=A*2*dz*oms^2;

Пропустим образованный процесс через созданный формирующий фильтр:

>> y1=filter(b,a,x1);

>>plot(t,y1),grid; title('procedure filtr (T0=1;dz=0.01;Ts=0.005)'); xlabel('t, c'); ylabel('Y1(t)')

Рисунок 5. Случайный колебательный процесс с преобладающей частотой 3 Гц.

Спектральный и статистический анализ

Входной сигнал представим в виде вектора, элементы которого равны значениям функции, являющейся суммой трех синусоид

>> t=0:0.001:2;

>> x=sin(2*pi*3*t)+sin(2*pi*3*t)+sin(2*pi*4*t);

>> plot(t,x),grid; title('input'); xlabel('t, c'); ylabel('X(t)')

Рисунок 6. Графики входного процесса, состоящего их суммы синусоид 3 Гц, 3 Гц и 4 Гц.

>> y=fft(x);

>> a=abs(y);

>> plot(a);grid; title('fourier'); xlabel('number'); ylabel('absF(X(t))')

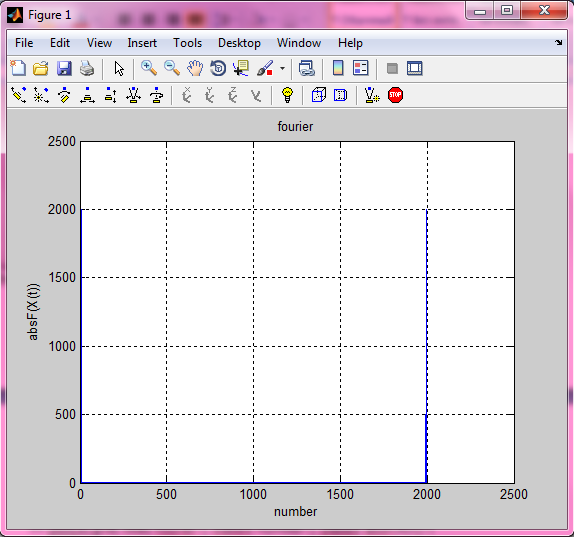
Рисунок 7. Фурье-изображение входного сигнала.

Осуществим обратное преобразование:

>> z=ifft(y);

>> plot(t,z), grid; title('inverse'); xlabel('t, c'); ylabel('Z(t))')

Рисунок 8. Обратное преобразование Фурье для входного сигнала.

Переходим от индексов к временной и частотной области:

>> f=0:0.5:1000

>> plot(f,a);grid; title('F(x)'); xlabel('friquency, Hz'); ylabel('abs(F(X))')

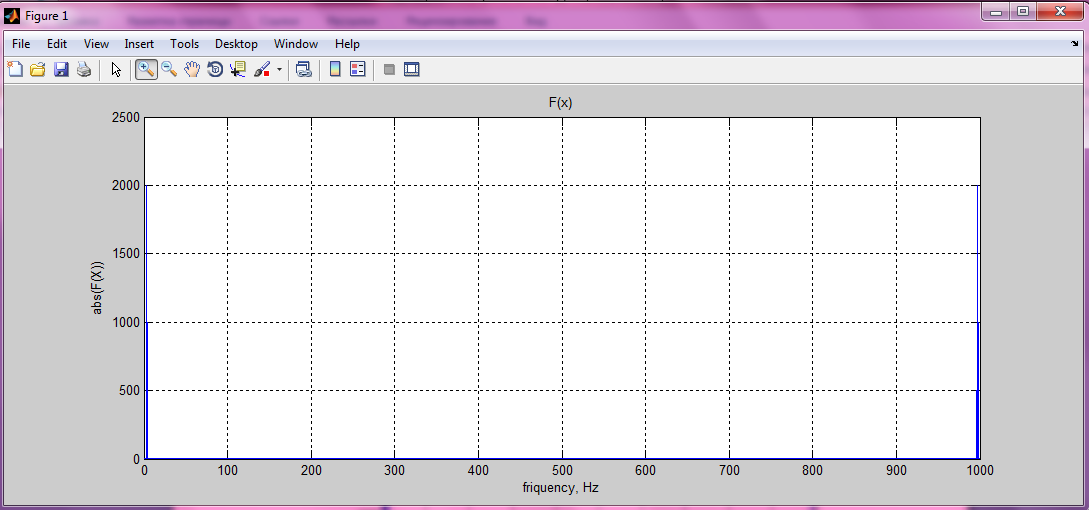
Рисунок 9. График преобразования Фурье с аргументом – частотой.

Установления истинного спектра входного сигнала:

>> f1=-500:0.5:500;

>> v=fftshift(y);

>> a=abs(v);

>> plot(f1(970:1030),a(970:1030));grid; title('F/N'); xlabel('friquency, Hz'); ylabel('abs(F(X))/N')

Рисунок 10. Частотный спектр входного сигнала.

Определим амплитуду гармоник:

>> N=length(y);

>> a=2*abs(v)/N;

>> plot(f1(970:1030),a(970:1030));grid; title('F/N'); xlabel('friquency, Hz'); ylabel('abs(F(X))/N')

Рисунок 11. Частотный спектр входного сигала с амплитудой гармоник в качестве значения ординат

4. Выводы

Цифровая обработка сигналов позволяет не только качественно менять их свойства, но и часто бывает единственным способом выделить полезную информацию из сигнала.

- Путем подбора параметров дискретный фильтр второго порядка позволил снизить шум, введенный в измеряемый сигнал, так что на выходе фильтра сигнал представляет собой полезную гармонику с минимальными изменениями.

- Тот же фильтр позволил сформировать из случайного сигнала (белый шум) необходимый случайный колебательный процесс с преобладающей частотой 3 Гц.

- Путем преобразования Фурье из полученного спектра сигнала хорошо видны линии гармоник, соответствующие частотам 3, 3 и 4 Гц. Также видна амплитуда этих гармоник, которая в точности соответствует заданным значениям.