Задание на работу
Создать модель системы слежения, представленной на рисунке:
На рисунке:
;
;
.
Провести исследование системы, при этом:
- оценить временные отклики системы;
- определить реакцию системы на гармонические воздействия;
- определить полюса и нули системы.
Представить соответствующие графики.
Критерием при исследовании должны служить устойчивость системы и показатели качества.
В случае неудовлетворительного качества системы при исходных параметрах (см. ниже таблицу вариантов) выбрать требуемые параметры корректирующего фильтра W1(s): T1, T2, Kпр.
Исходные параметры заданной системы для каждого варианта заданы в таблице:
|
№ варианта |
T1, c |
T2, c |
T3, c |
T4, c |
Kпр |
Kос |
|
19 |
0.40 |
0.045 |
0.050 |
0.0045 |
8.0 |
1.5 |
Решение
1. Создаем модель системы слежения, с параметрами, соответствующими заданному варианту.
Заносим исходные параметры системы:
k11=tf(8,1)
Transfer function:
8
>> w11=tf([0.4 1],[0.045 1])
Transfer function:
0.4 s + 1
-----------
0.045 s + 1
>> w112=w11*k11
Transfer function:
3.2 s + 8
-----------
0.045 s + 1
>> w12=tf([0.05 1],[0.0045 1 0])
Transfer function:
0.05 s + 1
--------------
0.0045 s^2 + s
>> w13=tf(1, [1 0])
Transfer function:
1
-
s
>> w4=w112*w12*w13
Transfer function:
0.16 s^2 + 3.6 s + 8
--------------------------------
0.0002025 s^4 + 0.0495 s^3 + s^2
>> k12=tf(1.5,1)
Transfer function:
1.5
>> sys1=feedback(w4,k12)
Transfer function:
0.16 s^2 + 3.6 s + 8
--------------------------------------------------
0.0002025 s^4 + 0.0495 s^3 + 1.24 s^2 + 5.4 s + 12
>> impulse(sys1),grid
Рисунок 1. Отклик системы на импульсное входное воздействие.
>> step(sys1),grid
Рисунок 2. Реакция системы на единичный скачок входного воздействия.
>> ssys=ss(sys1)
a =
x1 x2 x3 x4
x1 -244.4 -95.68 -26.04 -7.234
x2 64 0 0 0
x3 0 16 0 0
x4 0 0 8 0
b =
u1
x1 8
x2 0
x3 0
x4 0
c =
x1 x2 x3 x4
y1 0 1.543 2.17 0.6028
d =
u1
y1 0
Continuous-time model.
>> initial(ssys,[0 0 0 1],5),grid
Рисунок 3. Собственное движение системы при произвольных начальных условиях.
>> t=0:0.01:40; u=sin(t);lsim(ssys,u,t);grid
Рисунок 4. Реакция системы на входное воздействие произвольной формы, задаваемое в виде вектора его значений во времени.
>> bode(sys1),grid
Рисунок 5. АЧХ и ФЧХ (диаграмма Боде) исследуемой системы
>> nyquist(sys1),grid
Рисунок 6. График АФХразомкнутой системы в полярных декартовых координатах.
>> nichols(sys1),grid
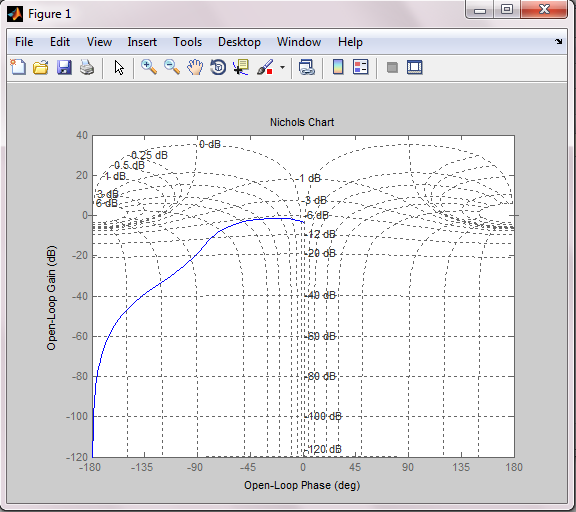
Рисунок 7. Карта Николса (график АФХ разомкнутой системы в декартовых координатах).
>> sigma(sys1),grid
Рисунок 8. График зависимости от частоты сингулярных значений системы.
>> margin(sys1),grid
Рисунок 9. Диаграмма Боде с указанием запасов по амплитуде и фазе.
>> pole(sys1)
ans =
1.0e+002 *
-2.1676
-0.2289
-0.0240 + 0.0249i
-0.0240 - 0.0249i
>> sysz=zpk(sys1)
Zero/pole/gain:
790.1235 (s+20) (s+2.5)
-------------------------------------------
(s+216.8) (s+22.89) (s^2 + 4.798s + 11.94)
>> [z,p,k]=zpkdata(sysz,'v')
z =
-20.0000
-2.5000
p =
1.0e+002 *
-2.1676
-0.2289
-0.0240 + 0.0249i
-0.0240 - 0.0249i
k =
790.1235
>> pzmap(sys1);grid
Рисунок 10. Карты расположения нулей и полюсов системына комплексной плоскости.
Выводы
В результате проделанной работы была создана модель системы слежения с заданными параметрами. Специальные функции средств MATLAB позволили не только быстро и качественно описать САУ, но и провести ряд исследований системы, опирающихся на графическое построение переходных процессов, годографа, оценить временные отклики системы, определить реакцию системы на гармонические воздействия, а также определить полюса и нули системы.
Нули и полюса системы находятся в отрицательной полуплоскости, что говорит об устойчивости рассматриваемой системы.