§ 40. Равновесия в жидких средах

К числу мало изученных относится значительный цикл задачі гидродинамики и механики твердого тела, связанных с проблемой устойчивости в жидких средах. Здесь мы рассмотрим несколько примеров таких задач.

Ртуть над водой. Начнем с простейшего явления. Представим себе, что в сосуде, наполненном водой, над поверхностью воды расположен тонкий слой ртути (рис. 139). Если поверхности воды и ртути — идеальные плоскости, то ртуть будет в равновесии, однако очевид­но, что это равновесие неустойчиво. Ставится вопрос о механизме проникания ртути через воду на дно.

Физически описанное явление можно реализовать еще так: на дно закрытого стакана налить ртуть, а свер­ху нее — воду. Это равновесие устойчиво, но оно поте­ряет устойчивость, если сообщить стакану ускоренное движение вниз, с ускорением в 2—5 раз больше g.

Механизм этого явления был осознан несколько лет то­му назад за рубежом и у нас.

Приведем качественный ответ на поставленный вопрос и его принципиальное обоснование.

Займемся сначала более про­стой моделью, когда толщина слоя ртути равна или больше диаметра стакана. Здесь до­вольно очевидно, что если вследствие случайной асим­метрии в каком-то месте нижней поверхности ртути поя­вится бугорок, то этот бугорок будет расти и он обра­зует в воде воронку, по которой вся ртуть стечет вниз. Последовательные положения ртути и воды в этой постановке можно построить графоаналитическим ме­тодом.

В основной постановке, когда толщина слоя ртути мала сравнительно с диаметром стакана, процесс поте­ри устойчивости и проливания ртути вниз может на­чаться в любой точке поверхности воды. Но влияние этого процесса будет затухать по мере удаления от ме­ста слива по закону

, (1)

где V — скорость жидкости в некоторой точке, V₀ — ско­рость в зоне начала процесса, —толщина слоя ртути и r — расстояние рассматриваемой точки от точки слива (см. § 12).

Таким образом, части ртути, расположенные от точ­ки начавшегося слива на расстоянии более нескольких толщин слоя ртути, будут мало реагировать на начало процесса. Для этих частей найдется более близкий буго­рок, где организуется новый слив.

Поэтому при малой толщине слоя ртути ртуть устре­мится вниз по многим струйкам, расположенным друг от друга на расстоянии порядка (рис. 139).

В эту модель укладывается одно любопытное явле­ние, наблюдаемое при определенных условиях при под­водном взрыве. После взрыва под водой над гладкой поверхностью воды появляется группа фонтанчиков, расположенных друг от друга на одинаковых расстоя­ниях. Дело в том, что когда ударная волна в воде под­ходит к поверхности, то при разгрузке слой воды стремится оторваться от основной массы. Если при этом потенциальная энергия сжатия не достаточна для того, чтобы оторвать слой жидкости от ее основной массы, то мы окажемся в условиях, сходных с условиями ртути на воде, — вместо отрыва получается система фонтан­чиков.

Аналогичное явление можно наблюдать и в металле, когда ударная волна подходит к его свободной поверх­ности. Будет или не будет иметь место описанное явле­ние, зависит от ряда факторов длины ударной волны, кривизны фронта, прочности на разрыв среды и др.

Для количественного исследования описанного здесь явления можно поставить следующую задачу. Пусть слой идеальной несжимаемой жидкости < х < <у < h имеет ускорение а, направленное вертикально вверх. Пусть, далее, верхняя поверхность слоя в мо­мент t = 0 получает малое возмущение = Т₀ sin kx, которое дальше меняется по закону

(x, t) = T(t) sin kx (2)

Требуется найти дальнейшее движение свободной по­верхности.

Если толщина слоя h мала по сравнению с длиной волны возмущения, то уравнения движения можно за­менить приближенными точно так, как это сделано в гл. I для задачи о мелкой воде. Различие будет лишь в том, что ускорение силы тяжести g во всех соотноше­ниях заменится на — (в рассматриваемой здесь задаче ускорение направлено вверх). В частности, для свободной поверхности жидкости получится уравнение.

(3)

Подставляя в него выражение (2), найдем

(4)

откуда

T = A (5)

где А и В — постоянные. Начальные условия для T имеют вид T(0) = Т₀, Т"(0) = , откуда следует, что A 0. Поэтому амплитуда колебаний (2) неограниченно возрастает и движение оказывается неустойчивым.

В нашем приближении неустойчивы возмущения любой длины волны = . В действительности же очень мелкие волны должны затухать вследствие действия сил поверхностного натяжения, и неустойчивыми являются только гармоники, длина волн которых превышает некоторую критическую величину λ_min. Эту величину и следует считать характерным расстоянием между фонтанчиками в рассмотренных здесь явлениях; расчеты [6] дают для нее приближенную формулу

λ_{min = 2 .} (6)

где коэффициент поверхностного натяжения, а p — плотность жидкости.

Образование волн. Проблеме образования ветровых волн посвящено огромное количество статей, обзоров и монографий. Каков механизм образования волн при заданном ветровом режиме, существует ли обратная связь, т. е. влияют ли в свою очередь волны на ветровой режим? Эти и многие другие вопросы не решены до сих пор, хотя качественная картина была ясна уже давно.

Свободная поверхность воды, при наличии над ней воздушного потока, неустойчива: при малых случайных колебаниях давление во впадинах по закону Бернулли больше, чем на выступах, поэтому каждое волновое движение под действием ветра должно прогрессировать. Этот результат легко получить и аналитически (см. например, Ландау и Лифшиц [2]). Если обозначить через V скорость ветра, Р₀ — плотность воды, р - плотность воздуха, λ—длина волны, то рост амплитуды волны определяется множителем , где

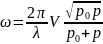(7)

С другой стороны, если высота волны становится порядка своей длины, то гребень волны срывается ветром и преимущества роста приобретают волны большей длины В этих условиях по истечении достаточно большого времени должен наступить установившийся режим. Можно показать, что для этого скорость ветра должна быть вдвое больше скорости волн.

В самом деле, естественно предположить, что здесь (как в задаче обтекания траншеи из § 22) между каждыми двумя соседними горбами волны имеется зона вихревого движения (рис. 140). Перейдем к системе координат, связанной с волной. В этой системе скорость течения жидкости равна скорости движения волны и направлена в отрицательную сторону. В силу не прерывности поля скоростей на границе вихревой зоны скорость ветра тоже должна быть равной С, но направлена в положительную сторону. Переходя снова к неподвижной системе координат, получаем доказательство высказанного утверждения.

Наряду с теоретическими работами проводилось много наблюдений ветровых волн в натурных условиях. Лет 20 назад в Крыму был построен специальный «штормовой бассейн» с вертикальными круговыми цилиндрическими стенками. Над свободной поверхностью там расположено несколько мощных компрессоров, которые способны создавать ветер в большом диапазоне скоростей. Волны в этом штормовом бассейне действительно образуются, но их характер существенно отличен от нормальных ветровых волн, при образовании которых ветер имеет достаточно стабильную направленность. В кольцевом бассейне образовавшиеся волны имея определенную направленность в зоне зарождения, очень быстро переходят в колебания воды в направлении оси бассейна — создаются группы стоячих волн.

Очень интересно наблюдать, но трудно рассчитать явления, которые связаны с кольцевыми волнами. Отметим одно из них — если каким-либо образом, например, шнуровым зарядом ВВ, имеющим форму окружности, создать кольцевую волну (кольцевую выпуклость или кольцевую яму), то в стороны от центра кольца волны будут распространяться с обычным законом затухания. Но в сторону центра длина волны будет меняться медленно, и не будет обычного расщепления волны па более мелкие. В соответствии с этим высота волны при приближении к центру будет нарастать и даст всплеск по высоте, в несколько раз превышающей начальную высоту волны.

Устойчивость струй. В круге идей, рассмотренных выше, имеется большая группа задач по устойчивости жидких струй. Классической является проблема устойчивости водяной струи в воздухе. В частности, если заданы выходная скорость и диаметр струи, то какой высоты можно достигнуть струей? Какого расстояния можно достигнуть струей?

В этих постановках воду можно рассматривать как идеальную жидкость. При скорости струи, близкой скорости звука в воздухе, естественно будет существенным фактор сжимаемости воздуха. До сих пор до конца не решена проблема затопленной струи — водяной струи, движущейся в воде; в этом случае существенным фактором является вязкость, а при значительных скоростях — турбулентность.

Сюда же относится весьма интересная как принципиально, так и с точки зрения приложений проблема устойчивости жидкого стержня при одновременном растяжении и закручивании. Пусть дана осесимметричная рубка из мягкого железа или меди, осевое сечение которой имеет синусоидальный характер; диаметр трубки 10—15 мм, толщина стенки 1—1,5мм.

Опишем, как можно изготовлять такие трубки. Вытачивается матрица, внутренняя поверхность которой совпадает с внешней поверхностью будущей трубки. В мат­рицу вставляется цилиндрическая трубка, которая гер­метически закрыта с одного конца, а с другого конца матрицу нужно завинтить крышкой с небольшим отвер­стием по оси (рис. 141). В это отверстие под большим давлением нагнетается вода, в результате чего внешняя поверхность вставленной трубки вплотную подходит к матрице. При таком способе отштампованная трубка

будет иметь переменную толщину стенок; чтобы избе­жать этого, вставляемый в матрицу цилиндр следует предварительно немного выточить снаружи в нужных местах.

Рассматривается два случая: когда трубка пустая и когда она заполнена водой. В каждом случае трубка растягивается в направлении своей оси и, кроме того, при постоянном растяжении она еще закручивается, причем скорость закручивания меняется. Требуется вы­яснить, в каких случаях волны на поверхности трубки будут сглаживаться (устойчивость) и в каких они будут нарастать (неустойчивость).

Качественно довольно ясно, что при простом растя­жении (или растяжении с достаточно малым закручи­ванием) мы получим устойчивый процесс — волны на поверхности трубки будут сглаживаться. В самом деле, растягивающая сила будет увеличивать диаметр сече­ний трубок в шейках и уменьшать диаметр сечений в пучностях.

Все изменится, если наряду с растяжением трубка достаточно сильно закручивается. Волокна трубки, рас­положенные в ее осевом сечении, превратятся в спи­рали, а растяжение будет сжимать эти спирали, осо­бенно сильно в узких местах, соответствующих шейкам трубки. Это приведет к дальнейшему сжатию шеек, и процесс будет неустойчивым.

Очень желательно построить количественную модель описанного явления. Предварительно следует выяснить статическую и динамическую устойчивость стержней и трубок (упругих и с пластичностью) при чистом закру­чивании. При этом нужно рассмотреть два случая: а) расстояние между торцами трубки или стержня не меняется, б) действуют только крутящие силы.

Взрыв в воде. Здесь будут описаны три явления, наблюдаемых при взрыве в воде. Для них не построено количественных теорий и даже качественно еще не все в них ясно.

1) Выше говорилось о том, что если цилиндриче­скую трубку, заделанную с обеих концов, опустить вер­тикально в воду и под ней произвести взрыв, то трубка обожмется по законам потери ди­намической устойчивости — сечение трубки примет волновой характер, причем частота волн будет убывать но мере удаления от нижнего кон­ца. Это явление мы объяснили про­стой приближенной схемой.

Однако в этом эксперименте об­наруживается еще одно интересное

явление, которое не укладывается в простейшую схе­му,— обжатая трубка (см. рис. 138) имеет вид туго за­плетенной косы! Как объяснить это явление?

2. Возьмем сферическую оболочку из упругого ма­териала (например, надутый воздухом мяч) и погрузим ее в резервуар с водой, в котором можно создавать большие давления (рис. 142). Считая, что материал ста­новится пластичным за пределами упругости, найти по его характеристикам: а) критическое давление, при ко­тором происходит потеря упругости, б) форму сфериче­ской оболочки после того, как она потеряет устойчи­вость, в) форму потери устойчивости в случае, если дав­ление в воде мгновенно превысит в п раз критическое.

Словом, задача состоит в том, чтобы перенести на случай сферической оболочки схемы статической и ди­намической неустойчивости, которые выше рассматрива­лись для случая стержней (в связи с этим см. [8]).

2. В одной из стенок толстостенного бака имеется круглое отверстие, в которое можно вставлять тонкие мембраны различной толщины и из разных материалов (железо, медь, свинец и др.). В центре бака, против за­крытого мембраной отверстия, производятся взрывы различной мощности, причем после каждого взрыва прогнутая мембрана заменяется новой (рис. 143).

В одной серии опытов был обнару­жен следующий парадоксальный эф­фект. При увеличении заряда прогиб мембраны увеличивался до определен­ной величины, а при дальнейшем уве­личении заряда прогиб еще увели­чился, но изменил направление — мем­брана оказывалась прогнутой навстре­чу взрыву!

Качественно явление можно объяснить так. При по­тере устойчивости под действием взрыва па мембрану (как и на стержень, случай которого был рассмотрен в начале главы) действует сила F не только переменной величины, но и переменного направления. Когда F на­правлена во внешность бака, она дает прогиб вовне, а когда внутрь, то и мембрана прогибается вовнутрь. Для построения схемы этого явления нужно прежде всего изучить вопросы потери устойчивости круговых мембран, закрепленных на краю.