
Литература
А. Н. Тихонов и А. А. Самарски й, Уравнения математической физики, «Наука», М., 1966.
В. С. Владимиров, Уравнения математической физики, изд. 2-е, «Наука», М., 1971.
3 Л. Д. Ландау и Е. М. Л и ф ш и и, Механика сплошных сред, ГИТТЛ, М, 1954.
Г. Л а м б, Гидродинамика. ГИТТЛ, М. — Л., 1947.
Л. А. Вулис, В. П. Каш кар о в, Теория струй вязкой жидкости, «Наука», М., 1965.
А. А. Л у г о в ц о в, Б. А. Л у г о в ц о в, В. Ф. Тарасов, О движении турбулентного вихревого кольца, В сб «Динамика сплошной среды», вып. III, Новосибирск, 1969.
Б. А. Л у г о в ц о в, О движении турбулентного вихревого кольца и переносе им пассивной примеси, В сб. «Некоторые проблемы математики и механики» (к семидесятилетию М. А. Лаврентьева), «Наука», Л., 1970.
А. Т. Онуфриев, Теория движения кольца под действием силы тяжести. Подъем облака атомного взрыва, ПМТФ, 2 (1967).
А. А. Л у г о в ц о в, Б. А. Л у г о в ц о в, Пример обтекания тела с движущейся границей, В сб. «Динамика сплошной среды», вып.
УШ, Новосибирск, 1971.
§ 38. Неустойчивость стержней Статическая и динамическая потери устойчивости.
 Простейший
эксперимент, поясняющий различие между
этими двумя формами потери устойчивости
стержней, можно поставить так. Пусть
стержень (т. е. упругая тонкая полоса)
расположен вертикально, его нижний
конец закреплен в твердом основании,
а сверху на него действует не слишком
большая вертикальная сила F(рис.
135). Если стержень немного отклонить от
вертикального положения и затем
отпустить, то он будет совершать
затухающие колебания вокруг положения
равновесия и через некоторое время
вернется в это положение. Мы имеем
случай устойчивого равновесия.
Простейший
эксперимент, поясняющий различие между
этими двумя формами потери устойчивости
стержней, можно поставить так. Пусть
стержень (т. е. упругая тонкая полоса)
расположен вертикально, его нижний
конец закреплен в твердом основании,
а сверху на него действует не слишком
большая вертикальная сила F(рис.
135). Если стержень немного отклонить от
вертикального положения и затем
отпустить, то он будет совершать
затухающие колебания вокруг положения
равновесия и через некоторое время
вернется в это положение. Мы имеем
случай устойчивого равновесия.
Будем теперь постепенно увеличивать силу F. С ростом F частота колебаний уменьшается, и при некотором значении F = Fкр частота обратится в нуль — стержень будет находиться в состоянии безразличного равновесия. При дальнейшем увеличении силы F равновесие становится неустойчивым: после любых отклонений стержень изгибается и не возвращается в вертикальное положение
Величина критической силы Fкр, при которой равновесие перестает быть устойчивым, зависит от формы, размеров и упругих свойств стержня, а также от условий его закрепления (граничных условий). Описанный выше процесс потери устойчивости, при котором величина нагрузки постепенно увеличивается до тех пор, пока она не достигнет критического значения, называется статической потерей устойчивости.
Иначе ставится эксперимент по динамической потере устойчивости. Здесь в некоторый момент времени стержень немного изгибается, и к нему сразу прикладывается вертикальная сила, величина которой превышает критическую. Оказывается, что в этой постановке потеря устойчивости происходит иначе, чем при статическом нагружении. Ниже мы рассмотрим это различие подробнее.
В механике упругих тел большинство изученных задач относится к случаю статической устойчивости. Наиболее классическая из таких задач была решена Л. Эйлером еще в 1744 году.
 Задача
Эйлера. Пусть
концы стержня закреплены шарнирно,
причем нижний шарнир неподвижен, а
верхний может перемещаться вертикально;
к верхнему концу прикладывается
вертикальная сила F
(рис. 136). Предположим, что сечения стержня
одинаковы, длина его равна l,
момент инерции J
и модуль Юнга Е.
Задача
Эйлера. Пусть
концы стержня закреплены шарнирно,
причем нижний шарнир неподвижен, а
верхний может перемещаться вертикально;
к верхнему концу прикладывается
вертикальная сила F
(рис. 136). Предположим, что сечения стержня
одинаковы, длина его равна l,
момент инерции J
и модуль Юнга Е.
При равновесии в каждом сечении стержня изгибающий момент упругих сил должен равняться моменту силы F относительно середины изогнутого стержня. Момент упругих сил, как известно, пропорционален кривизне стержня k(х) в рассматриваемом сечении и равен ± EJk, а момент силы F в этом сечении равен ± Fу.
Задачу
будем решать в линейном
приближении,
предполагая, что прогибы стержня малы.
Тогда кривизна
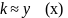 ,
и мы получаем уравнение равновесия
в виде
,
и мы получаем уравнение равновесия
в виде

(знак выбран с учетом того, что у" > 0 при « y<0 и наоборот).
Общее решение уравнения (1) имеет вид

где A и В — произвольные постоянные, а

Условие шарнирного закрепления концов приводит к граничным условиям

 (4)
(4)
из которых следует, что В = 0 и

Если
F
<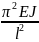 , то из (5) следует что A
= 0, т.е. при этом условии возможно лишь
тривиальное решение
, то из (5) следует что A
= 0, т.е. при этом условии возможно лишь
тривиальное решение
 Если
же F
Если
же F
 ,
то при условии
,
то при условии
 ,
которое переписывается в виде
,
которое переписывается в виде

(п — произвольное целое число), кроме тривиального, возможны еще решения вида

Мы получаем спектр собственных значений (6) величины F, каждому из которых соответствует искривленная равновесная форма стержня (7). Критической силой естественно считать ту, при которой перестает быть устойчивой первоначальная прямолинейная форма стержня. Очевидно, эта сила соответствует значению п=1 и равна

она
называется эйлеровой
силой.
При медленном возрастании нагрузки
F
потеря
устойчивости происходит при этом
значении
 .
Стержень при этом изогнется в форме
одной полуволны синусоиды, и если
произойдет излом, то стержень распадется
на два куска.
.
Стержень при этом изогнется в форме
одной полуволны синусоиды, и если
произойдет излом, то стержень распадется
на два куска.
Отметим,
что величина А
амплитуды прогиба стержня в приведенном
выше решении задачи Эйлера никак не
определяется и теоретически может быть
сколь угодно большой. Этот противоречащий
действительности вывод является
следствием линеаризации задачи. На
самом деле при больших прогибах перестает
быть обоснованным приближенное
выражение для кривизны, которым мы
пользовались при выводе уравнения (1).
В этом случае надо использовать точное
выражение
 ,
и задача становится нелинейной.
Исследование устойчивости в нелинейной
постановке также возможно, оно дает и
конкретные результаты, но основные
выводы остаются примерно теми же, что
и в линейной постановке. На конгрессе
механиков в Калифорнии
(1968 г.) этим проблемам был посвящен
обзорный доклад французского ученого
Л. Готье).
,
и задача становится нелинейной.
Исследование устойчивости в нелинейной
постановке также возможно, оно дает и
конкретные результаты, но основные
выводы остаются примерно теми же, что
и в линейной постановке. На конгрессе
механиков в Калифорнии
(1968 г.) этим проблемам был посвящен
обзорный доклад французского ученого
Л. Готье).
Динамическая постановка. При изучении действия взрыва на стержни и оболочки были обнаружены формы потери устойчивости, которые не укладываются в разобранную статическую схему .Представим себе следующий эксперимент.
Пусть имеется стержень, расположенный вертикально и закрепленный так же, как в предыдущей задаче. Мы предположим, что разрушение стержня наступает при малых деформациях, когда еще применима линейная теория. Пусть сверху к стержню мгновенно прилагается вертикальная сила F величина которой в несколько раз превышает Эйлерову силу . Нужно выяснить, как будет происходить потеря устойчивости стержня и его разрушение.
Как
мы видели выше, в схеме статического
нагружения стержень разламывается
на два куска. Опыт показывает, что в
принятых здесь условиях стержень
разламывается на несколько кусков,
число которых зависит от отношения
 .
Нашей задачей является выяснение
движения стержня в начальный отрезок
времени и определение числа кусков,
па которые он разламывается.
.
Нашей задачей является выяснение
движения стержня в начальный отрезок
времени и определение числа кусков,
па которые он разламывается.
Как известно, уравнение малых движений стержня описывается дифференциальным уравнением
 (9)
(9)
где
 — плотность материала и S
— площадь поперечного сечения
стержня; функция f
определяется начальным искривлением,
поперечной нагрузкой и т. п.
— плотность материала и S
— площадь поперечного сечения
стержня; функция f
определяется начальным искривлением,
поперечной нагрузкой и т. п.
Решение этого уравнения, удовлетворяющее граничным условиям (4), к которым теперь следует добавить у"=0 при х=0,l (в статической схеме эти условия выполнялись автоматически), естественно искать в виде ряда Фурье по синусам:

Если
правая часть уравнения (9) также
представлена рядом Фурье
 ,то при
подстановке (10) в это уравнение мы получим
систему обыкновенных уравнений
,то при
подстановке (10) в это уравнение мы получим
систему обыкновенных уравнений

где
 Величина
qk
представляет
собой амплитуду той гармоники
Величина
qk
представляет
собой амплитуду той гармоники

которой соответствует изгиб стержня по синусоиде с k полуволнами.
Уравнение
(11) показывает, что при
 закон изменения
закон изменения
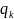 - синусоидальный, поэтому соответствующие
гармоники
- синусоидальный, поэтому соответствующие
гармоники
 имеют
ограниченную амплитуду и не дают
потери устойчивости. При
имеют
ограниченную амплитуду и не дают
потери устойчивости. При
 ,
напротив, решения уравнения (11) имеют
непериодический характер:
,
напротив, решения уравнения (11) имеют
непериодический характер:

где

(мы
считаем, что
 = 0
= 0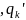 (0)
== 0). С течением времени амплитуды
соответствующих гармоник неограниченно
возрастают, причем быстрее всего
возрастает амплитуда той гармоники,
для которой величина
(0)
== 0). С течением времени амплитуды
соответствующих гармоник неограниченно
возрастают, причем быстрее всего
возрастает амплитуда той гармоники,
для которой величина
 —
наибольшая. Из (15) видно, что максимум
достигается при
—
наибольшая. Из (15) видно, что максимум
достигается при
 ,
так что наибольшую неустойчивость
дает синусоидальная форма стержня с
числом полуволн, равным ближайшему
целому k
числу
,
так что наибольшую неустойчивость
дает синусоидальная форма стержня с
числом полуволн, равным ближайшему
целому k
числу

Естественно ожидать, что если стержень не выдержит нагрузки и сломается, то число изломов будет равно именно этому числу.
К тому же выводу можно прийти и из энергетических соображений. Существует принцип, согласно которому движение консервативной механической системы осуществляется так, чтобы в каждый данный момент ее полная потенциальная энергия была возможно меньшей. (Скажем, в примере, которым начиналась глава, шарик скатывается по желобку на сферической поверхности, если такой желобок есть.)
Подсчитаем полную потенциальную энергию стержня в нашей задаче. Она составляется из энергии упругого изгиба стержня
П1=
и потенциала внешних сил П2 (продольным сжатием стержня и его начальным изгибом мы пренебрегаем). Потенциал П2 равен работе силы F с противоположным знаком: П2 = —F l, где l — смещение верхнего конца стержня по вертикали. Предполагая стержень нерастяжимым и обозначая через l0 его длину, а через l — проекцию его верхнего конца на ось х, будем иметь

Так
как
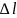 =
l0
— l,
то мы получим
=
l0
— l,
то мы получим
П2=
а значит,
П = П1
+ П2
=
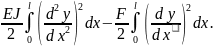 (17)
(17)
Отсюда с учетом формул (12) получаем выражение полной потенциальной енергии для гармоники (13) :
П
=
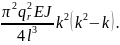 (18)
(18)
Мы видим, что минимальное значение П достигается для той гармоники уk, номер которой равен ближайшему целому к числу (16), т. е. той самой гармонике, которая дает наибольшую неустойчивость.
Таким образом, мы двумя способами пришли к одному и тому же выводу: когда к стержню мгновенно прикладывается нагрузка F в п раз превышающая критическую эйлерову силу Fкр, то стержень изгибается

по
синусоиде с числом полуволи, равным
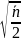 или ближайшему целому числу; если
стержень при этом разрушается, то число
изломов также оказывается равным
или ближайшему целому числу; если
стержень при этом разрушается, то число
изломов также оказывается равным
этом числу.
На рис. 137 приведены фотографии эксперимента, иллюстрирующего изгиб стержня при динамической нагрузке и его разрушение на несколько кусков 1). Конечно, на практике наш вывод осуществляется лишь в вероятностном смысле: при проведении большого числа опытов среднее число осколков близко к .
Интересно отметить, что аналогичный результат наблюдается при мгновенном нагружении тонкостенной рубки, когда эта трубка подвергается внешнему давлению. Так же, как в случае стержня, имеется критическое давление Fкр такое, что если внешнее давление на трубку меньше критического, то трубка устойчива; если сжать ее в пределах упругости, то при снятии сжимающей силы она вернется в прежнее состояние. Если же давление превысит критическое, то трубка потеряет устойчивость в прежнем смысле.
Рис.
138.

 .
.
Наиболее яркий пример динамической неустойчивости дает следующий опыт. Если тонкостенную трубку с заделанными концами погрузить в воду, а затем вблизи нижнего конца произвести взрыв, то трубка будет обжата так, что ее сечение будет волнистым с наибольшим количеством волн вблизи заряда (рис. 138).
Хотя за последние 20 лет проблема динамической устойчивости значительно продвинулась, все же здесь осталось еще много нерешенных задач: динамическая устойчивость труб при осевой нагрузке, динамическая неустойчивость сферических оболочек и многие другие.
