
2-й семестр / Семинар 6
.pdf
1
Вопросы задаем в чате группы в вацапе, решения выкладываем там же
«Интегрирование иррациональных функций»
Таблицу переписать в тетрадь и выучить
теоретический материал по теме «Интегрирование иррациональных функций» предлагаем структурировать в виде таблицы, объединяющей наиболее часто встречающиеся случаи интегрирования функций, содержащих иррациональность. Каждому виду интеграла предлагается замена переменной, приводящая подынтегральную функцию к рациональной или тригонометрической функции, интеграл от которой легче приводится к
табличному интегралу. |
|
|
|
|
|
|
|
|
|
|
|
Введем |
обозначения: |
пусть ( )- |
функция, |
содержащая |
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
иррациональные выражения, например |
|
|
√2 − 2, √2 + 2 |
и т.д. В |
|||||||
√, |
|||||||||||
зависимости от вида иррациональности при интегрировании ( ) удобно воспользоваться одной из следующих подстановок, в результате которой
получаем функцию, которая является рациональной или тригонометрической.
№
I a
I b
II
Вид
интеграла
R(x, n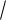 x)dx
x)dx
R(x, n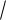 x, m
x, m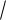 x)dx
x)dx
|
|
|
|||
|
|
|
ax b |
|
|
|
|
|
|
||
|
R x, n |
|
|
dx |
|
|
|
cx d |
|||
Таблица 1. Интегрирование некоторых алгебраических иррациональностей
|
|
Замена |
|
|
|
Интеграл, к которому |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
сводится исходный |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
n R(t |
n |
,t)t |
n 1 |
|
|
|
|
|||||||||
x t |
n |
|
dx |
nt |
n 1 |
|
|
|
|
|
dt |
|
|
|||||||||||||
|
, |
|
dt |
|
|
|
|
F(t)dt |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x t |
k |
, dx |
kt |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
, где k есть |
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
наименьшее общее |
k R(t |
k |
,t |
|
,t |
|
|
)t |
k 1 |
|
|
|
|
|
|
|||||||||||
|
n |
m |
|
|
dt F(t)dt |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
кратное показателей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
радикалов n |
и m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ax b |
t |
n |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b t |
|
d |
|
|
||||
|
cx d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,t |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
b tnd |
|
|
n(ad cb) R |
n |
c a |
|
||||||||||||||||
|
x |
, |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
||||||||||
|
tnc a |
|
|
|
t n 1 |
|
|
|
dt |
F(t)dt |
|
|||||||||||||||
dx |
ntn 1(ad cb) |
dt |
(t nc a)2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
(tnc |
a)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

2
|
|
|
|
|
|
|
|
|
|
|
x a sint |
или |
|
|
|
|||||||
III |
|
R(x, |
|
a |
2 |
x |
2 |
)dx |
|
|
x a cost |
F(sint,cost)dt |
||||||||||
|
dx a costdt или |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx a sintdt |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x a tgt |
или |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a ctgt |
|
|
|
|||||||
IV |
R(x, |
|
a |
2 |
x |
2 |
)dx |
dx |
|
|
|
a |
dt или |
F(sint,cost)dt |
||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
t |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
a |
dt |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x cost |
или |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
V |
|
R(x, |
|
x |
2 |
a |
2 |
)dx |
|
|
|
x sin t |
|
F(sint,cost)dt |
||||||||
|
|
|
|
|
|
a sin t |
|
|||||||||||||||
|
|
|
dx |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
dt или |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
t |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
dx |
|
a cost dt |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
В выражении |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ax |
2 |
bx c |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
выделяем полный |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
квадрат: |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
ax |
2 |
bx c |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
a(x |
|
b )2 b2 c |
|
|
||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
2a |
|
4a |
|
|
|
||||
|
|
|
|
|
|
, |
x |
b |
|
|
t , dx dt |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||||||||
|
|
|
2 |
|
|
|
2a |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
VI |
|
|
ax |
bx c |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a 0 |
|
|
|
|
обозначим |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
2 |
bx |
c |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ax |
|
0 |
1 |
b c p2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
4a |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
1 |
dt |
|
|
|
|
|
|
|
|
|
|
Если |
|
|
c 0 |
|
a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4a |
|
t2 p2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
1 |
dt |
|
|
|
|
|
|
|
|
|
|
Если |
|
|
c 0 |
|
a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4a |
|
t2 p2 |
|||||||||

VII
VIII
|
|
|
dx |
|
2 |
, |
|
|
|
bx c |
|
ax |
|||
|
|
a 0 , |
|
ax |
2 |
bx c 0 |
|
|
|||
|
|
dx |
|
2 |
|
x |
|
|
|
ax bx c |
|
ax |
2 |
bx c 0 |
|
В выражении
ax |
2 |
bx c , как и |
|
выше, выделяем полный квадрат и делаем замену
x |
|
b |
|
t , dx dt |
|||||
2a |
|||||||||
|
|
|
|
|
|
||||
1 |
|
обозначим |
|
||||||
|
|
b |
2 |
|
|
||||
|
|
|
|
|
c p |
||||
|
|
|
|
|
|
|
2 |
||
a |
|
4a |
|
||||||
|
|
|
|
||||||
x |
1 |
, dx |
dt |
||
t |
t |
2 |
|||
|
|
||||
|
|
|
|||
|
|
|
|
||
3
1 |
|
|
dt |
|
|||
a |
p |
2 |
t |
2 |
|||
|
|||||||
|
|
|
|
||||
arcsin |
t |
|
C |
|
|||
p |
|
||||||
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
dt |
|
|
1 |
a |
|
b |
t |
2 |
|||||
|
|
c |
|
|||||||
|
|
|
||||||||
|
t |
t |
2 |
t |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dt |
|
|
|
||
|
|
ct |
2 |
bt a |
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||
И интеграл сводится к случаям
VI или VII
Таблица 1. помогает научиться правильно классифицировать тип интеграла от функции, содержащей иррациональное выражение.
Все примеры нужно разобрать
Это значит, решаем примеры в тетрадке , разбираем. Если есть вопросы задаем в чате группы в вацапе
Проиллюстрируем на примерах интегрирование алгебраических иррациональностей

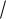 x
x
Пример I b. Вычислить интеграл x 3 x2 dx .
Решение:
После рассмотрения подынтегральной функции получаем, что: данный интеграл относится к типу I b , так как подынтегральная функция содержит радикалы с разными показателями n=2 и m=3
4
|
|
|
|
|
|
|
|
|
|
|
НОК(2;3) 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
|
|
dx |
|
x t |
6 |
|
|
|
|
|
|
|
|
|
t |
3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
t |
4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6t |
dt 6 |
|
|
|
dt |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
6 |
t |
4 |
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
t |
1 |
|||||||||||
|
|
|
|
|
|
|
|
dx |
6t |
5 |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6 t |
|
1 dt 6 |
|
|
dt |
|
|
|
|
t |
3 |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
dt |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
= 6 |
|
|
|
t |
|
6 |
|
|
|
|
|
|
6 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(t 1)(t 1) |
|
3 |
|
|
|
|
|
|
|
|
2(t 1) |
|
|
|
|
2(t 1) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2t |
3 |
6t 3ln t 1 |
3ln t 1 C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
x 1 |
|
|
|
|
|
|
|
|
|
|||||
2t |
3 |
6t 3ln |
C 2 |
|
3 |
|
x 3ln |
|
|
|
C |
|
|
|
|
|
|
|||||||||||||||||||||||
|
t 1 |
|
x 6 |
|
|
6 |
|
x 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
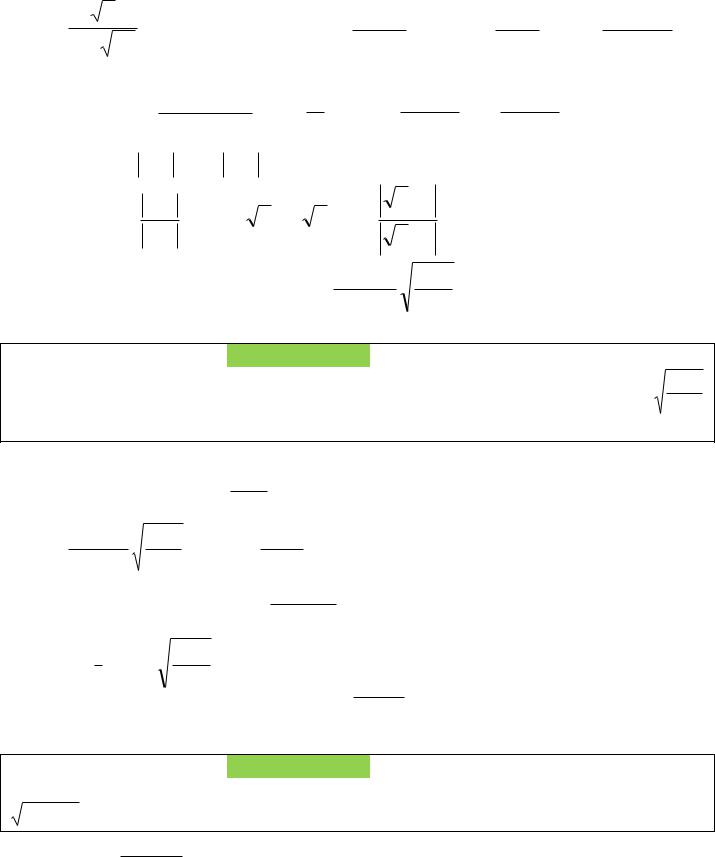
Пример II. Вычислить интеграл |
|
|
|
|
1 |
|
|
|
|
|
1 x |
dx |
. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
(1 x) |
2 |
|
|
1 x |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
t |
4 |
1 1 |
|
|
6 |
|
dt |
|||
|
t |
2 |
1 |
||
|
|
|
|||
|
|
|
|
||
Решение.
После рассмотрения подынтегральной функции получаем, что: данный интеграл
относится к типу II, так как подынтегральная функция содержит радикал вида |
1 |
x |
|
1 |
x |
||
|
с показателем n=2
t
|
|
|
|
|
1 x |
t |
2 |
|
|
|
|||
|
|
|
|
|
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
1 x |
|
|
|
1 t |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
(1 |
x) |
2 |
1 x |
dx x |
1 |
t |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
4t |
|
|
|||
|
|
|
|
|
|
dx |
|
|
|||||
|
|
|
|
|
|
(1 t |
2 |
) |
2 |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
dt |
|
1 |
C |
1 x |
C |
|
|
|
|||
2 |
|
t |
|
1 x |
. |
|
|
|
|||
|
|
|
|
Пример III. Вычислить интеграл
Решение.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t |
2 |
2 |
|
|
4t |
|
|
|
|
|
|
|
t |
|
|
dt |
|||
|
|
|
|
|
1 t2 |
|||||
4t |
4 |
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
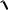
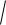 9 x2 dx .
9 x2 dx .
После рассмотрения подынтегральной функции получаем, что: данный интеграл относится к типу III, так как подынтегральная функция содержит радикал вида
a |
2 |
|
x |
2 |
|
, где a 3.
R(x, 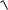
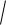 a2 x2 )dx
a2 x2 )dx

5
|
|
|
|
|
2 |
x 3sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
9 x |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dx 3costdt |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
9 9sin |
2 |
t 3costdt 9cos |
2 |
tdt |
9 |
(1 cos 2t)dt |
||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9 |
t |
9 |
sin 2t C |
9 |
|
x |
|
9 |
|
|
|
|
|
x |
|
C |
. |
|
|||||||
|
|
|
arcsin |
|
|
|
|
|
arcsin |
|
|
|
|
||||||||||||
|
|
|
|
|
|
sin 2 |
|
|
|
|
|
||||||||||||||
2 |
|
4 |
|
|
|
|
|
2 |
|
3 |
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
||
|
Пример IV. Вычислить интеграл |
|
|
|
|
dx |
|
|
|
||||||||||||||||
|
(25 x |
2 |
) |
|
25 x |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение.
.
После рассмотрения подынтегральной функции получаем, что: данный интеграл относится к типу IV, так как подынтегральная функция содержит радикал вида
a |
2 |
x |
2 |
|
|
, где
a
5
.
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
x 5tgt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
(25 x |
2 |
) |
25 x |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
cos |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
||||||||||||||||||||
(25 25tg 2t) |
|
|
|
|
|
|
|
|
|
|
|
cos2 t |
25 |
|
|
|
|
|
|
|
|
|
|
|
cos2 t |
||||||||||||||||||||||||||
25 25tg 2t |
(1 |
|
sin 2 t |
) |
1 |
sin 2 t |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 t |
cos2 t |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
dt |
1 |
|
costdt |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
25 |
|
|
|
|
|
||||||||||||||
2 |
t sin |
2 |
t |
|
|
cos |
2 |
t sin |
2 |
t |
cos |
t |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
cos2 t |
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
sin t C |
1 |
|
|
x |
C |
|
|
|
|
|
sin arctg |
|
|
|||
|
|
|
|
|
|||||
|
25 |
|
25 |
|
5 |
|
|||
Пример V. Вычислить интеграл

x |
2 |
16 |
|
||
|
x |
3 |
|
|
dx
.
Решение.
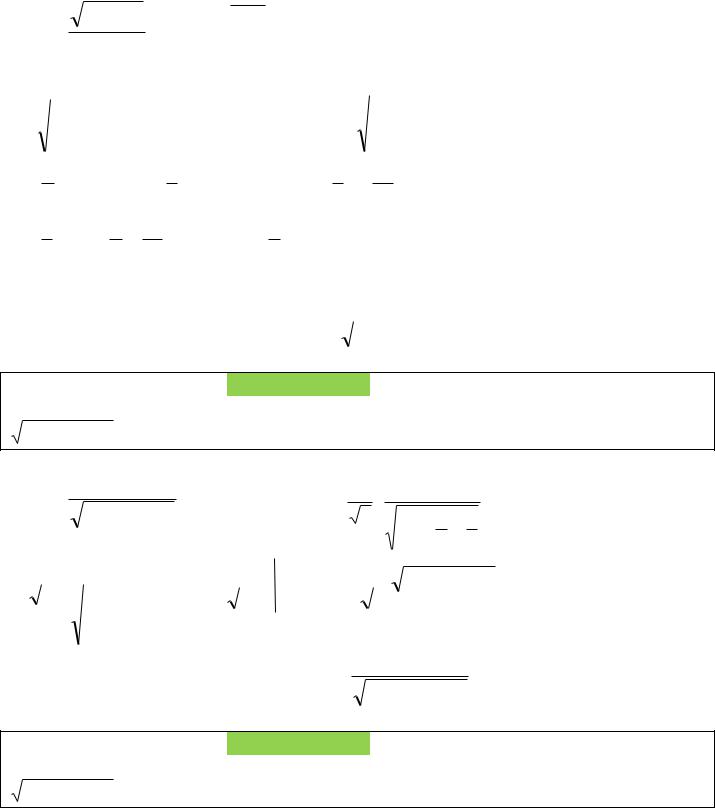
После рассмотрения подынтегральной функции получаем, что: данный интеграл
относится к типу V, так как подынтегральная функция содержит радикал вида |
x |
2 |
a |
2 |
|
|
, где a 4.
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x |
2 |
16 |
|
|
|
|
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
4cost |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin3 t |
|
|
|
4cost |
|
|
|
|
|
|
|
1 sin 2 t |
|
sin3 t |
cost |
|||||||||||||||
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|||||||||||
|
|
sin 2 t |
|
|
|
|
|
|
sin 2 t |
|
|
|
sin 2 t |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
sin 2 t |
|||||||||||||||||||
|
1 |
cos |
2 |
tdt |
1 |
(1 cos 2t)dt |
1 |
t |
1 |
sin 2t C |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
4 |
|
|
8 |
8 |
16 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
4 |
|
|
1 |
|
|
|
|
|
|
|
|
4 |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
arcsin |
|
|
|
|
|
|
|
|
|
arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
8 |
|
|
|
|
x |
|
|
16 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Пример VI. Вычислить интеграл |
|
|
|
|
|
1 |
|
|
dx . |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2x2 x 3 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение.
После рассмотрения подынтегральной функции получаем, что: данный интеграл относится к типу VI, так как подынтегральная функция содержит радикал вида
ax |
2 |
|
bx c
, где
a 2 0 ,
b 1,
c 3.
|
|
1 |
dx a 2, a 0 |
|
2 |
x 3 |
|||
2x |
|
|||
|
|
|
1 |
|
|
1 |
|
dx |
|
|
|
|
|
|
|||
|
2 |
x |
2 |
|
x |
|
3 |
|
|
|
|
||||
|
|
|
2 |
2 |
|||
|
|
|
|
|
|
||
|
1 |
|
|
|
|
dx |
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
2x |
|
x |
||||
2 |
|
1 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
23 |
|
|
2 |
|
|
4 |
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
4 |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Пример VII. Вычислить интеграл |
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
5 2x 3x |
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение.
3 C .
C .
dx.
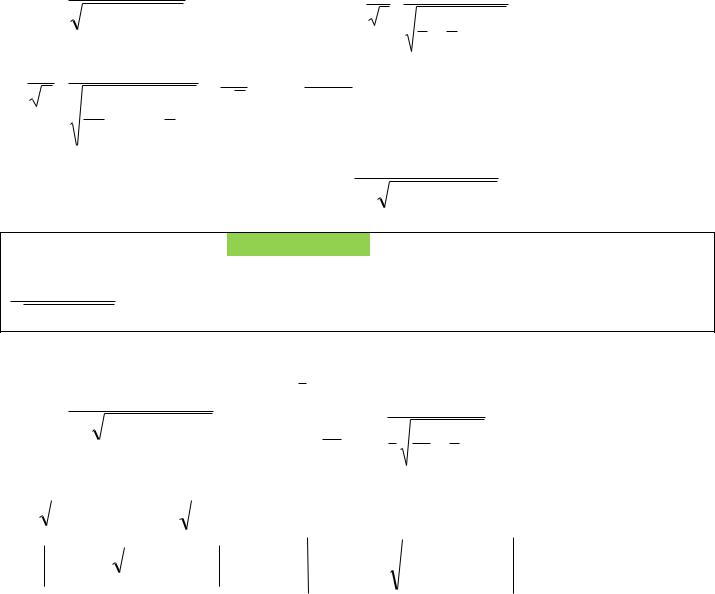
После рассмотрения подынтегральной функции получаем, что: данный интеграл относится к типу VII, так как подынтегральная функция содержит радикал вида
ax |
2 |
|
bx c
, где a 3 0 , b 2, c 5.
7
|
1 |
dx a 3, a 0 |
5 2x 3x2 |
|
1 |
|
|
|
1 |
|
dx |
3 |
5 |
|
2 |
|
|||
|
|
|
x x |
2 |
|||
|
|
|
|
|
|||
|
|
|
3 |
3 |
|
||
|
|
|
|
|
|
|
1 |
|
dx |
|
|
|
3 |
|
|
|
2 |
||
|
16 |
1 |
||||
|
|
|
||||
|
|
|
x |
|
|
|
|
|
9 |
|
3 |
|
|
1 
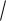 3
3
arcsin |
3x 1 |
C |
|
4 |
|||
|
|
.
Пример VIII. Вычислить интеграл |
|
1 |
dx |
. |
|
2 |
|||
x |
10x |
6x 1 |
|
|
|
|
Решение.
После рассмотрения подынтегральной функции получаем, что: данный интеграл относится к типу VIII, так как подынтегральная функция содержит дробь вида

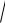 ax2
ax2
1bx c
, где
a
10
,
b
6
,
c
1
.
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
t |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
||||
|
|
10x |
|
|
|
6x 1 |
|
|
|
|
|
|
|||||
|
|
x |
2 |
|
|
|
dx |
dt |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
t |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10 6t t2 |
(t 3)2 1 |
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
dt |
||
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
10 |
|
6 |
|
|
t |
|
||
|
|
1 |
|
|||||||
|
t |
t |
2 |
t |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
ln t 3 |
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
||||||
t |
|
6t 10 C ln |
|
3 |
|
|
6 |
|
10 |
C . |
|||
|
|
x2 |
x |
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|||
Примеры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
∫ 2 2 = |
|||||||||||||||||||||
1. ∫ |
√ 2 − 2 = | |
|
|
| = ∫ √2(1 − 2 ) = |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
∫(1 + 2) = |
+ |
2 + = |
|
+ |
|
√ |
|
2 |
− |
2 |
+ |
|||||||||||||||||||||||||||||
|
2 |
2 |
4 |
2 |
|
|
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2. ∫ |
|
|
|
|
|
|
= | = |
|
|
| = ∫ |
|
|
|
|
|
|
|
∙ |
|
|
|
|
= |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||
|
|
|
√ |
2 |
+ |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√1 + |
|
|
|
|
|
|
|
|
|
|||||||||||||||||

8
|
|
|
= ∫ |
|
|
= ∫ |
|
= ∫ |
( ) |
|
= | = |
| = ∫ |
|
= |
||||||||||||||||||||||
|
|
|
|
|
|
2 |
1 − 2 |
|
1 − 2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
1 |
|
1 |
+ |
||||||||||||||||
= ∫ ( |
|
|
+ |
|
) |
|
|
= − |
|
(1 |
− ) + |
|
|
(1 + ) + С = |
|
|
( |
|
|
|
) + С = |
|||||||||||||||
1 − |
1 + |
2 |
2 |
2 |
2 |
1 |
− |
|||||||||||||||||||||||||||||
|
1 |
|
|
|
|
(1 + )2 |
|
|
|
1 |
(1 |
+ )2 |
|
|
|
1 + |
|
|
|
|||||||||||||||||
= |
|
( |
|
) + С = |
|
|
( |
|
|
) + = ( |
|
|
|
) + = |
||||||||||||||||||||||
2 |
(1 − ) ∙ (1 + ) |
2 |
1 |
− 2 |
|
|
|
|||||||||||||||||||||||||||||
=( + ) + = (√1 + 2 + ) + =
= (√1 + ( |
|
|
2 |
|
|
|
|
|
|
) + = (√ + 2 |
|
||||||
|
) |
+ |
|
+ ) − + = |
||||
|
|
|||||||
|
|
|
|
|
|
|||
= ( + √ + 2 + ) +
Интегрирование гиперболических функций Интегрируя гиперболические функции, так же как и в случаи
тригонометрических функций, используем формулы например:
|
|
2 − 2 = 1 или |
|||||
2 = |
1 |
(2 − 1) |
2 = |
1 |
(2 + 1) |
||
|
|
|
|||||
2 |
2 |
||||||
|
|
|
|
||||
2 = 2
Два Важных интеграла
Рассмотрим два способа, интегрирования наиболее часто встречающегося интеграла
+ ∫  , при условии 2 − < 0 или − 2 > 0,
, при условии 2 − < 0 или − 2 > 0,
√2 + 2 +
Идея интегрирования состоит в том, что исходный интеграл путём алгебраических преобразований числителя приводится к сумме двух интегралов, которые легко берутся.
|
|
+ |
( 2 + 2 + ) |
|
( + ) |
|||||
∫ |
|
|
= ∙ ∫ |
|
|
|
+ ∙ ∫ |
|
|
= |
|
|
|
|
|
|
|
||||
|
√2 + 2 + |
√2 + 2 + |
√( + )2 + ( − 2 ) |
|||||||
= ∙ 2 ∙ √2 + 2 + + ∙ | + + √2 + 2 + | + .
Рассмотрим два способа, позволяющие упростить нахождение этих коэффициентов:
первый способ - это подбор коэффициентов по определенному алгоритму, не требующему «изобретательности» от студентов и облегчающий усвоение материала,
9
второй способ - эта замена в интеграле, приводящая к распаду интеграла на два берущихся интеграла.
Для наглядности рассмотрим следующий пример интегрирования интеграла:
|
|
|
3 + 5 |
||
∫ |
|
|
|
|
|
|
|
|
|
||
√ 2 |
+ 6 + 13 |
||||
|
|
Первый способ нахождение коэффициентов происходит по заданному |
|||
алгоритму. Приведем этот алгоритм. |
|||||
|
|
Суть алгоритма состоит в следующем - приравнять числитель исходной дроби к |
|||
производной знаменателя, умноженной на неизвестный коэффициент A и прибавить неизвестный коэффициент B. Тем самым исходный интеграл, распадается на два
интеграла, которые легко приводятся к табличным. Методом неопределенных |
|
|||||
коэффициентов находим неизвестные A и B. |
|
|
|
|
|
|
+ = ∙ ( 2 + 2 + )′ + или |
|
|
|
|
|
|
|
= 2 ∙ |
|
= |
|
|
|
+ = ∙ (2 + 2 ) + => { |
=> { |
|
|
= |
||
2 |
||||||
= ∙ 2 + |
|
= − ∙ 2 |
|
|||
|
|
|
|
|||
= /2 > { = − ∙
3 + 5
Рассмотрим наш пример ∫  √ 2 + 6 + 13
√ 2 + 6 + 13
3 + 5 = ∙ ( 2 + 6 + 13)′ + или 3 + 5 = ∙ (2 + 6) +
Приравнивая коэффициенты при одинаковых степенях x , найдем = 32 и = −4, и можем брать интеграл:
|
|
(3x + 5) |
|
|
3 |
|
d(x2 + 6x + 13) |
|
|
|
|
d( + 3) |
||||||||||||
∫ |
|
|
|
= = |
|
|
|
|
∫ |
|
|
|
− 4 ∫ |
|
= |
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
√x2 + 6x + 13 |
√x2 + 6x + 13 |
|
|
|
√( + 3)2 + 4 |
|||||||||||||||||||
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
√ 2 |
+ 6x + 13 + |
ln | + 3 + √( + 3) |
2 |
+ 4| + C |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
2 |
x |
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Второй способ решения - это способ вычисления интеграла с помощью замены,
которая получается, если в знаменателе подынтегральной функции выделить полный квадрат. Замена приводит к распаду интеграла на два берущихся интеграла, константы при которых совпадают с коэффициентами при интегрировании первым способом. Исходный интеграл примет вид
|
|
|
|
+ |
|
|
= + |
|
|
|
|
|
( − ) + |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫ |
|
|
|
|
|
|
|
= | = − | = ∫ |
|
|
|
|
|
|
|
|
= |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
√ + + |
|
|
= |
√( − )2 + 2 ( − ) + |
|||||||||||||||||
= ∫ |
|
|
|
∙ |
+ ∫ |
|
− |
|
|
|
|
= |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
√ 2 + ( − 2 ) |
|
|
|
√ 2 + ( − 2 ) |
|
|
|
||||||||||||
= |
|
|
∙ ∫ |
|
2 |
|
|
+ ( − ) ∙ ∫ |
|
|
|
|
|
= |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
√ |
|
|
|
|
|
|
||||||||||||||
|
2 + ( − 2 ) |
√ 2 + ( − 2 ) |
|
|
||||||||||||||||||
= ∙ √ 2 + ( − 2 ) + ( − ) ∙ | + √ 2 + ( − 2 )| + =

10
= ∙ √ + + + ( − ) ∙ | + + √ + + | +
|
|
Вернемся к примеру: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Выделяем в знаменателе полный квадрат 2 + 6 + 13 = ( + 3)2 + 4. |
|||||||||||||||||||||||||||||||
|
|
Очевидно, что за новую переменную необходимо взять t=x+3, тогда получим |
|||||||||||||||||||||||||||||||
x=t-3 и dx=dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∫ |
|
3 + 5 |
|
= ∫ |
3( |
− 3) + 5 |
= ∫ |
3 − 4 |
= |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
√ 2 + 6 + 13 |
|
|
|
|
|
|
|
|
|
√ 2 + 4 |
√ 2 + 4 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= 3 |
∫ |
|
|
|
|
|
|
− 4 ∫ |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
√ 2 |
+ 4 |
|
|
|
|
|
|
|
√ 2 |
+ 4 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
√ |
2 |
+ 4 − |
∙ | + |
√ |
2 |
+ 4| + = |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
∙ 2 |
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∙ √ |
|
− |
4 |
∙ | + 3 + √ |
|
+ + |
||||||||||||||||||||||||||
= 3 |
2 + 6 + 13 |
2 + 6 + 13| |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для упорядочения данного материала ниже представлена таблица, которая помогает увидеть все методы вместе.
интегрирование рациональных дробей, у которых в знаменателе многочлен, имеющий отрицательный
дискриминант
вид интеграла |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
||||||||||||||||
(исходный) |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 + 2 + |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
√2 + 2 + |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
первый способ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подбор |
|
|
|
|
|
|
|
+ = ∙ ( 2 |
+ 2 + )′ + |
||||||||||||||||||||
коэффициентов и |
|
|
|
|
|
|
|
|
|
|
|
|
|
= /2 |
|||||||||||||||
по определенному |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= − ∙ |
||||||||||||||||
алгоритму |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ ∫ |
( 2 + 2 + ) |
|
|
|
|
∙ ∫ |
( 2 + 2 + ) |
|||||||||||||||||||
Сумма интегралов к |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
||||||||
|
|
2 |
+ 2 + |
|
√ |
|
|
|
|
||||||||||||||||||||
|
|
|
2 + 2 + |
||||||||||||||||||||||||||
которым сводится |
|
|
|
|
|
|
( + ) |
|
|
|
|
|
|
|
|
|
|
( + ) |
|||||||||||
исходный |
|
+ ∙ ∫ |
|
|
|
|
|
|
+ ∙ ∫ |
|
|
|
|
||||||||||||||||
|
( + )2 + ( − 2 ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
√( + )2 + ( − 2 ) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
∙ | 2 |
+ 2 + | + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Окончательный |
|
|
|
∙ 2 ∙ √ 2 + 2 + + |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
+ |
|
|
|
|
||||||||||||||||||
результат |
+ |
|
|
∙ ( |
|
|
) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
√ − 2 |
|
√ − 2 |
|
+ ∙ | + + √ 2 + 2 + | + |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
второй способ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
использование замены |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
