
2-й семестр / Лекция 14
.pdf



|
Пример 1. Вычислить |
поток |
|
|
|
|
|
F |
(x 2z)i |
(x 3y z) j |
(5x y)k |
векторного поля через треугольник ,
вырезанный из плоскости ( p) : x y z 1 0 координатными плоскостями, в том направлении нормали к плоскости, которая образует с осью Oz острый угол.
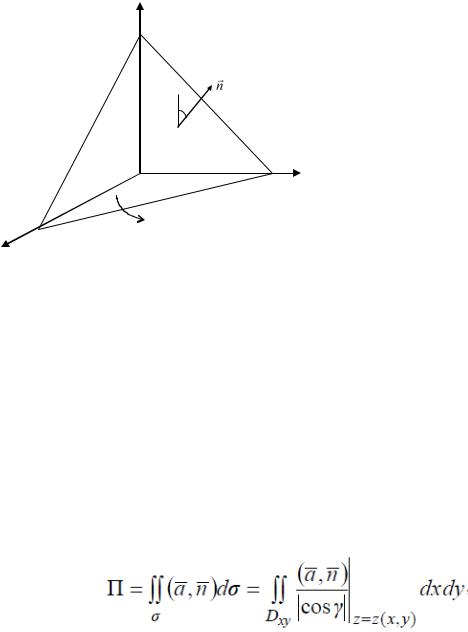
z
γ
O
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
Sxy |
|
|
|
|
|
|
|
|
|
x |
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
В |
данном |
примере поверхностью |
|
является |
|||||||
|
||||||||||||
треугольник ABC , лежащий в плоскости |
( p) |
: |
x y z 1 0 |
, отсюда |
||||||||
|
|
|
|
|
||||||||
z 1 x y |
|
поверхность проецируется |
|
взаимно |
однозначно на |
|||||||
|
. Эта |
|
||||||||||
плоскость |
xOy |
в область |
S |
xy – треугольник |
OAB |
(Рис.1). |
|
|||||
|
|
|||||||||||
|
|
|
|
|
|
|||||||
Следовательно, вычисление потока П через выбранную сторону
поверхности |
|
можно свести к вычислению двойного интеграла |
|
,
где – угол, который образует с осью Oz нормаль к поверхности .
|
|
|
|
|
|
|
|
|
Единичный вектор нормали n к выбранной стороне поверхности |
||||||||
найдем по формуле ̅ = ± |
|
= ± |
+̅̅+̅ |
, |
||||
| | |
|
|
|
|||||
|
|
|
|
|
√3 |
|||
где берется знак "+", если угол |
между осью Oz и нормалью острый, |
|||||||
и знак "–", если угол |
|
тупой. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
По условию задачи, нормаль к плоскости, в которой лежит треугольник ABC , образует острый угол с осью Oz , поэтому в формуле возьмем знак "+".

Следовательно,
cos
1 
 3
3
.
Найдем скалярное произведение
|
|
(x 2z) |
1 |
(x 3y z) |
1 |
(5x y) |
1 |
|
7 |
x |
4 |
y |
1 |
F |
n |
3 |
3 |
3 |
3 |
3 |
3 |
||||||
|
|
|
|
|
|
|
|
Применяя формулу, приведенную выше, вычислим искомый поток:
z
.
П |
|
|
|
|
|
|
7 |
|
4 |
|
1 |
|
|
|
|
|
|
|
|
F |
n d |
|
|
x |
|
y |
|
z |
3 |
dxdy |
(8x 5y 1)dxdy |
||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Sxy |
|
3 |
3 |
|
3 |
|
|
z 1 x y |
|
|
Sxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
1 x |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
(8x 5y 1)dxdy |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||




