Семинар 13

Добавил:

Rumpelstilzchen Rumpelstilzchen2018@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Линейная алгебра

Файл:

- не является матрицей Грама, так как на главной диагонали

- не является матрицей Грама, так как на главной диагонали

.pdf

Скачиваний:

Добавлен:

02.06.2020

Размер:

576.27 Кб

Скачать

☆

Семинар по теме

Евклидово пространство

Матрица Грама скалярного произведения

Определение 1. Будем говорить, что в действительном линейном пространст-

ве L определено скалярное произведение векторов, если

Каждой паре векторов x и y этого пространства поставим в соответствие ве-

щественное число, обозначаемое (x, y) так, что x, y, z L , R вы-

полняются следующие аксиомы (аксиомы скалярного произведения):

I. (x, y) = ( y, x)

II. (x y, z) = (x, z) ( y, z) III. ( x, y) (x, y)

IV. (x, x) 0 , причем (x, x) 0 x 0

Определение 2. Скалярное произведение (x, x) называется скалярным квад-

ратом вектора x и обозначается x2 : (x, x) x2

Свойства:

1R (x, y) (x, y) x, y L , R

2R (x, y z) (x, z) (x, z) x, y, z L , , , R

3R (0, y) (0 x, y) 0 (x, y) 0

Определение 3. Евклидовым пространством называется линейное веществен-

ное пространство, в котором задана операция скалярного ум-

ножения векторов.

Евклидово пространство принято обозначать E

Евклидово n-мерное пространство будем обозначать En .

МАТРИЦА ГРАМА В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ

Пусть En - n –мерное евклидово пространство и пусть e {e1,e2,...,en} - базис

в нем

					2
	(e , e )	(e , e ) ...		(e , e )		Матрица Г называется матрицей Грама
	(e , e )	(e , e ) ...		(e , e )		Матрица Г называется матрицей Грама
	1 1	1 2		1 n		скалярного произведения для базиса e .
	(e2 , e1)	(e2 , e2 ) ...		(e2 , en )		скалярного произведения для базиса e .
Г
	.	.	...	.
	.	.	...	.		Составлена из скалярных произведений
						Составлена из скалярных произведений
	(en , e1)	(en , e2 )
	(en , e1)	(en , e2 )	... (en , en )			всех пар базисных векторов
						всех пар базисных векторов

Формула для вычисления скалярного произведения векторов, заданных коорди-

натами в некотором базисе e в евклидовом пространстве En

(x, y) X T ГY

Свойства матрицы Грама

1Г Матрица Грама симметрична относительно главной диагонали.

2Г Элементы, стоящие на главной диагонали в матрице Грама строго поло-

жительны.

3Г Для матрицы Грама и для любого n-мерного столбца X выполняется условие

X T ГX 0 .

4Г . Определитель матрицы Грама в любом базисе положителен.

Пример 1. Могут ли быть матрицами Грама следующие матрицы:

1.1.			1	2	- не является матрицей Грама, так как матрица не симметрич-
1.1.	Г				- не является матрицей Грама, так как матрица не симметрич-
	1
			1	1
на и нарушается свойство 1Г .
1.2.	Г		1	2	- не является матрицей Грама, так как определитель матрицы
1.2.	Г	2			- не является матрицей Грама, так как определитель матрицы
		2
			2	1
меньше 0. Нарушается свойство 4Г .
1.3.	Г		1	1
1.3.	Г	3			- является матрицей Грама, так как выполняются все усло-
		3		2
			1	2

вия 1Г - 4Г (матрица симметрична, на главной диагонали расположены положительные значения, определитель матрицы больше 0).

не все элементы положительны. Нарушается свойство 2Г .

Задание 1. Выполнить самостоятельно

Могут ли быть матрицами Грама следующие матрицы? Указать, какое из

свойств нарушается.

	1		3	4		3		2	3

а) Г1		3	1 5		в) Г3		2 2		1
		4	5	2			4	1	2
		4	5	2			4	1	2

	4		2	7		8		3	1

б) Г2		2 1		1	г) Г4		3 2		0
		7	1	5			1	0	1
		7	1	5			1	0	1

Пример 2. В пространстве P2[t] многочленов степени не выше 2-х скалярное

произведение задано формулой ( f , g) f (t)g(t)dt . Составить матрицу Грама ска-

лярного произведения в каноническом базисе пространства {1,t,t 2} .

Решение.

	(e , e )		(e , e )		(e , e )
	1	1	1	2	1	3
Г	(e2 , e1) (e2 , e2 )				(e2 , e3 )
	(e3, e1) (e3, e2 )
	(e3, e1) (e3, e2 )				(e3, e3 )
Найдём все попарные произведения базисных элементов							e	1, e	t, e	t2 :
							1	2	3

1	1									1 1 2
(e1,e1) f (t)g(t)dt 1dt t


1	1
1		t	3				1		2
1			3				1
(e1, e3 ) (e3, e1) 1 t 2dt
(e1, e3 ) (e3, e1) 1 t 2dt
1	3						1		3
1							1
1	2dt			t		4		1
1						4		1
(e2 , e3 ) (e3, e2 ) t t									0
(e2 , e3 ) (e3, e2 ) t t									0
1					4			1
1					4			1
Матрица Грама будет иметь вид:
											2

								Г			0

											2	3
												3

					1							t			2	1
					1										2	1
		(e1, e2 ) (e2 , e1) 1 tdt														0
		(e1, e2 ) (e2 , e1) 1 tdt														0
					1								2			1
				1	1			1								1
						t	3				2
							3
		(e2 , e2 ) t tdt
		(e2 , e2 ) t tdt
				1	3			1			3
				1				1
				1			t		5	1				2
				1					5	1
		(e3, e3 ) t 2			t 2dt
		(e3, e3 ) t 2			t 2dt									5
				1				5		1				5
				1				5		1
0		2	3
			3
2	3	0		.
	3
0		2	5
			5

Задание 2. Выполнить самостоятельно.

В пространстве P2[t] многочленов степени не выше 2-х скалярное произведе-

ние задано формулой ( f , g) (1 t) f (t)g(t)dt . Составить матрицу Грама скалярно-

го произведения в каноническом базисе пространства {1,t,t 2} .

Задание 3. Выполнить самостоятельно. В евклидовом пространстве P2[t] из

примера 2, найти скалярное произведение многочленов f (t) 1 t	и g(t) 1 2t с
помощью матрицы Грама

ПРЕОБРАЗОВАНИЕ МАТРИЦЫ ГРАМА ПРИ СМЕНЕ БАЗИСА

	Пусть		e {e1,e2,..., en}, f { f1, f2,..., fn} -								два различных базиса в En .
	Пусть Гe , Г f		- матрицы Грама скалярного произведения в базисах e и f соответ-
	ственно. Пусть Ce f				-	матрица перехода от базиса e					к базису f . Связь между
	матрицами Грама в различных базисах пространства En задается формулой
							Г	f	CT	Г C
							Г		CT	Г C
									e f	e e f
	Задание 4. Выполнить самостоятельно.
	Задание 4. Выполнить самостоятельно.
	В базисе {e1,e2,e3} пространства E3 скалярное произведение задано матрицей
Грама Гe . Найти матрицу Грама Г f									скалярного произведения в базисе { f } , если
			1	2	4
							f1 e1 2e2 2e3 , f2 e1				e3 , f3 3e1 e2
	Г	2 5			3	,	f1 e1 2e2 2e3 , f2 e1				e3 , f3 3e1 e2
		1		3	3
		1		3	3

ДЛИНА ВЕКТОРА. УГОЛ МЕЖДУ ВЕКТОРАМИ

Определение 4. Длиной вектора (или модулем вектора) называется число, рав-

ное арифметическому значение квадратного корня из скалярного квадрата этого векто-

ра x 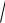(x, x) 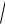x2

Свойства:

1. x 0 причем x 0 x 0

2.x x , R

3.Неравенство Коши-Буняковского. В любом евклидовом пространстве мо-

дуль скалярного произведения двух векторов не превосходит произведения их длин.

(x, y) x y

4. Неравенство треугольника x y x y

Определение 5. Углом между ненулевыми векторами x и y называется такое

действительное число , что														cos				(x, y)
																			x		y


Пример 3. Найти длины элементов																								f (t) 3t 2 ,								g(t) t 3 евклидова про-
									1																												1
									1				со скалярным произведением ( f , g)																									f (t)g(t)dt
странства всех многочленов P [t]													со скалярным произведением ( f , g)																									f (t)g(t)dt
																																					1
Решение. Чтобы найти длины элементов f и g, найдем скалярные квадраты
		1																	(3t 2)3							1		125			1
		1																	(3t 2)3							1		125			1
( f , f ) (3t 2)(3t 2)dt																																	14
( f , f ) (3t 2)(3t 2)dt																					9								9		9		14
				1																	9					1			9		9



	f	14
		1														(t 3)3						1					64		8	56
		1														(t 3)3						1					64		8	56
(g, g) (t 3)(t 3)dt
(g, g) (t 3)(t 3)dt																		3									3		3		3
				1														3					1				3		3		3



	g		56				2		14
			56				2		14

		3							3
		3							3
Нам понадобится
		1														1
	( f , g) (3t 2)(t												3)dt (3t 2 11t 6)dt
					1												1
				11t		2						1
						2						1
	t3							6t					14
	t3							6t					14
		2
		2										1
																																		( f , g)

Для нахождения угла													( f , g) , найдем cos ( f , g)
																																			f	g



cos ( f , g)									( f , g)							14									3
										f	g														2
																				56

															14
															14			3
																		3

Значит ( f , g)
Значит ( f , g)	6
	6
Задание 5. Выполнить самостоятельно. Найти длины элементов f (t) 1 t ,
g(t) 3 евклидова пространства всех многочленов		P [t]	со скалярным произведением
		1

( f , g) f (t)g(t)dt Найти угол между элементами.

1
Задание 6.	Выполнить самостоятельно. Найти длины элементов				f (t) 1 t ,
g(t) 1 t евклидова пространства всех многочленов P [t]			со скалярным произведением
		1
0
( f , g) (t 1) f (t)g(t)dt . Найти угол между элементами
1
Задание	7.	Выполнить самостоятельно.	Найти	длины	элементов
f (t) 1 2t , g(t) 1 t		евклидова пространства всех многочленов		P [t] со скалярным
				1

произведением ( f , g) f (t)g(t)dt . Найти угол между элементами

Пример 4. В базисе {e} пространства En скалярное произведение задано матрицей

Грама Г . Найти

1)Длины базисных векторов и угол между ними.

2)Длины векторов x и y и угол между ними

4.1. Пространство E		, базис {e , e } ,	2		1	,
	2		матрица Грама Г
		1 2		1	3

x e1 2e2 , y e1 e2

Решение 4.1.

1) Как известно, матрица Грама в данном базисе – матрица из попарных скаляр-

ных произведений базисных векторов:

		(e , e )			(e , e )												(e , e )					(e , e )						2 1
Г		1	1				1			2		.		Тогда				1		1		1 2					=	1 3
		(e , e )			(e , e )												(e , e ) (e , e )											1 3
		2 1					2 2											2 1				2 2
(e1, e1) 2				e1				(e1, e1) 2 ,

(e2 , e2 ) 3					e2				(e2 , e2 ) 3 ,
						(e , e )									1				1											1
cos (e , e )							1			2											(e , e					2	) arccos
							1			2

		1	2				e1			e2					2	3				6		1									6
							e1			e2					2	3				6											6
																	cos (x, y)						(x, y)
2)	x		(x, x) ,						y				( y, y) ,										(x, y)
2)	x		(x, x) ,						y				( y, y) ,
														2		1				1			x		y
(x, x) X T ГX																							x		y

					= (1																	=10		x				(x, x)	10
					= (1						2)											=10		x				(x, x)	10
														1		3
														1		3				2

( y, y) Y T ГY = (1	2		1	1
	2		1	1	=7	y	( y, y) 7
	-1)				=7	y	( y, y) 7
		1
		1	3	1

Для нахождения угла между векторами, найдем сначала скалярное произведе-

ние (x, y)

(x, y) X T ГY = (1			2			1		1	=-5
(x, y) X T ГY = (1			2)						=-5
				1		3
				1		3		1
		5			5
cos (x, y)		5			5		70		70
cos (x, y)
	10 7					70			14

				70
				70

(x, y) arccos
				14
				14
										8

4.2. Пространство E3 , базис {e1,e2,e3} , матрица Грама Г											3
											1
											1

x e1 2e2 e3, y 2e1 e3

Решение 4.2.

1) Составим матрицу Грама в базисе {e1,e2,e3} :

	(e , e )				(e , e )		(e , e )
		1		1	1	2	1	3
Г	(e2 , e1) (e2 , e2 )						(e2	, e3 ) .
	(e3, e1)				(e3, e2 )
	(e3, e1)				(e3, e2 )		(e3, e3 )
			(e , e ) (e , e )				(e , e )			8 3		1
Тогда				1 1		1 2		1	3
Тогда			(e2 , e1) (e2 , e2 )				(e2 , e3 )			=	3 2	0
			(e3, e1) (e3, e2 )								1 0	1
			(e3, e1) (e3, e2 )				(e3, e3 )				1 0	1

(e1, e1) 8 e1 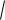(e1, e1) 22 , (e2 , e2 ) 2 e2 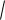(e2 , e2 ) 2 ,

					(e , e )							3										3
cos (e , e			)		1			2						(e , e )				arccos
					1			2

1		2			e				e			4				1	2				4
					e				e			4									4
					1				2

(e3, e3) 1				e3		(e3, e3) 1
					(e , e )
					(e , e )							1				2							2
cos (e , e )					1			3										(e , e ) arccos
cos (e , e )																		(e , e ) arccos
1		3			e				e			2			2	4		1	3				4
					e				e			2			2	4							4
					1				3
cos (e , e )					(e2 , e3 )								0	0 (e				, e )
cos (e , e )														0 (e				, e )
2		3			e2					e3		2					2	3	2
					e2					e3		2							2
																cos (x, y)			(x, y)
2)	x	(x, x) ,					y				( y, y) ,								(x, y)
																				x		y

3	1
2	0	,

0	1

		8		3	1	1
(x, x) X T ГX = (1		1)
(x, x) X T ГX = (1	2	1)	3	2	0	2	= 7	x		(x, x) 7

			1	0	1	1
			1	0	1	1
		8		3	1	2
( y, y) Y T ГY = (2	0 1)					0
( y, y) Y T ГY = (2	0 1)		3 2		0	0	= 29		y		( y, y) 29

			1	0	1	1

Для нахождения угла между векторами, найдем сначала скалярное произведе-

ние (x, y)
				8		3	1	2
(x, y) X T ГY = (1		2	1)		3	2	0	0	= 4

					1	0	1	1

cos (x, y)	4					4


	7	29			203
		4
(x, y) arccos
(x, y) arccos
		203

Задание 8. Выполнить самостоятельно. В базисе {e} пространства En скаляр-

ное произведение задано матрицей Грама Г . Найти

1)Длины базисных векторов и угол между ними.

2)Длины векторов x и y и угол между ними

8.1. Пространство E		, базис {e , e } ,		1		1
8.1. Пространство E	2	, базис {e , e } ,		матрица Грама Г			,
	2	1	2		1	2
					1	2
x 2e1 3e2 , y e1 e2
8.2. Пространство E		, базис {e , e } ,		4		3		,
8.2. Пространство E	2	, базис {e , e } ,		матрица Грама Г				,
	2	1	2		3	3
					3	3

x e1 e2 , y e1 2e2
	2		1	0
8.3. Пространство E3 , базис {e1,e2,e3} ,
8.3. Пространство E3 , базис {e1,e2,e3} ,	матрица Грама Г	1	2	3	,
		0	3
		0	3	8
x e1 e2 e3 , y 2e1 3e2 e3
	4		2	1
8.4. Пространство E3 , базис {e1,e2,e3} ,
8.4. Пространство E3 , базис {e1,e2,e3} ,	матрица Грама Г	2	3	0	,
		1	0	1
		1	0	1

x e1 e2 2e3 , y 2e12 e3

	9
Задание 9*.	Выполнить самостоятельно. В пространстве P2[t] много-
членов степени не	выше 2-х скалярное произведение задано формулой

( f , g) f ( 1)g( 1) f (0)g(0) f (1)g(1) . Показать евклидовость скалярного про-

изведения. Найти длины векторов f (t) 1 t t 2 , g(t) t и угол между ними. Со-

ставить матрицу Грама скалярного произведения в каноническом базисе пространства

{1,t,t 2} . Записать скалярное произведение в векторно-матричной форме

Ключевые вопросы лекции для подготовки к экзамену

1.Определение скалярного произведения векторов

2.Понятие квадратичной формы.

3.Матрица квадратичной формы

4. Изменение матрицы квадратичной формы при замене базиса.

5.Понятие конгруэнтных (эквивалентных) форм

6.Понятие ранга квадратичной формы.

7.Понятие вырожденной и невырожденной квадратичной формы

Соседние файлы в папке Семинары Пронина Е.В.

#
02.06.2020311.87 Кб21Семинар 08.pdf
#
02.06.2020732.96 Кб24Семинар 09.pdf
#
02.06.2020167.07 Кб16Семинар 10.pdf
#
02.06.2020307.63 Кб17Семинар 11.pdf
#
02.06.2020728.23 Кб17Семинар 12.pdf
#
02.06.2020576.27 Кб19Семинар 13.pdf
#
02.06.2020606.79 Кб16Семинар 14.pdf
#
02.06.2020498.24 Кб15Семинар 15.pdf
#
02.06.2020426.57 Кб15Семинар 16.pdf