
2-й семестр / Лекции Пронина Е.В. / Лекция 10
.pdf1
Канонический и нормальный вид квадратичной формы
Определение 1. Две квадратичные формы называются конгруэнтными (экви-
валентными), если существует невырожденное линейное преобразование, переводящее одну из них в другую.
Определение 2. Рангом квадратичной формы называется ранг матрицы этой формы в каком-либо базисе. Обозначается rf или r( f )
Определение 3. Квадратичная форма называется вырожденной, если ее ранг меньше размерности пространства Ln , и невырожденной, если ее ранг равен размерности пространства Ln .
n |
|
|
Определение 4. Квадратичная форма f (x) aij xi xj |
называется канониче- |
|
i, j 1 |
|
|
ской, если все коэффициенты aij 0 при i j . |
|
|
|
|
n |
То есть каноническая форма имеет вид: a11x12 a22 x22 |
... ann xn2 |
aii xi2 . |
i 1
Матрица такой формы является диагональной.
Определение 5. Каноническая форма называется нормальной, если каждый ее коэффициент, отличный от нуля (т.е. aii ) , по абсолютной ве-
личине равен 1.
Определение 6. Каноническим видом данной квадратичной формы называется конгруэнтная ей (эквивалентная) каноническая форма, т.е.
форма, не содержащая смешанных произведений неизвест-
ных.
Нахождение по данной квадратичной форме конгруэнтной ей канонической квадратичной формы называется приведением квадратичной формы к каноническому виду.
Определение 7. Базис, в котором квадратичная форма имеет канонический вид называют каноническим базисом.
Теорема 1. Основная теорема о квадратичных формах
Любая квадратичная форма, заданная в конечномерном пространст-
ве, с помощью невырожденного линейного преобразования коорди-
нат может быть приведена к каноническому виду
2
Теорема 2. Для любой вещественной квадратичной формы существует конгру-
энтная ей нормальная ей квадратичная форма.
Теорема 3. Ранг квадратичной формы сохраняется при любом невырожденном линейном преобразовании переменных.
n
Пусть квадратичная форма f (x) aij xi xj некоторым линейным преобразо-
i, j 1
n
ванием приведена к каноническому виду aii xi2
i 1
Теорема 4. Если квадратичная форма невырожденным линейным преобразова-
нием приведена к каноническому виду, то число отличных от нуля коэффициентов равно рангу r квадратичной формы.
В дальнейшем рассмотрим два способа приведения квадратичной формы к ка-
ноническому виду: метод Лагранжа и с помощью ортогонального преобразования.
Закон инерции квадратичных форм
Канонический вид, к которому приводится данная квадратичная форма, не явля-
ется для нее однозначно определенным: всякая квадратичная форма может быть при-
ведена к каноническому виду многими различными способами.
Тогда возникает вопрос, что общего у тех различных квадратичных форм, к ко-
торым приводится данная форма f? Этот вопрос связан с другим очень важным вопро-
сом: при каком условии одна из двух данных квадратичных форм может быть переве-
дена в другую невырожденным линейным преобразованием? Строго говоря, ответ на этот вопрос зависит от того, какие - комплексные или действительные - формы рас-
сматриваются.
Определение 8. Положительным индексом инерции квадратичной формы
называется число квадратов с положительными коэффициен-
тами в каноническом виде квадратичной формы. Обозначается
r ( f )
Определение 9. Отрицательным индексом инерции квадратичной формы
называется число квадратов с отрицательными коэффициен-
тами в каноническом виде квадратичной формы. Обозначается
r ( f )
3
Разность между положительным и отрицательным и отрицательным индексами инерции называется сигнатурой формы f.
Индексы инерции не зависят от способа приведения квадратичной формы к ка-
ноническому виду. Говорят, что ранг, индексы инерции и сигнатура формы инвари-
антны относительно преобразования координат.
Теорема 5. Закон инерции квадратичных форм: Все канонические формы,
конгруэнтные данной квадратичной форме имеют одинаковое число нулевых коэффициентов; одинаковое число положительных и отрицательных коэффициентов.
Индексы инерции связаны соотношением: r ( f ) + r ( f ) = r( f ) .
Теорема 6. Две квадратичные формы от n неизвестных с действительными ко-
эффициентами тогда и только тогда переводятся друг в друга не-
вырожденными действительными линейными преобразованиями,
если эти формы имеют одинаковые ранги и одинаковые сигнату-
ры.
Доказательство. Пусть форма f переводится в форму f’ невырожденным дейст-
вительным преобразованием. Как известно, такое преобразование не меняет ранга формы. Такое преобразование не может менять также и сигнатуры, так как тогда f и f’ приводились бы к различ-
ным нормальным видам. Но тогда форма f приводится к этим обо-
им нормальным видам, что противоречит закону инерции.
Обратно: если формы f и f’ имеют одинаковые ранги и одинако-
вые сигнатуры, то они приводятся к одному и тому же нормаль-
ному виду, а значит, могут быть переведены друг в друга.
МЕТОД ЛАГРАНЖА
ПРИВЕДЕНИЯ КВАДРАТИЧНОЙ ФОРМЫ
К КАНОНИЧЕСКОМУ ВИДУ
Обоснование метода основано на справедливости теоремы 1.
Для дальнейшего освоения метода нам понадобится повторить следующие важ-
ные формулы:
a2 2ab b2 (a b)2
a2 2ab b2 (a b)2
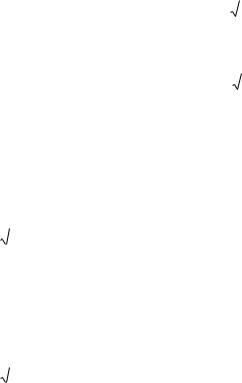
4
a2 b2 c2 2ab 2bc 2ac (a b c)2 a2 b2 c2 2ab 2bc 2ac (a b c)2 a2 b2 c2 2ab 2bc 2ac (a b c)2
Метод Лагранжа приведения квадратичной формы к каноническому виду осно-
ван на процедуре выделении полного квадрата. Рассмотрим метод выделения полного квадрата на примере функции двух переменных:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x2 |
4x x (2x )2 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. x |
2 |
4x x 6x |
2 |
|
(x 2x )2 |
2x |
2 |
(x 2x )2 |
( 2x)2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
1 |
|
2 |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
1 |
|
2 |
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x1 2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
|
|
|
|
|
(3x )2 6x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. x |
2 |
6x x 3x |
2 |
|
2 |
6x x |
2 |
(x 3x )2 |
6x2 |
(x 3x )2 ( 6x)2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
1 |
|
2 |
|
|
2 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
1 |
|
2 |
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x1 3x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||
3. |
x |
|
7x x |
2 |
3x |
2 |
|
|
7x x |
2 |
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
x |
2 |
|
|
3x |
2 |
x |
|
|
|
|
x |
2 |
|
|
|
|
|
|
x |
2 |
3x |
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
7 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
1 |
|
7 |
|
|
|
|
|
49 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
143 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
|
|
x |
2 |
|
|
|
|
|
x |
2 |
|
3x |
2 |
|
x |
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
7 |
|
|
|
49 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
7 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
2 |
|
|
|
|
4x |
|
2 |
x 4x |
|
2 16x2 x 4x |
|
2 |
|
|
4x |
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||
4. x |
2 |
8x x |
2 |
|
x2 |
8x x |
2 |
2 |
|
2 |
2 |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x1 4 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
143 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
|
|
x |
2 |
|
|
|
|
|
x |
2 |
|
3x |
2 |
|
x |
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
7 |
|
|
|
49 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
7 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Пример |
|
1. |
|
|
|
Привести |
|
|
к |
|
|
|
|
|
каноническому |
|
виду |
|
|
квадратичную |
|
|
|
|
форму |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q x2 |
|
2x2 |
7x2 |
2x x |
|
2x x |
4x x . |
|
|
|
Найти |
|
|
значение |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
2 |
|
|
|
1 |
3 |
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратичной формы на векторе a ( 1;5;0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сначала найдем матрицу квадратичной формы: Ae |
1 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Значение формы на векторе a может быть найдено по формуле:
5
1 1 |
1 |
1 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
f (x) ( 1,5,0) 1 |
2 |
2 |
|
5 |
|
(4,9,9) |
5 |
|
41 |
|
2 |
7 |
|
0 |
|
|
0 |
|
|
1 |
|
|
|
|
|
||||
Для приведения квадратичной формы к каноническому виду сгруппируем все слагаемые, содержащие неизвестное x1 , и дополним их до полного квадрата. Слагае-
мые, подчеркнутые одной чертой необходимы нам для соблюдения формулы, но, по-
скольку ранее их не было, то, добавив несуществующее ранее слагаемое, мы должны его же и вычесть (подчеркнуто двумя черточками):
Q(x , x , x ) (x2 |
2x x 2x x ) 2x2 |
7x2 |
4x x |
|
|
|
|
||||||||||||||||||||||
|
1 |
2 |
3 |
1 |
|
|
|
1 |
2 |
|
1 |
3 |
|
|
2 |
|
|
3 |
|
2 |
3 |
|
|
|
|
||||
(x2 |
x2 |
x2 |
x2 |
x2 |
2x x 2x x 2x x 2x x ) 2x2 |
7x2 |
4x x |
||||||||||||||||||||||
1 |
|
2 |
2 |
3 |
|
3 |
|
|
1 |
2 |
|
|
1 |
3 |
|
2 |
3 |
|
2 |
3 |
|
2 |
3 |
2 |
3 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 |
x2 |
x2 |
2x x 2x x 2x x ) x2 |
x2 |
2x x 2x2 |
7x2 |
4x x |
||||||||||||||||||||||
1 |
|
2 |
3 |
|
|
1 |
2 |
|
1 |
3 |
|
|
2 |
3 |
|
2 |
|
3 |
2 |
3 |
2 |
3 |
2 |
3 |
|||||
Приведем подобные слагаемые за скобкой и свернем скобку в полный квадрат:
Q(x1, x2 , x3 ) ... (x1 x2 x3 )2 x22 6x32 2x2 x3 .
!!! Обратите внимание: за скобкой нет слагаемых, содержащих неизвестное x1
Полный квадрат, содержащий неизвестное x1 , не изменяется. Среди оставшихся членов сгруппируем те, которые содержат неизвестное x2 , и дополним их до полного квадрата:
Q(x , x , x ) (x x x )2 |
x2 |
6x2 |
2x x (x x x )2 (x2 |
2x x x2 ) 5x2 |
|
|||||||||||||||||||||
|
1 |
2 |
3 |
|
1 |
2 |
3 |
2 |
|
3 |
2 |
3 |
1 |
2 |
3 |
|
2 |
|
|
2 |
3 |
3 |
3 |
|
||
(x x x )2 (x x )2 |
5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
2 |
|
3 |
|
2 |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перейдем от неизвестных x1 , |
x2 , |
x3 к неизвестным y1 , |
y2 , y3 |
по формулам: |
|
|
|
|
|
|||||||||||||||||
|
|
y |
x |
x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
x2 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда получим канонический вид квадратичной формы: Q y2 |
y2 |
5y2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
3 |
|
|
|
|
|
Напомним, что преобразование координат выглядит: |
X СY или Y С 1X |
|
|
|
|
|||||||||||||||||||||
Выполненное |
преобразование |
|
координат |
тогда |
можно |
переписать |
|
в |
виде: |
|
||||||||||||||||
y |
|
1 |
|
1 1 x |
|
x |
|
1 |
1 |
0 y |
|
|
|
|
1 |
1 |
0 |
|
||||||||
1 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
0 |
|
1 |
1 x2 |
или |
x2 |
|
|
0 |
1 |
1 y2 |
, где Ce f |
|
|
0 |
1 |
|
1 |
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
|
0 0 |
|
1 |
|
|
||
y3 |
|
|
|
0 1 x3 |
|
x3 |
|
|
1 y3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
C |
e f |
1 |
|
|
|
|
|
|
Ce f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Матрица формы в старом базисе e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
равна Ae 1 |
|
2 |
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрица формы в каноническом базисе: Af |
|
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сделаем проверку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
0 0 1 1 |
1 1 |
1 |
0 |
|
1 1 |
1 1 |
1 |
0 |
|
1 |
0 0 |
|||||||||||
A |
f |
CT |
A C |
|
1 |
1 0 |
1 2 |
2 |
|
0 |
1 1 |
|
|
0 1 1 |
|
0 1 |
1 |
|
|
0 |
1 0 |
|
|||||
|
e f |
e e f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
1 1 |
7 |
0 0 |
|
1 |
|
0 0 5 |
0 0 |
|
0 |
0 5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как число слагаемых в каноническом виде равно трем, то ранг формы равен трем.
Так как канонический вид квадратичной формы содержит три слагаемых с положи-
тельными коэффициентами, то положительный индекс инерции равен трем: r ( f ) 3
z |
x |
x |
|
x |
||
1 |
1 |
|
2 |
3 |
||
Если взять z2 |
|
x2 x3 , то получим нормальный вид квадратичной формы: |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
z3 |
|
|
|
5x3 |
||
Q z2 z2 z2 |
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
Пример 2. |
Привести |
|
к |
каноническому |
|
виду |
|
квадратичную форму |
|||||
f x2 |
8x2 |
4x2 |
4x x 4x x |
12x x . Записать соответствующее преобразо- |
|||||||||
1 |
2 |
3 |
1 |
2 |
1 |
3 |
2 |
3 |
|
|
|
|
|
вание координат. Определить ранг и индексы инерции формы. |
|
|
|||||||||||
Определить, какая поверхность определяется уравнением |
f (x) 1 |
||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выпишем матрицу квадратичной формы: Ae |
2 |
8 |
6 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
6 |
6 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сгруппируем все слагаемые, содержащие неизвестное |
x1 , и дополним их до |
||||||||||||
полного квадрата. |
|
|
|
|
|
|
|
|
|
|
|
||
Q (x12 4x1x2 4x1x3 ) 8x22 4x32 12x2 x3

7
(x2 |
4x2 |
4x2 |
4x |
2 |
4x2 |
4x x |
2 |
4x x 8x x 8x x ) |
|||||||||||||
1 |
2 |
|
2 |
|
3 |
3 |
1 |
1 |
3 |
2 |
3 |
2 |
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x2 |
4x2 |
12x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
3 |
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x12 4x22 4x32 4x1x2 4x1x3 8x2 x3 ) 4x22 4x32 8x2 x3 8x22 4x32 12x2 x3
Приведем подобные слагаемые за скобкой и свернем скобку в полный квадрат:
Q(x1 2x2 2x3 )2 4x22 4x2 x3 .
!!!Обратите внимание: за скобкой нет слагаемых, содержащих неизвестное x1
Полный квадрат, содержащий неизвестное x1 , не изменяется. Среди оставшихся членов сгруппируем те, которые содержат неизвестное x2 , и дополним их до полного квадрата:
Q (x1 2x2 2x3 )2 (4x22 4x2 x3 x32 ) x32
(x1 2x2 2x3 )2 (2x2 x3 )2 x32
|
|
Перейдем от неизвестных x1 , |
x2 , x3 |
к неизвестным y1 , |
y2 , y3 |
по формулам: |
|||||||||||||||||||||||||
|
|
y |
x |
2x |
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y2 |
|
|
|
2x2 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда получим канонический вид квадратичной формы: |
Q y2 |
y2 |
y2 . Заметим, что |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
форма приведена к нормальному виду. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Выполненное |
|
|
преобразование |
|
координат |
|
можно |
переписать в виде: |
|||||||||||||||||||||||
y |
|
1 2 |
2 x |
|
x |
|
1 |
1 |
1 y |
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|||
y2 |
|
|
0 |
|
|
2 |
1 |
x2 |
|
или x2 |
|
|
0 |
2 |
2 |
y2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 0 |
1 |
|
0 0 |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
y3 |
|
|
x3 |
|
x3 |
|
|
|
y3 |
|
|
|
|
|
|
|
|
||||||||||||||
x1 y1 y2 y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 |
|
|
|
|
y2 |
|
|
|
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|||
Матрица преобразования: Сe f |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напомним, матрица формы в старом базисе равна Ae |
|
2 |
8 |
6 |
|
, |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрица формы в каноническом базисе: Af |
|
0 |
1 |
0 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сделаем проверку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
2 2 1 |
1 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||
|
|
CT |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
A |
f |
A C |
e f |
|
1 |
|
|
0 |
|
2 |
8 6 |
|
0 |
1 |
|
|
|
||||||||
|
e f |
e |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
2 |
6 4 |
0 0 |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
2 1 |
1 |
1 |
|
1 0 |
0 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2 |
1 |
|
0 |
2 |
2 |
|
|
0 1 |
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 0 1 |
0 0 |
1 |
|
|
0 0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как число слагаемых в каноническом виде равно трем, то ранг равен трем.
Так как канонический вид квадратичной формы содержит два слагаемых с положи-
тельными коэффициентами и одно слагаемое с отрицательным коэффициентом, то по-
ложительный индекс инерции равен трем: r ( f ) 2 , а отрицательный индекс инерции r ( f ) 1. Сигнатура равна r ( f ) r ( f ) 1
Теперь посмотрим, какую поверхность IIго рода определяет уравнение
f (x) 1
Для удобства переобозначим координаты на привычные для геометрического представления:
y1 Xy2 Yy3 Z
|
|
Тогда уравнение примет вид |
X 2 Y 2 Z 2 1 - это уравнение определяет в |
||||||||
пространстве однополостный гиперболоид. |
|
||||||||||
|
|
Вопрос: Какая поверхность определялась уравнением из примера 1? |
|||||||||
|
|
Пример |
3. |
Исследовать |
тип |
поверхности, заданной уравнением |
|||||
4x2 |
|
3 |
x2 2 x2 2x x |
|
8x x 4x x |
1 в зависимости от параметра . |
|||||
4 |
|
||||||||||
1 |
|
2 |
3 |
1 |
2 |
1 |
3 |
2 |
3 |
|
|
Решение.
Приведем квадратичную форму к каноническому виду методом Лагранжа.
Сгруппируем все слагаемые, содержащие неизвестное x1 , и дополним их до полного квадрата.

9
4(x2 |
|
|
1 |
x x 2x x ) |
|
3 |
x2 |
2 x2 |
4x x |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
2 |
1 |
2 |
|
1 |
3 |
|
|
|
4 |
|
2 |
|
3 |
2 |
3 |
|
|
|
|
|
|
|
||||||
4(x2 |
|
|
1 |
x x |
|
1 |
x2 |
|
|
1 |
|
x2 |
2x x x2 |
x2 |
|
1 |
x x |
1 |
x x ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
2 |
1 |
2 |
|
16 |
|
2 |
16 |
2 |
1 |
3 |
3 |
|
3 |
|
2 |
2 |
3 |
2 |
2 |
3 |
||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x2 |
2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4 |
|
2 |
|
|
|
3 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4(x |
|
1 |
x |
x )2 |
2x x 4x2 |
|
1 |
x2 |
|
|
3 |
x2 |
2 x2 |
4x x |
||||
|
|
|
||||||||||||||||
1 |
4 |
2 |
3 |
2 |
3 |
3 |
|
4 |
|
2 |
|
4 |
2 |
3 |
2 |
3 |
||
4(x |
|
1 |
x |
x )2 |
4x2 |
x2 |
2 x2 |
2x x |
|
|
||||||||
|
|
|
||||||||||||||||
1 |
4 |
2 |
3 |
3 |
2 |
|
|
3 |
|
|
|
2 |
3 |
|
|
|
||
4(x1 14 x2 x3 )2 (x22 2x2 x3 x32 ) 3x32 2 x32
4(x1 14 x2 x3 )2 (x2 x3 )2 (2 3)x32
Перейдем от неизвестных x1 , x2 , x3 к неизвестным X , Y , Z по формулам:
X x |
|
1 |
x |
|
x |
|
|
|
2 |
|
|||||
|
1 |
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x3 |
|
|||
Y |
|
|
|
|
|||
Z |
|
|
|
|
|
x |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Тогда получим канонический вид квадратичной формы: 4X 2 Y 2 (2 3)Z 2 |
1 . |
||||||
Заметим, что канонический вид зависит от способа приведения квадратичной формы к такому виду. Неизменными остаются характеристики квадратичной формы, а именно ранг – количество квадратов в каноническом виде, положительный индекс инерции – количество квадратов с плюсом, и отрицательный индекс инерции – количество квадратов с минусом.
Продолжим исследование типа поверхности в зависимости от характеристик формы.
1. Если (2 3) 0 , то обозначим (2 3) с2 и уравнение поверхности примет
вид
4X 2 Y 2 с2Z 2 1
это уравнение задаёт в пространстве двуполостный гиперболоид. 2. Если (2 3) 0 , то уравнение примет вид
4 X 2 Y 2 1
ибудет определять цилиндрическую поверхность (гиперболическую)
3.Если (2 3) 0 , то обозначим (2 3) с2 и уравнение поверхности примет
вид
4X 2 Y 2 с2Z 2 1
это уравнение задаёт в пространстве однополостный гиперболоид.

10
Задача полностью решена.
Пример 4. Привести к каноническому виду квадратичную форму
f 4x1x2 5x2 x3
Решение. Для того чтобы выделить полный квадрат, нужно чтобы квадрат пе-
ременной входил с ненулевым коэффициентом. Поэтому, когда в форме отсутствуют квадраты неизвестных, сначала выполним невырожденное линейное преобразование
x1 y1 y2 |
|
1 |
1 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
y1 |
y2 |
с матрицей С1 |
1 |
1 |
|
: |
|
||
x2 |
0 |
X C1Y , откуда Y C1 |
X |
||||||
|
|
y3 |
|
|
0 |
1 |
|
|
|
x3 |
|
0 |
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
f 4( y y |
2 |
)( y y |
2 |
) 5( y y |
2 |
) y 4 y2 |
4 y2 |
5y y 5y |
2 |
y |
||||||
1 |
|
|
1 |
|
|
1 |
3 |
1 |
2 |
1 |
3 |
3 |
||||
Заметим, что матрица новой формы |
|
|
|
|
|
|
||||||||||
|
|
4 |
|
0 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
B |
|
0 |
|
4 |
5 |
|
|
|
|
|
|
|
|
|
||
|
|
5 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
2 |
5 |
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь коэффициент при y1 |
отличен от нуля, и поэтому из нашей формы можно |
||||||||||||||||||||||||||||||||||||||||||||
выделить квадрат неизвестного |
|
y1 . |
Сгруппируем все слагаемые, |
содержащие неиз- |
|||||||||||||||||||||||||||||||||||||||||||
вестное y1 , и дополним их до полного квадрата: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
f 4 y2 |
|
4 y2 |
5y y 5y |
2 |
y |
(4 y2 |
5y y ) 5y |
2 |
y 4 y2 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
1 |
3 |
|
3 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
25 |
|
|
|
|
2 |
|
|
|
|
|
|
25 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
4 y2 |
2 |
|
|
|
|
|
y y |
|
|
|
|
y |
|
|
4 |
|
|
|
|
y |
5y |
y 4 y2 |
|
|
|
||||||||||||||||||||||
|
2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
1 3 |
|
|
64 |
|
|
3 |
|
|
|
|
|
|
64 3 |
|
|
|
2 3 |
2 |
|
|
|
||||||||||||||||
|
|
5 |
|
|
|
|
2 |
|
25 |
|
y2 |
|
|
|
|
|
|
|
y 4 y2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4 y |
|
|
|
|
|
y |
|
|
|
|
5y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1 |
|
8 |
|
|
3 |
|
|
16 |
|
|
3 |
|
|
|
|
|
|
|
2 |
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
25 |
|
2 |
|
|
|
|
|
|
|
|||||
|
4 y |
|
|
|
|
y |
|
|
4 y |
|
2 |
|
|
|
|
|
|
|
y |
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
1 |
|
|
|
8 |
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
2 |
4 |
2 |
|
3 |
|
|
64 |
|
3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
2 |
|
|
|
|
|
|
5 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4 y |
|
|
|
|
|
y |
|
|
4 y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
|
8 |
|
|
|
3 |
|
|
|
|
|
2 |
|
8 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Перейдем от неизвестных y1 , |
y2 , |
|
y3 |
|
к неизвестным z1 , |
z2 , z3 |
по формулам: |
||||||||||||||||||||||||||||||||||||||
