
2-й семестр / Лекции Пронина Е.В. / Лекция 12
.pdf
1
Евклидово пространство.
Матрица Грама скалярного произведения
Понятие n-мерного линейного пространства не в полной мере обобщает понятия плоскости или трехмерного евклидова пространства в n-мерном случае. Так, в частно-
сти, в n - мерном случае при n > 3 не определены ни длина вектора, ни угол между век-
торами. В связи с этим, становится невозможным развитие той богатой геометрической теории, знакомой нам для двух- и трехмерного пространства. Однако, эту ситуацию можно изменить.
Как известно из курса аналитической геометрии, на плоскости и в пространстве можно ввести понятие скалярного произведения векторов. Оно определяется с исполь-
зованием длин векторов и угла между ними. С другой стороны, мы знаем, что и угол между векторами, и длина вектора могут быть выражены через скалярное произведе-
ние. В связи с этим, имеет смысл определить скалярное произведение в любом n-
мерном линейном пространстве аксиоматически, с использованием некоторых свойств, которыми обладает скалярное умножение векторов на плоскости и в трехмер-
ном пространстве.
Рассмотрим линейное вещественное (или комплексное) пространство L . Наря-
ду с имеющимися в нем операциями сложения векторов и умножения вектора на число
(действительное или комплексное) введем еще одну внутреннюю алгебраическую опе-
рацию, являющуюся обобщением скалярного произведения геометрических векторов.
В основу определения этой операции положим свойства скалярного произведения гео-
метрических векторов, полученные в аналитической геометрии ранее.
Определения скалярного произведения в случае, когда L рассматривается над полем действительных чисел или над полем комплексных чисел отличаются друг от друга.
Определение 1. Будем говорить, что в действительном линейном пространст-
ве L определено скалярное произведение векторов, если
Каждой паре векторов x и y этого пространства поставим в соответствие ве-
щественное число, обозначаемое (x, y) так, что x, y, z L , R выполняются следующие аксиомы (аксиомы скалярного произведения):
I. (x, y) = ( y, x)
II. (x y, z) = (x, z) ( y, z)

2
III. ( x, y) (x, y)
IV. (x, x) 0 , причем (x, x) 0 x 0
Определение 2. Скалярное произведение (x, x) называется скалярным квад-
ратом вектора x и обозначается x2 : (x, x) x2
Укажем несколько важных свойств скалярного произведения векторов в веще-
ственном линейном пространстве, вытекающие из аксиом:
1R (x, y) (x, y) x, y L , R
2R (x, y z) (x, z) (x, z) x, y, z L , , , R 3R (0, y) (0 x, y) 0 (x, y) 0
Определение 3. Будем говорить, что в комплексном линейном пространстве L
определено скалярное произведение векторов, если
Каждой паре векторов x и y этого пространства поставим в соответствие
комплексное число, обозначаемое (x, y) так, что x, y, z L , С выполняются следующие аксиомы (аксиомы скалярного произведения):
I. (x, y) = ( y, x)
II. (x y, z) = (x, z) ( y, z)
III. ( x, y) (x, y)
IV. (x, x) 0 , причем (x, x) 0 x 0
Свойства скалярного произведения векторов в комплексном линейном про-
странстве:
1С (x, y) (x, y) x, y L , С
2С (x, y z) (x, z) (x, z) x, y, z L , , , С 3С (0, y) (0 x, y) 0 (x, y) 0
Докажем свойство 1С для скалярного произведения векторов в комплексном
1 |
|
|
III |
|
|
|
|
|
1 |
|
|
линейном пространстве (x, y) ( y, x) |
|
( y, x) ( y, x) (x, y) |
|||||||||
Задание* Установить чему равны скалярные произведения, рассмотренные ни-
же. Обосновать вывод, пользуясь аксиомами для соответствующего линейного про-
странства.

3
4R ( x y, z) , x, y, z L , , , R 4С ( x y, z) , x, y, z L , , , С
Пространство над полем R |
Пространство над полем С |
|
|
Аксиомы |
Аксиомы |
I. (x, y) = ( y, x) |
|
|
|
|
|
||
I. (x, y) = ( y, x) |
|||||||
II. (x y, z) = (x, z) ( y, z) |
II. (x y, z) = (x, z) ( y, z) |
||||||
III. ( x, y) (x, y) |
III. ( x, y) (x, y) |
||||||
IV. (x, x) 0 , (x, x) 0 x 0 |
IV. (x, x) 0 , (x, x) 0 x 0 |
||||||
|
|
||||||
Свойства |
Свойства |
||||||
x, y, z L , , , R |
x, y, z L , , , С |
||||||
1R (x, y) (x, y) |
|
|
|
|
|
||
1 |
|
(x, y) (x, y) |
|||||
2R (x, y z) (x, z) (x, z) |
С |
|
|
|
|
|
|
2 |
С |
(x, y z) (x, z) (x, z) |
|||||
3R (0, y) (0 x, y) 0 (x, y) 0 |
|
|
|
|
|
|
|
3С (0, y) (0 x, y) 0 (x, y) 0 |
|||||||
4R ( x y, z) |
4С ( x y, z) |
||||||
|
|||||||
Определение 4. Евклидовым пространством называется линейное веществен-
ное пространство, в котором задана операция скалярного ум-
ножения векторов.
Евклидово пространство принято обозначать E
Определение 5. Унитарным пространством называется комплексное линейное пространство, в котором определено скалярное произведение векторов.
Унитарное пространство принято обозначать U .
В частности n-мерное линейное пространство, в котором введено скалярное произведение векторов, называется n-мерным евклидовым (или унитарным) про-
странством. Евклидово n-мерное пространство будем обозначать En (унитарное про-
странство - Un ).
Так как и евклидово, и унитарное пространства являются линейными простран-
ствами, то для них верно всё то, что было сказано об этих пространствах ранее. Но введение скалярного произведения позволяет ввести в этих пространствах метрику.
4
Теорема 1. При любом n в n-мерном линейном пространстве можно определить скалярное умножение, т.е. можно превратить его в евклидово про-
странство.
ПРИМЕРЫ ЕВКЛИДОВЫХ ПРОСТРАНСТВ
Пример 1. Пусть C[a,b] – множество всех непрерывных на промежутке
[a,b] действительных функций. Как рассматривалось ранее, это множество является
линейным пространством. Определим скалярное произведение следующим образом.
Если f (x) и g(x) |
– две непрерывные на [a,b] функции, |
то пусть |
|
|
|
( f , g) f (x)g(x)dx . |
Из свойств определённого интеграла следует, что все требо- |
|
|
|
|
вания определения 1 выполняются. Следовательно, если в пространстве |
всех непре- |
|
рывных на промежутке [a,b] действительных функций ввести указанным способом скалярное произведение, то оно становится евклидовым пространством.
Пример 2. Пусть M 2 2[R] – множество квадратных матриц с действительны-
ми элементами. Как было показано ранее, оно является линейным пространством на
полем |
|
|
R . |
|
Определим |
|
скалярное |
произведение |
формулой |
|||||
|
|
|
|
|
|
|
|
|
|
. Легко проверить, что все требования опреде- |
||||
|
|
|
|
1 |
1 |
|
1 |
|||||||
|
|
|
|
1 |
1 |
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ления 1 выполняются. Множество M 2 2[R] стало евклидовым пространством.
Пример 3. Пусть M 2 2[C] – множество квадратных матриц с комплексными элементами. Это множество является линейным пространством на полем C . Опреде-
лим |
скалярное |
произведение |
формулой |
|
|
|
|
|
||
( A, B) |
|
|
1 |
1 |
|
|||||
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
. Легко проверит, что все требования опреде- |
|||||||||||||
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|||||||||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ления 3 выполняются. Получили пример унитарного пространства.
5
Пример 4. В n -мерном пространстве арифметических векторов Rn можно вве-
|
|
x |
|
|
y |
|
|
|
|
1 |
|
|
1 |
|
|
сти скалярное |
умножением, сопоставив элементам |
X ... |
|
, |
Y ... |
|
число |
|
|
|
|
|
|
|
|
|
|
xn |
|
|
yn |
|
|
X TY x y ... x y . |
|
|
|
|
|
|
|
1 1 |
n n |
|
|
|
|
|
|
Пример 5. Пусть Pn[t] – множество всех многочленов с действительными ко-
эффициентами степени не выше n. Как рассматривалось ранее, это множество является линейным пространством. Определим скалярное произведение следующим образом.
Если |
p(x) p |
0 |
p x ... p |
n |
x n |
и q(x) |
q |
0 |
q |
x ...q |
n |
xn – два многочлена из |
|
|
1 |
|
|
|
1 |
|
|
||||
Pn[t] , то ( p, q) p0 q0 p1q1 ...pn qn . |
Следовательно, |
если в пространстве Pn[t] |
||||||||||
всех многочленов с действительными коэффициентами степени не выше n ввести ука-
занным способом скалярное произведение, то оно становится евклидовым пространст-
вом.
Далее речь пойдет о евклидовых пространствах.
Из рассмотренных примеров видно, что в n-мерном линейном пространстве ска-
лярное умножением можно задать по-разному, превратив его в n-мерное евклидово пространство, что определяется выбором базиса.
МАТРИЦА ГРАМА В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Пусть En - n –мерное евклидово пространство и пусть e {e1,e2,...,en} - базис
в нем. Так как в En для любой упорядоченной пары векторов определено их скаляр-
ное произведение, то определены скалярные произведения всех пар базисных векто-
ров. Составим из них матрицу
|
(e , e ) |
(e , e ) ... |
(e , e ) |
|||||
|
1 |
1 |
1 |
|
2 |
1 |
n |
|
|
(e2 |
, e1) |
(e2 |
, e2 ) ... |
(e2 |
, en ) |
||
Г |
|
|
|
|
|
|
|
|
|
|
. |
|
. |
... |
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
(en , e1) |
(en , e2 ) ... |
|
|
|
|||
|
(en , en ) |
|||||||
6
Матрица Г называется матрицей Грама скалярного произведения для базиса e
. Используя матрицу Грама можно получить формулу для вычисления скалярного про-
изведения векторов, заданных координатами в некотором базисе e .
Пусть {e1,e2 ,..., en}- базис в En . Пусть {x1, x2 ,..., xn}, {y1, y2 ,..., yn} - коорди-
наты векторов x и y в этом базисе. Это означает, что имеет место следующее пред-
ставление векторов в разложении по базису:
x x1e1 x2e2 ... xnen , y y1e1 y2e2 ... ynen
Тогда
(x, y) (x1e1 x2e2 ... xnen ) ( y1e1 y2e2 ... ynen )
|
n |
|
xi y j (ei , e j ) X T ГY , где X T - строка координат вектора X, Y – столбец коорди- |
i, j 1
нат вектора Y.
(x, y) X T ГY
Свойства матрицы Грама
1Г Матрица Грама симметрична относительно главной диагонали.
Действительно, это следует из того, что (ei , e j ) (e j , ei ) .
2Г Элементы, стоящие на главной диагонали в матрице Грама строго поло-
жительны.
Действительно, так как каждый базисный вектор ei 0 , а на главной диагонали
стоят элементы (ei , ei ) ei2 0 .
3Г Для матрицы Грама и для любого n-мерного столбца X выполняется условие
X T ГX 0 .
Это также следует непосредственно из аксиомы IV скалярного произведения.
Определение 6. Симметрическую матрицу A, удовлетворяющую условию
X T ГX 0 для любого ненулевого столбца X называют по-
ложительно определенной.
Значит, мы можем сказать, что матрица Грама положительно определена.
4Г . Определитель матрицы Грама в любом базисе положителен.
7
Можно сказать, что скалярное произведение является симметрической били-
нейной формой. Причем, соответствующая ей квадратичная форма - положительно оп-
ределенная.
Пример 6. Могут ли быть матрицами Грама следующие матрицы:
|
|
|
6.1. |
Г |
1 |
2 |
|
|
|
6.2. |
Г |
|
|
|
1 |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
6.3. |
Г |
|
|
|
1 |
1 |
|
|
6.4. |
Г |
|
|
|
2 |
1 |
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
6.1. |
Г |
1 |
2 |
- не является матрицей Грама, так как матрица не симметрич- |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на и нарушается свойство 1Г . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
6.2. |
Г |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как определитель матрицы |
||||||
|
|
|
2 |
|
- не является матрицей Грама, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
меньше 0. Нарушается свойство 4Г . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
6.3. |
Г |
|
|
1 |
1 |
- является матрицей Грама, так как выполняются все усло- |
||||||||||||||||||||
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вия 1Г - 4Г (матрица симметрична, на главной диагонали расположены положительные |
|||||||||||||||||||||||||||||
значения, определитель матрицы больше 0). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Проверка условия 3Г : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Г |
|
x x |
|
1 |
1 x |
|
(x x |
|
|
|
|
|
|
|
x |
|
|
|
|
2x )x |
|||||||||
|
|
|
|
|
1 |
|
x 2x ) |
1 |
(x x )x ( x |
||||||||||||||||||||
|
3 |
|
1 |
|
2 1 2 |
x |
|
|
1 |
2 |
|
|
1 |
|
|
2 |
x |
2 |
|
1 |
2 1 |
1 |
2 2 |
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 |
x x |
2 |
x x 2x2 |
|
x2 |
2x x |
2 |
x2 x2 |
(x x )2 |
x2 |
|
|
|
||||||||||||||||
|
|
1 |
1 |
|
|
1 |
2 |
2 |
|
1 |
1 |
|
|
2 |
|
|
2 |
|
1 |
|
2 |
2 |
|
|
|
||||
|
|
|
6.4. |
Г |
|
|
2 |
1 |
- не является матрицей Грама, так как на главной диагонали |
||||||||||||||||||||
|
|
|
4 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не все элементы положительны. Нарушается свойство 2Г . |
|
|
|
||||||||||||||||||||||||||
|
|
|
Пример 7. В базисе {e} пространства En скалярное произведение задано матрицей |
||||||||||||||||||||||||||
Грама Г . Найти скалярное произведение векторов x и y. |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
7.1. Пространство E |
|
, базис {e , e } |
, |
матрица Грама |
4 |
2 |
|
|||||||||||||||||||
|
|
|
2 |
Г |
|
, x = (–3, 1) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
и y = (2, –7).

8
Решение 7.1. Используя формулу (1), получим
(x, y) X T ГY =
7.2. Пространство E3 , базис {e1,e2,
x = (1, –5, 4) и y= (–3, 2, 7).
( 3 |
4 |
2 |
|
2 |
=1 |
|
|
|
|
|
1) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
4 |
|
|
|
e3} , матрица Грама |
|
|
|
|
|
|
||||
Г |
1 |
2 |
0 |
|
, |
|||||
|
|
|
|
|
|
4 |
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|||
Решение 7.2. Используя формулу (1), получим |
|
|
|
|
|
|
|
|
||
|
6 |
1 |
4 |
|
|
3 |
|
|
||
(x, y) X T ГY = (1 |
- 5 4) |
1 |
2 |
0 |
|
|
|
2 |
|
= 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
3 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
||||
Пример 8. В пространстве P2[t] |
многочленов степени не выше 2-х скалярное |
|||||||||
1
произведение задано формулой ( p, q) p(t)q(t)dt . Составить матрицу Грама этого
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скалярного произведения в каноническом базисе пространства {1,t,t 2} . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(e , e ) |
(e , e ) |
|
(e , e ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Г |
|
1 |
1 |
|
1 |
|
2 |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
(e2 , e1) |
(e2 , e2 ) (e2 , e3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(e3, e1) |
(e3, e2 ) (e3, e3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Найдём все попарные произведения базисных элементов |
e |
1, e |
|
|
t, e |
t2 : |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 tdt |
t 2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(e1 , e1 ) 1 1dt t |
|
2 |
|
|
|
|
|
(e , e ) (e |
|
, e ) |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
2 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
t |
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
3 |
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(e1, e3 ) (e3, e1) 1 t 2dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
(e2 , e2 ) t tdt |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
3 |
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
1 |
3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
t |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
t |
5 |
|
1 |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(e2 , e3 ) (e3, e2 ) t t |
2dt |
|
|
|
|
|
0 |
|
|
|
|
|
(e3, e3 ) t 2 |
t 2dt |
|
|
|
|
|
|||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||||||||||||||||||||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5 |
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Матрица Грама будет иметь вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
0 |
2 |
3 |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
0 |
|
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

9
ПРЕОБРАЗОВАНИЕ МАТРИЦЫ ГРАМА ПРИ СМЕНЕ БАЗИСА
Пусть e {e1,e2,..., en}, f { f1, f2,..., fn} - два различных базиса в En .
Пусть Гe , Г f - матрицы Грама скалярного произведения в базисах e и f соответ-
ственно. Пусть Ce f - матрица перехода от базиса e к базису f . Тогда в базисе
e скалярное произведение запишется в виде:
T |
(1) |
(x, y) X e |
ГeYe |
Преобразование координат каждого вектора выглядит следующим образом:
Xe Ce f X f Ye Ce f Yf |
|
|
(2) |
Подставим формулы (2) в (1) |
|
|
|
T |
T |
T |
(3) |
(x, y) Ce f X f Гe Ce f Yf X f |
Ce f ГeCe f Yf |
|
|
В базисе f скалярное произведение запишется в виде: |
|
||
T |
Г f Yf |
(4) |
|
(x, y) X f |
|
||
Сравнивая скалярные произведения в правых частях равенств (3) и (4), получим связь между матрицами Грама в различных базисах пространства En :
X Tf Г f Yf X Tf CeT f ГeCe f Yf
|
|
|
|
|
CT |
|
|
|
|
(5) |
|
|
|
|
Г |
f |
|
Г C |
|
|
|
|
|
||
|
|
|
|
e f |
e e f |
|
|
|
|
|
||
Пример 9. В базисе {e} пространства En скалярное произведение задано матрицей |
||||||||||||
Грама Гe . Найти матрицу Грама Г f |
|
скалярного произведения в базисе { f } . |
|
|
|
|||||||
9.1. Пространство E |
|
, |
|
базис |
|
{e , e } , |
матрица |
Грама |
4 |
2 |
, |
|
2 |
|
|
Г |
|
||||||||
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
f1 2e1 e2 , f2 e1 e2 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
Решение 9.1. |
|
|
|
|
|
|
|
|
|
|
|
|
Матрица перехода: C |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
e f |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
Используя формулу (5), получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
Г |
|
CT |
Г C |
2 |
1 T |
4 2 2 |
1 |
10 7 |
2 |
1 |
27 |
|
17 |
||||||||
f |
= |
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|||||
|
e f |
e e f |
|
|
2 3 |
|
|
|
|
5 |
|
1 |
|
|
|
|
11 |
|
|||
|
|
|
|
1 |
1 |
1 |
1 |
6 |
|
1 |
17 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
4 |
|
|
|
|
9.2. Пространство E3 , базис {e1,e2,e3} , матрица Грама |
|
|
|
|
|
|
|
|
|||||||||||||
Г |
1 |
2 |
0 |
|
, |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f1 e1 e2 e3 , |
f2 e1 2e3 , |
f3 2e1 e2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение 9.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрица перехода: Ce f |
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя формулу (5), получим |
|
|
|
|
|
|
|
|
|
|||||
|
1 1 |
2 T 6 |
1 4 1 1 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г f |
CeT f ГeCe f = |
1 |
0 |
1 |
|
|
1 |
2 |
0 |
|
1 |
0 |
1 |
|
|
|
1 |
2 |
0 |
|
|
4 |
0 |
3 |
|
1 |
2 |
0 |
|
|
|
|
|
|
|
|||||||||
3 |
3 |
1 1 1 |
2 |
5 5 |
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
14 |
1 |
10 |
1 |
0 |
1 |
|
= |
3 |
34 |
27 |
|
|
0 8 |
|
1 |
2 |
0 |
|
|
3 |
27 |
|
|
11 |
|
|
|
22 |
|||||||
ВВЕДЕНИЕ МЕТРИКИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Пусть En – n-мерное евклидово пространство.
Определение 7. Длиной вектора (или модулем вектора) называется число, рав-
ное арифметическому значение квадратного корня из скаляр-
ного квадрата этого вектора x 
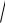 (x, x)
(x, x) 
 x2
x2
Свойства:
1.x 0 причем x 0 x 0
2.x x , R
3.Неравенство Коши-Буняковского. В любом евклидовом пространстве мо-
дуль скалярного произведения двух векторов не превосходит произведения их длин.
(x, y) x y
