Часть 2. Изучение влияния запаздывания.

Передаточная функция разомкнутой системы с запаздыванием может быть записана так:

W(p) = W_ (p) W₁(p) ,

где: W₁(p) – передаточная функция системы без учета запа-здывания,

W_ (p )– передаточная функция звена запаздывания

W_ (p) = e^{  p}.

Структурно система с запаздыванием может быть представлена следующим образом:

Работа производится со схемой варианта А. Предварительно вычисляется для этой системы K_гр и устанавливается коэффициент усиления разомкнутой системы K = ( 0,4 – 0,45 ) K_кр. Берут начальное значение ₀ равным 0 (система без запаздывания) и получают на экране монитора АФХ системы с нанесенной разметкой частот. Затем получают еще 2 – 3 АФХ системы при различных значениях времени запаздывания  с той же разметкой частот (рекомендуется взять шаг  = (0,15 – 0,2) T₁).

Полученные кривые АФХ системы без запаздывания и с различными значениями времени запаздывания нужно перенести на миллиметровку на один график (масштаб по осям абсцисс и ординат должен быть одинаков!) и с помощью циркуля показать, что при изменении  модуль W(j) не меняется, а меняется только фаза.

Определение критического времени запаздывания

Нужно определить критическое время запаздывания _кр при выбранном в части 2 коэффициенте усиления. При этом используется кривая АФХ системы без запаздывания. Для точного определения _кр рекомендуется эксперимен-тально определить значение частоты _к , при которой W(j_к)  1, и определяется угол  между вещественной отрицательной полуосью и вектором W(j_к) для вычисления _кр:

Обращаем внимание, что величина угла должна быть выражена в радианах.

Отчет по лабораторной работе должен содержать:

• наименование и цель работы;

• структурные схемы и исходные данные;

• выражения, по которым строятся АФХ для структурных схем вариантов А и Б;

• графики АФХ, полученные в первой части, с соответствующими выводами и вычисленные значения K_кр ;

• семейство характеристик АФХ при различных значениях  с разметкой частот и пояснения, как влияет запаздывание на вид АФХ;

• график, поясняющий определение критического времени запаздывания и его вычисленное значение;

• запасы по фазе и амплитуде, определенные по кривой АФХ системы без запаздывания, полученной во второй части работы.

Контрольные вопросы для зачета

1. Укажите отличия статической и астатической систем.

2. Приведите формулировку критерия Найквиста для статических и астатических систем.

3. Как определяется критическое время запаздывания?

4. Как влияет запаздывание на вид АФХ?

5. Приведите формулы для определения запаса устойчи -вости по фазе.

6. Приведите формулы для определения запаса устойчи-вости по амплитуде.

7. Какие критерии устойчивости Вы ещё знаете?

8. На каком принципе основан критерий устойчивости

Михайлова?

9. Дайте формулировку критерия Гурвица.

10. Приведите сравнение критериев устойчивости.

Лабораторная работа 6 Оценка качества регулирования сар

Цель работы: 1) Изучение показателей качества линейных систем автоматического регулирования.

2). Изучение влияния параметров САУ на показатели качества.

Постановка задачи: В данной лабораторной работе изучаются прямые и косвенные оценки качества линейных систем, наиболее часто применяемые при анализе и синтезе систем, и влияние на них одного из параметров - коэффициента усиления системы.

Прямые оценки качества определяют по кривой переходной характеристики х_вых(t) = h (t), получаемой при воздействии единичной ступенчатой функции х_вх (t) = 1(t) при нулевых начальных условиях. Если САУ описывается линейным дифференциальным уравнением с постоянными коэффициентами, то при подаче на вход воздействия x_вх (t), выходную величину x_вых(t) можно записать так:

x_св(t) + x_в x_вых(t) = (t) ,

где x_вых(t) – решение дифференциального уравнения, описывающего систему; x_св(t) – свободная составляющая переходного процесса, соответствующая решению однородного дифференциального уравнения; x_в(t) –вынуж-денная (установившаяся) составляющая, по которой определяют точность системы.

Точность системы при подаче на вход единичного ступенчатого воздействия – статическая ошибка  определяется как разность между заданным х_з и установившимся h_уст значениями выходной величины и выражается в процентах от заданного значения:

Прямые оценки качества, характеризующие переходный процесс, которые рассматриваются в данной работе:

1. Перерегулирование  – максимальное отклонение переходной характеристики от установившегося значения выходной величины, выраженное в относительных единицах или процентах:

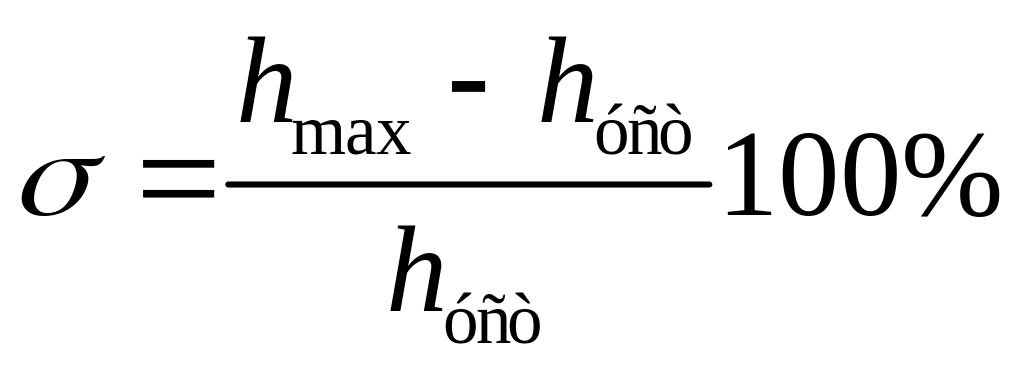
где h_max – значение первого максимума переходной характеристики.

2. Время регулирования t_p – минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью:

 h(t)  h_уст    при t  t_p ,

где  – постоянная величина, задаваемая в процентах от установившегося значения выходной величины h_уст . Обычно принимают  = 0,05 h_уст .

Косвенные оценки качества системы, рассматриваемые в данной работе.

1. Показатель колебательности системы M – определяется по амплитудной частотной характеристике замкнутой системы как отношение максимального значения АЧХ A_max () к ее значению при  = 0

M = A_max () / A (0)

Для астатических систем А (0) = 1 и М = А_max .

2. Корневые методы оценки качества регулирования – определяются по расположению корней характеристического уравнения замкнутой системы на комплексной плоскости:

а) Степень устойчивости  – расстояние от мнимой оси до ближайшего корня или ближайшей пары сопряженных комп-лексных корней.

б) Колебательность системы  – максимальное отношение мнимой части корня _i к действительной части _i,

 = tg  = ( _i /  _i ) _max

Другими словами колебательность системы  определяет тангенс угла, образованного отрицательной вещественной полуосью и лучом из начала координат к корню, у которого отношение мнимой части к действительной максимально.

В данной работе исследуется система автоматического регулирования, имеющая структурную схему:

Постоянные времени Т₁ , Т₂ и Т₃ , (T₁  T₂  T₃) задаются преподавателем.