20. Гиперкубы
Гиперкубом
(n-мерный
куб) Hn
называется граф, каждая вершина которого
взаимнооднозначно соответствуют
области пространства и 2 вершины
соединены ребром, если они соответствуют
соседним областям.
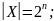
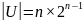
Свойства:
h(Hn) = 2 (2 цвета вершин)
Гиперкуб используется для вложения в производные графов с целью определения характеристик последних.
H(Hn) = n (цвет ребер)
Максимальная длина цепи: lmax = 2n-1; d(Hn) = n;
Запрещенными фигурами для вписания графа в гиперкуб являются графы с циклами нечетной длины и К23.
Граф называется вложенным в булевое пространство или кубируемым, если существует взаимнооднознозначное соответствие между вершинами графа и гиперкубом. Граф, который не вписывается в гиперкуб – некубируемый.
Число цепей, которое соединяет 2 произвольные вершины гиперкуба равняется n!
21. Логика высказываний. Логические функции от двух переменных.
Высказыванием будем называть повествовательное предложение, о котором можно сказать в данный момент времени истинно оно или ложно. (1-истина. 0 – ложь).
Все преобразования над сложными высказываниями происходят по законам мат. Логики.
Если имеется n переменных, т.е. имеются переменные Х1, Х2,…Хn. То из них можно построить логическую функцию различными способами.
Форма, в которой функция представлена в виде дизъюнкции всех конституент, называется совершенной нормальной дизъюнктивной формой (сднф).
Существует 16 различных логических функций от двух переменных.
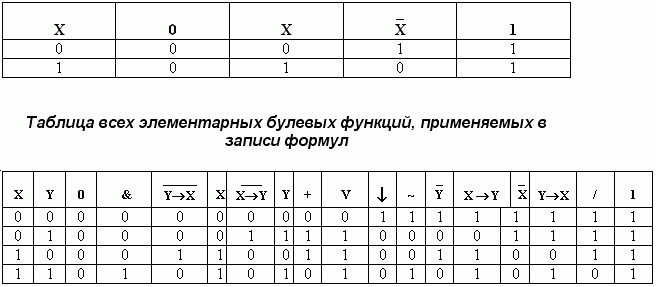
22. Минимизация булевых функций в классе днф.
Основным методом минимизации логических функций, представленных в виде ДНФ и КНФ, является операция попарного неполного склеивания и элементарного поглощения.
Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые или инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшееся в скобках прямое и инверсное вхождение переменной подвергнуть склейке.
Таким образом, главной задачей при минимизации является поиск термов (членов), пригодных к склейке с последующим поглощением. Карты Карно и метод Квайна предоставляют наглядный способ отыскания таких термов.
Импликантой булевой функции f называют всякую булевую функцию g, обращение которой в 1 возможно лишь на тех наборах переменных, на которых на которых обращается в 1 функция f
Конъюнкция соответствующая max единичному интервалу f, называется простой импликантой этой функции, а дизъюнкция всех простых импликант наз-ся сокращенно ДНФ.
Процедура минимизации булевой функции заключается в попарном сравнении конституент соседних ярусов.