15. Планарные и плоские графы.

Граф G=(X, U) называется плоским, если его ребра, расположенные на плоскости, могут иметь общие точки только в инцидентных им вершинах, т.е. не пересекаются (рис. 9.1).

Граф, изоморфный плоскому и расположенный на плоскости с пересечением ребер, называется планарным (рис. 9.2).

Область плоскости, ограниченная ребрами плоского графа, внутри которой нет ни вершин, ни ребер, называют гранью. Ребра грани образуют простой цикл. Заметим, что плоский граф имеет всегда одну бесконечную грань, не ограниченную ребрами (f₆ на рис. 9.1).

Существует формула Эйлера, позволяющая установить связь между числом вершин n, ребер m и граней f плоского графа:

n – m + f = 2.

Теорема Понтрягина – Куратовского. Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных полному графу K₅ и полному двудольному графу K_3,3 (рис. 9.3,а,б).

Основываясь на критерии Понтрягина, можно получить еще один критерий планарности, введя понятие элементарного стягивания, состоящего в следующем. При стягивании любого ребра графа оно исключается, а обе вершины a и b, инцидентные ему, отождествляются (рис. 9.3,а,б). Полученная при этом вершина инцидентна тем же ребрам, что и a, b (кроме исключенного ребра).

Теорема Харари. Граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых к K₅ и K_3,3.

Теорема Харари является двойственной формой теоремы Понтрягина-Куратовского.

Минимальное число ребер, которое нужно удалить из графа, чтобы он стал планарным, называется числом планарности и обозначается (G).

Для полного графа K_n c n  4 вершин (G) определяется как

.

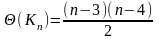16. Эйлеров путь в графе.

Маршрут (u₁, u₂,..., u_q) называется циклом, если в нем начальная вершина дуги u₁ совпадает с конечной вершиной дуги u_q.

Так, например, в графе, приведенном на рис. 3.1, последовательности дуг:

₁={u₁, u₅, u₂}, ₂={u₁, u₅, u₂, u₃, u₁₀, u₄}, ₃={u₁, u₅, u₈, u₁₀, u₄},

₄ ={u₁, u₅, u₈, u₁₀, u₄, u₂, u₉, u₇, u₆, u₃} – являются циклами.

Цикл называется эйлеровым, если он содержит все ребра графа ровно один раз.

Теорема (Эйлера). Граф содержит эйлеров цикл только тогда, когда все его вершины имеют четную степень.

Например, граф, изображенный на рис. 3.1, будет содержать Эйлеров цикл (₄), а граф, изображенный на рис. 3.2, – нет.

Цикл называется простым, если каждая вершина, принадлежащая циклу, используется только один раз (за исключением начальной и конечной вершин, которые совпадают).

Например, пути ₁ и ₃ являются простыми циклами, а путь ₂ не является простым циклом, так как вершина x₁ используется в нем дважды.

Простой цикл, проходящий через все вершины графа, имеет особое значение и называется гамильтоновым циклом. Конечно, не все графы обладают гамильтоновыми циклами. Так, например, путь ₃ является гамильтоновым циклом графа, приведенного на рис. 3.1, а граф на рис. 3.2 не имеет гамильтонова цикла. В отличие от эйлерового цикла для гамильтонова цикла неизвестен простой критерий его существования в произвольном графе.

Контуром называется цикл в ориентированном графе. Таким образом, контур является путем (x₁, x₂,..., x_q), в котором совпадают начальная и конечная вершины, т. е. в котором x₁ = x_q.

На рис. 3.3 маршруты

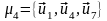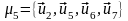, и

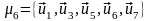
являются контурами.

Цикломатическим числом графа (G) называется число независимых простых циклов, содержащихся в графе. Оно вычисляется по формуле:

(G) = m – n + 1. (3.1)

Например, количество независимых контуров электрической цепи определяется цикломатическим числом.