13. Операции над графами.

1) Дополнение графа G = (x, U).

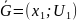
Это граф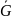 , у которого носитель совпадает с исходным графом и множество дуг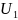 есть дополнение для множества дуг U.

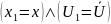
2) Объединение графов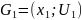

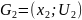
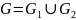
При условии, что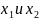 не пересекаются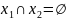

G = (x, U) у которого множество вершин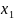 объединены с 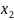и дуги образованы с .

3) Сумма графов

Граф G = (x, U) образован путем объединения графов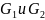 и построения полного двудольного графа, у которого одна доля представляет собой множество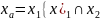 , а 2 доля

4) Удаление вершины x из графа G = (x, U)

5) Удаление ребра из графа

14. Устойчивость, покрытия, паросочетания в графе.

ОПР. Инвариантом графа G называется число, связанное с этим графом, которое принимает одно и то же значение на любом графе, изоморфном данному.

Вершина накрывает ребро , если это ребро инцидентно данной вершине.

Ребро, концидентное покрывает вершину. Каждое ребро и каждая вершина покрывают сами себя.

2 инварианта:

1) min число вершин (ребер) которые показывают все ребра (вершины).

2) наибольшее число несмежных ребер и наибольшее число несмежных вершин.

ОПР. Множество вершин, показывающих все ребра графа называют вершинным покрытием графа, а множество ребер, показывающих все вершины называют реберным покрытием графа.

ОПР. Множество вершин называется внутренне устойчивым, если они попарно не смежны.

ОПР. Внутренне устойчивое множество вершин называется пустым подграфом, если при добавлении хотя бы одной вершины, не принадлежащей этому множеству образуется хотя бы 1 ребро.

Характеристики:

ОПР. Max мощность пустого подграфа называется числом внутренней устойчивости или вершинным числом независимости.

ОПР. Мах число попарно несмежных ребер называется реберным числом независимости графа.

ОПР. Min мощность вершинного покрытия называется числом вершинного покрытия графа.

ОПР. Min мощность реберного покрытия графа называется числом реберного покрытия и обозначается .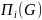

ОПР. Min мощность множества вершин, показывающих все вершины графа называется вершинным числом внешней устойчивости графа и обозначается .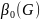

ОПР. Реберное число внешней устойчивости – min мощность множества ребер, показывающих все ребра графа.

ТЕОРЕМА: для любого нетривиального графа G = (x, G) справедливо следующее

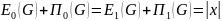4 + 6 = 5 + 5 = 10

ОПР. Множество ребер графа, в котором никакая пара ребер несмежна называется паросочетанием графа, а множество ребер паросочетаний, в которых число ребер равняется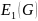 называется наибольшим паросочетанем графа. a, m, 0

Теорема Кёнига: для двудольного графа G число ребер в наибольшем паросочетании равно числу вершинного покрытия. .

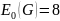15. Продолжение.

Толщиной графа G называется наименьшее число планарных графов, в результате объединения которых получается исходный граф G. Толщина планарного графа равна 1.

Нижняя оценка толщины t(G) определяется неравенством

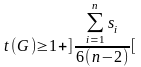, (9.3)

где 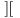– большее целое число, |X| = n, S_i – степень i-й вершины.