33. Структурное проектирование автоматов с минимальным объемом внутренней памяти.
Исходной информацией для проектирования являются результаты построения автоматного оператора, а результатом должна быть логическая схема устройства. Результатом структурного проектирования является построение принципиальной электрической схемы.
Любое состояние автомата фиксируется набором состояний запоминающих элементов, входящих во внутреннюю память автомата и число таких элементов соответствует разрядности кодирования.
Алгоритм:
Выбрать число элементов памяти:
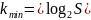
Где S – количество состояний, скобки обозначают округление до ближайшего целого
Закодировать все состояния
Получить канонические уравнения всех видов запоминающих элементов и выходов автомата. Для чего формируется таблица переходов и выходов. Каноническое уравнение показывает условия, при которых элементы памяти переходят в противоположное состояние.
Построить логическую схему устройства
При выборе минимального числа элементов памяти требуется меньшее число элементов памяти, но при этом получается довольно сложная входная логика.
34. Структурное проектирование автоматов с максимальным объемом внутренней памяти
Исходной информацией для проектирования являются результаты построения автоматного оператора, а результатом должна быть логическая схема устройства. Результатом структурного проектирования является построение принципиальной электрической схемы.
Любое состояние автомата фиксируется набором состояний запоминающих элементов, входящих во внутреннюю память автомата и число таких элементов соответствует разрядности кодирования.
Алгоритм:
Выбрать число элементов памяти:
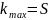
Где S – количество состояний
Закодировать все состояния. Используется унитарное кодирование, то есть в каждом коде присутствует ровно 1 единица.
Получить канонические уравнения всех видов запоминающих элементов и выходов автомата. Для чего формируется таблица переходов и выходов. Каноническое уравнение показывает условия, при которых элементы памяти переходят в противоположное состояние.
Построить логическую схему устройства
При проектировании автомата с применением max объема внутренней памяти увеличивается стоимость памяти(число элементов), но упрощается входная логика.
(1) Способы задания графов.
(2) Маршруты, цепи, циклы.
(3) Кратчайшие пути в графах. Алгоритм Дейкстры.
(4) М. Форда-Беллмана реш. зад о кратчай пути.
(5) Матем. постан задачи Коммивояжера.
(6) М. ветвей и границ реш. задачи коммивояжера.
(7) Матем. постановка транспортной задачи.
(8) Распределительный метод.
(9) Модифицир. распред. м. транспортной задачи.
(10) Цикломатическое число графа.
(11) Деревья. Остовное дерево минимального.
(12) Тополог. сортировка Алгоритм Демукрона
(13) Операции над графами.
(14) Устойчивость, покрытия, паросочет. в графе.
(15) Планарные и плоские графы.
(16) Эйлеров путь в графе.
(17) Потоки в сетях. Теор. Форда-Фалкерсона.
(18) Связность графов. Теорема Менгера.
(19) Раскраска вершин и ребер графа.
(20) Гиперкубы.
(21) Лог. высказ. Лог. фун. от двух переменных.
(22) Минимиз. булевых функций в классе ДНФ.
(23) Минимиз. бул. фун. с помощью карты карно.
(24) Метод Квайна-Мак-Класки.
(25) Полнота логических функций.
(26) Минимиз слабоопред булевых фун.
(27) Схемы из функциональных элементов.
(28) Синтез лог. схем в произвольном базисе.
(29) Разлож Шеннона. Дифферен. булевых фун.
(30) Матем. модели цифровых устр-в. с памятью.
(31) Алгоритмический этап проект-я ц.автомата.
(32) Абстрактное проект-ие автоматов.
(33) Структурное проектирование автоматов с минимальным объемом внутренней памяти.
(34) Структурное проектирование автоматов с максимальным объемом внутренней памяти.