1. Способы задания графов

1) Геометрический (графический)

Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.

2) Теоретико-множественный

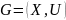
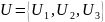
3)Матричный

а) Матрица инцидентности

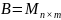n-число вершин, m – число дуг или ребер

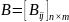
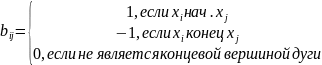
Для неорграфа:

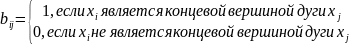
б) Матрица смежности

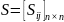
Неорграф:

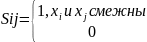
Орграф:

2. Маршруты, цепи, циклы

Маршрутом в графе называется {x₁,r₁,x₂,r₂,…x_n}

чередующиеся последовательность вершин и ребер/дуг.

Неорграф:

Цепью ρ=(r_1, … r_n) называется упорядоченная последовательность ребер в которой у каждого ребра r_i одна из граничных вершин является граничной вершиной r_i-1, а другие r_i+1. Если вершины и ребра в цепи различны, то маршрут называют простой цепью. Замкнутая цепь называется циклом, а замкнутая простая цепь называется простым циклом.

Орграф:

Путем в графе называется упорядоченная последовательность дуг μ = (U_1, …, U_n), в которой конец предыдущей дуги совпадает с началом последующей. Путь у которого начальные и конечные вершины совпадают – контур. Длина цепи – число ребер в цепи. Граф называется связным, если любая пара его вершин соединены цепью. Минимальная длина цепи, соединяющая вершины x_i и x_j называется расстоянием. Максимальное расстояние между вершинами графа называется диаметром графа. . Цепь (неорграф) называют составной, если в ней повторяется хотя бы одно ребро; сложной, если повторяется хотя бы одна вершина. Простой цикл называется гамильтоновым, если он проходит через каждую вершину графа ровно 1 раз. В орграфе путь, проходящий через все вершины ровно 1 раз, называется гамильтоновым, если у него начальная и конечная вершина совпадают, то гамильтонов контур.

3. Алгоритм Дейкстры.

Пусть l(x_i) – пометка вершины x_i.

Шаг 1. Присвоение начальных значений. Положить l*(s)=0 и считать эту пометку постоянной. Положить l(x_i)=∞ (бесконечность) для всех x_is и считать эти пометки временными. Положить р=s.

Шаг 2. Обновление пометок. Для всех вершин x_iГ(р), имеющих временные пометки, изменить пометки в соответствии с выражением:

l(x_i) = min{l(x_i), l(p) + c(p, x_i)}. (2.3)

Шаг 3. Превращение пометки в постоянную. Среди всех вершин с временными пометками найти такую, для которой l*(x_i) = min{l(x_i)}.

Шаг 4. Считать пометку вершины x_i* постоянной и положить p = x_i*.

Шаг 5. Если р=t, то l*(р) является длиной кратчайшего пути. Конец. Если рt, перейти к шагу 2.

Как только длина кратчайшего пути от s до t будет найдена [она будет постоянной пометкой вершины l*(t)], сами пути можно получить с помощью рекурсивной процедуры. Так, для вершины x_k, непосредственно предшествующей вершине t в кратчайшем пути от s к t, будет соблюдаться отношение: l*(x_k) + c(x_k, t) = l*(t).

Таким образом, для любой вершины x_i можно найти предшествующую вершину x_k, принадлежащую пути (s, t), для которой справедливо:

l*(x_k) + c(x_k, x_i) = l*(x_i). (2.4)

Если существуют несколько кратчайших путей от s к t, то данное соотношение будет выполняться для нескольких вершин. В этом случае выбор пути может быть произвольным.

4. Метод Форда-Беллмана решения задачи о кратчайшем пути в графе.

Алгоритм Ф.Б. позволяет находить кратчайшие пути от источника S до любой вершины, при этом веса дуг могут быть как “+”, так и “-“.

Исходные данные: граф C помечен дугами, а результат помечен вершинами.

1) Присвоение начального значения меток

Установить номер итерации k=0, присвоить начальное значение меток следующим образом:

2) Обновление пометки вершин

Для каждой вершины Xj =Г(S) установить пометку следующим образом:

Где Tj = Г^-1 множество вершины, которые входят в Xj и связан с вершиной X

3) Проверка условий окончания

Если k <= n-1 и П^к+1 (Xj) != П^к (Xj) хотя бы для 1 вершины, то переход к шагу 4 если

П^к+1 (Xj) = П^к (Xj), то конец алгоритма.

4) Подготовка к следующей итерации

Определить множество S, как множество таких X, что

Пометки П (Xi) у всех вершин графа характеризуют расстояние от источника Х1 до данной вершины.

5. Математическая постановка задачи коммивояжера

Задача коммивояжера имеет следующую формулировку. Имеется n городов, расстояния между которыми известны. Коммивояжер должен посетить все n городов по одному разу, вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным.

Сформулируем математическую модель задачи коммивояжера. Пусть имеется n городов и задана матрица С = ||c_ij||_nn расстояний между городами. Очевидно, что с_ii = 0, и, возможно, что с_ij  c_ji.

Введем переменные

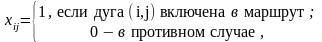
где i, j = 1,2,…, n.

Задача поиска гамильтонова контура минимальной длины сводится к определению таких x_ij , обеспечивающих минимум целевой функции

(3.2)

при следующих ограничениях:

(3.3)

и

. (3.4)

Ограничения (3.3) обеспечивают требования въезда в каждый j-й город ровно 1 раз (вхождения в j-ю вершину графа ровно одной дуги). Ограничения (3.4) обеспечивают требования выезда из каждого i-го города ровно 1 раз (выхода из i-й вершины графа ровно одной дуги). Задача представляет собой задачу дискретного программирования с псевдобулевыми переменными.