1.Мех.движ. Сист.отсчёта. Кинематика мат.точки. Путь и перемещение. Траектория движения Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени.

Система отсчета.

Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой.

Итак, элементами системы отсчета, необходимыми для описания движений, являются: начало отсчета, масштабы отсчета расстояний, три направления отсчета положения тел, начало отсчета времени, масштаб времени.

Для определения положения материальной точки в любой момент времени необходимо также задать начало отсчета времени.

Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела.

Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно.

Путь и перемещение.

Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путем. Вектор, соединяющий начальную и конечную точки траектории, называется перемещением.

Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение .

Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением

Поступательное и вращательное движения — самые простые примеры механического, движения тел.

2.Поступательное и вращательное движение. Скорость и ускорение при поступательном и вращательном движении. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, перемещается параллельно сама себе.(кабина лифта). При поступательном движении все точки тела движутся одинаково, поэтому достаточно изучить движение одной какой-то произвольной точки тела (например, движение центра масс тела), так же при поступательном движении тело не изменяет ни своего вида, ни строения, одновременные скорости всех точек равны и параллельны между собой, также равны и параллельны между собой ускорения всех точек. Враща́тельное движе́ние —движение, при котором все точки тела движутся по окружностям, центры которых лежат на 1 и той же прямой-ось вращения. Ось вращения может располагаться внутри тела и за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и следовательно имеют различные линейные скорости. Скорость- вектор первопроизводной по времени от радиуса вектора .Находящийся как отношение всего пути на все время . Характер быстрому применению и направлению движения мат.точки относитительно выбранной системой отсчета Ускорение-векторная величина ,характерно быстрому изменению скорости как по величине и по направлению

Поступательное движ → → → V = Vo + at → → → ² S = Vot + at/2 Vo-линейная скорость → А- полное ускорение T-время U=S/T U-скорость S-перемещение T-время

Вращательное движ W=Wo+Sl → ʮ = Wot+ £t²/2 Wo-угловая скорость

3.Динамика материальной точки. 1 закон Ньютона . Интегральные системы отсчета . 1. Динамика материальной точки

В качестве материальных объектов в механике рассматриваются материальная точка, абсолютно твердое тело и система материальных точек или тел. Материальной точкой называется точка, обладающая массой. Абсолютно твердое тело – это материальное тело, в котором расстояния между двумя любыми точками остаются неизменными. Механической системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех остальных.

Материальная точка - это модель материального тела любой формы, размерами которого в конкретной задаче можно пренебречь.

Первый закон динамики (закон инерции): материальная точка при отсутствии внешних воздействий сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные к ней силы не изменят этого состояния.

Законы динамики Галилея-Ньютона Первый закон Ньютона: существуют системы отсчета, в которых любое изолированное не подвергающееся действию внешних сил тело сохраняет свое состояние покоя или равномерного прямолинейного движения. Такие системы отсчета называются инерциальными.

4. 2 закон Ньютона . 3 закон Ньютона Второй закон Ньютона: ускорение движущегося тела прямо пропорционально действующей на него силе, обратно пропорционально массе тела и направлено по прямой, по которой эта сила действует, т. е.

где a – ускорение тела; F – сила; m – масса тела.

Сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного и прямолинейного движения. Масса тела выступает как коэффициент пропорциональности между силой, действующей на тело, и ускорением (F = ma) и характеризует инертность тела, т. е. степень неподатливости изменению состояния движения.

Третий закон Ньютона: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки, т. е.

где F₁₂ – сила, действующая на первое тело со стороны второго; F₂₁ – сила, действующая на второе тело со стороны первого.

Выдающейся заслугой Ньютона было открытие закона всемирного тяготения: два точечных тела притягивают друг друга с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной вдоль соединяющей их прямой, т. е.

где ? = 6,7 10^-11 м³/(кг • с²) – гравитационная постоянная; m₁ и m₂ – массы тел; r – расстояние между телами.   Третий закон Ньютона - два тела взаимодействуют между собой, с силами, равными по модулю и противоположными по направлению. Или сила действия равна силе противодействия.

5.Момент импульса . Момент силы . Уравнение моментов . Моментом силы относительно неподвижной точки назыв.векторным произведением,радиус R проведенного из точки О в точку приломленной силы на вектор силы Моментом импульса относит.неподвиж.точки назвы.вектор L,равный векторному произведению R этой точки на вектор импульса

6.Момент инеркции. Теор Штейнера. Основной закон динамики вращательного движения . Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Момент инерции
Размерность	L2M
Единицы измерения
СИ	кг·м²
СГС	г·см²

Теорема Гюйгенса — Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела Jотносительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

где m — полная масса тела.

7.Механическая работа. Кинетическая и потенциальная энергия. Мощность . Механическая работа-действие силы, связанное с перемещением тела, характеризуется механической работой.

Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы F на модуль перемещения   и на косинус угла   между ними

В СИ единицей работы является джоуль (Дж).

Кинетическая энергия

Когда сила, приложенная к телу, больше силы сопротивления, то результирующая сила приводит тело в движение. Движущееся тело обладает кинетической энергией.

Работа по ускорению тела тратится на увеличение его скорости, т.е. увеличение кинетической энергии:  K = 1/2(mV²)

Кинетическая энергия тела прямо пропорциональна его массе и скорости - кинетическая энергия тем больше, чем выше скорость и больше масса тела.

2. Потенциальная энергия  Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

 Потенциальная энергия - это энергия положения

: U = mgh 4. Мощность

Мощность - это скорость выполнения работы за единицу времени  P = W/t (Дж/с) или (Вт)

Мощность является скалярной величиной! Мощность равна произведению скорости и силы  P = FV (H·м/с) или (Вт)

8.Колебания.Гармонические колебания, их основные параметры . Уравнение гармонических колебаний .

Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени..

Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер ; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида

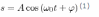
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А.

т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем

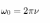
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.

9.Физ . И Мат. Маятники

Физ.маятник –твердое тело,которое может совершать колебания относительно неподвиж.гориз.оси не проход.через центр тяж.тела Ftp=O

M=-mgh sin A(альфа)

Мат.маятник-матер.точка подвеш.на тонкой нерастяж.нити(невесомой)

d=ƪ γ=mƪ²

T=2Π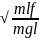

T=2gΠ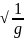

10.Виды деформации. Закон Гука. Модуль Юнга .

Деформация-это изменение формы и размера тел под действием внешних сил.

Различают два вида деформаций: упругие и пластические.

Упругой деформация называется, если после прекращения действия внешних сил тело принимает первоначальную форму и размеры.

Пластической деформация называется, когда тело после прекращения воздействия продолжает сокращаться Закон Гука: Величина упругой деформации пропорциональна действующей силе

, где К-жесткость пружины , ▲ƪ-деформация

Модуль Юнга- численно равен сили растягивающей стержень вдвое с единичной площадью поперечного сечения . Модуль Юнга зависит от свойств материала и не зависит от размеров и формы тела

Е= ,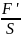

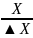
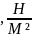
11.Гидродинамика идеальной жидкости. Уравнение неразрывности потока. Уравнение Бернулли

Идеальной называется абсолютно несжимаемая жидкость, не обладающая вязкостью.

Уравнение неразрывности жидкости.

Это такое движение жидкости, при котором в её потоке не возникает пустот. Для произвольных сечений элементарной струйки с площадью dS1,dS2….dSn, где жидкость течет со скоростью соответственно u1,u2…un расход жидкости одинаков : dQ1,= dQ2…=dQn

Подстановка в данное выражение позволяет получить уравнение неразрывности элементарной струйки жидкости :

U1 * dS1 = u2 * dS2 = …. = un * dSn = const

Для потока жидкости уравнение неразрывности имеет вид :

U * S = const

Уравнение Бернулли

Уравнение Бернулли можно вывести, используя закон сохранения энергии при описании течения жидкости в трубке. Для элементарной струйки идеальной жидкости уравнение Бернулли записывается в виде :

Где z1 z2 – геометрическая высота или геометрический напор в произвольных сечениях 1 и 2 элементарной струйки идеальной жидкости, u2 u1 – скорость элементарной струйки в сечении 1 и 2, p1 p2 – давление в сечениях 1 и 2 элементарной струйки, p – плотность жидкости. Закон Бернулли полное давление равное сумме статистич,динамич,весового давления в любой части потока идеальной жидкости остается поятоянной

12.Вязкость.Закон Ньютона для вязкости. Коэффициент вязкости . Закон Стокса . Внутренним трением(или вязкостью) называется свойство жидкостей или газов оказывать сопротивление при перемещении одной части жидкости относительно другой. это свойство жидкостей и газов количественно характеризуется коэф.вязкости ῃ(или просто вязкостью) .в ламинарном потоке жидкости(газа) сила трения F между двумя соседними слоями ,движущимися со скоростями ῡ и ῡ+dῡ, опис . формулой Ньютона : F=-ῃ∙S∙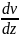 , где -градиент скорости потока в данном месте ,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости , а , следовательно , и поверхности соприкасающихся слоёв площадью S. Из формулы Ньютона следует , что =1с¯¹ и S=1м² ῃ=F,т.е вязкость численно равна тангенциальной силе, необходимой для поддержания разности скоростей,равной единице,между двумя параллельными слоями жидкости,расстояние между которыми равно единице.В Си ед.динам.вязкости явл. Па∙с.. Вязкость проявл и при движении твердых тел жидкости в самом простом случ.выраж.дается законом Стокса :F=6∙Π∙R∙ῃ∙ῡ

При движ.тела с сферич.формой в вязкой среде с малой скоростью на тело действует сила внутр.трения пропорц. Коэф .вязкости .