Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Тульский государственный университет

КАФЕДРА ЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРООБОРУДОВАНИЯ

Контрольно-курсовая

по методам оптимизации в электроснабжении

Вариант № 12

Выполнил: студент гр. Б161221

Филатов А.Р.

Проверил: д.т.н., проф.

Ловчаков В.И.

Тула 2016

СОДЕРЖАНИЕ

1. Постановка задачи синтеза ЦСУ………………………………………….…....4

2. Определение периода дискретизации………………………………………….5

3. Определение передаточной функции разомкнутой системы…..…………….7

4. Критический (граничный) коэффициент усиления замкнутой ЦСУ со стандартным П-регулятором………………………………………………......10

5. Расчет переходных процессов со стандартным П–регулятором…………....13

6. Синтез модального дискретного закона управления ...………………….…..15

Заключение……………………………………………………………..……....18

Список использованной литературы…………………………………………19

1. Постановка задачи синтеза цсу

Требуется найти и рассчитать систему таким образом, чтобы её выходная величина соответствовала заданию, причём выходила на требуемый уровень за определённое время с заданными параметрами качества, т.е. должно быть обеспечено соответствующее качество переходного процесса.

Выход на заданное значение при действии возмущения, приводящего к появлению ошибки, невозможен без наличия обратной связи, которая компенсирует возникающую ошибку, т.е. разницу между выходной величиной и заданием.

Переходный процесс, т.е. процесс от начала работы ЦСУ до её выхода на установившееся значение, также должен осуществляться с заданными технологическими показателями – временем переходного процесса, перерегулированием и статической ошибкой. Это обеспечивается введением управляющих алгоритмов – П, ПИ или ПИД-регуляторов. Кроме того, улучшение качества переходного процесса может быть достигнуто введением импульсного модального регулятора.

2. Определение периода дискретизации

Допустимая величина периода дискретизации T может быть определена 3 способами:

1. теорема Котельникова: для того, чтобы непрерывный сигнал с частотным спектром, ограниченным максимальной частотой , можно было точно восстановить по последовательности его дискретных значений, необходимо, чтобы частота квантования должна удовлетворять неравенству:

Т.к. , то

2. метод П.Т. Крутько

при

Из формул получаем следующие рекомендации для выбора периода квантования

3. метод М.Н. Мазурова

,

где – время достижения кривой разгона (т.е. переходной функции объекта) 95 % - ого уровня по отношению к установившемуся значению.

Для нашей системы цифрового управления воспользуемся методомП.Т. Крутько (для определения ) и теоремой Котельникова (для определения периода дискретизации Т).

Найдем амплитудно-фазовую характеристику (АЧХ):

,

где .

Т.е. .

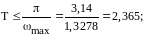
3. Определение передаточной функции разомкнутой системы.

Так как дискретные объекты описываются разностными уравнениями, а непрерывная часть – дифференциальным уравнением, то возникает задача построения дискретного описания системы, которая состоит в определении единого разностного уравнения, описывающего данную систему в целом.

Эта задача может решаться следующими способами:

1. непосредственная дискретизация дифференциальных уравнений.

Этот метод можно применять, когда , где – постоянная времени непрерывной части, причём он является весьма приблизительным;

2. дискретное преобразование Лапласа

3. Z-преобразование

Вводя обозначение , получаем

Рисунок 1 – Структурная схема ЦСУ

Получившуюся ЦСУ можно описать двумя способами:

1. С помощью дискретной передаточной функции:

,

причём (критерий устойчивости).

2. С помощью разностных уравнений:

Зная передаточную функцию, легко записать разностное уравнение, которым описывается данная система. Рассмотрим на примере передаточной функции IIпорядка:

.

Применяя основное свойство пропорции и подставляя замены:

, , , , , получаем:

Для расчёта переходных процессов это уравнение записывают в виде:

.

Определим дискретную передаточную функцию нашей разомкнутой системы (предполагается наличие экстраполятора нулевого порядка):

Используя подстановку , получим:

.

Тогда:

Найдём :

.

По методу Остроградского находим коэффициенты А, В и С:

;

Возвращаясь к выражению для , получаем:

.

Воспользовавшись таблицей Z-преобразований, получим:

.

Возвращаясь к выражению для W₀ и учитывая, что период дискретизацииТ=3,02с, получаем дискретную передаточную функцию нашей разомкнутой системы: