1. Определение задачи математического программирования. Задача линейного программирования, стандартная форма задачи линейного программирования, каноническая форма задачи линейного программирования.

Математическое программирование - это область математики, разрабатывающая теорию, решения многомерных задач с ограничениями. В отличие от классической математики, мы находим наилучший вариант из всех возможных.

Итак, математическое программирование — это раздел высшей математики, занимающийся решением задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.

Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

Классическая задача математического программирования – задача выбора таких значений некоторых переменных, подчиненных системе ограничений в форме равенств, при которых достигается max или min функции

Общий вид задачи ЛП:

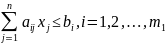
Стандартная форма:

Каноническая форма:

ОБОЗНАЧЕНИЯ: n – Число продуктов (производства, питания, продажи итд)

m – Число ресурсов (имеющихся веществ, товаров)

i, j – виды ресурсов

– Количество ресурсов i-го вида, необходимых для производства продукта j-го вида

– запасы ресурсов i-го вида

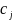- цена продукта j-го вида,

2. Допустимое решение задачи, область допустимых решений, оптимальное решение задачи. Целевая функция, градиент.

Допустимым решением задачи называется любой n-мерный вектор

x (x = ( , ,…, )), удовлетворяющий системе ограничений и условию неотрицательности.

Множество допустимых решений образует ОДР.

Оптимальным решением задачи называется такое допустимое решение, при котором целевая функция достигает экстремума (то есть, своего максимума, либо минимума).

Целевая функция — вещественная или целочисленная функция нескольких переменных, подлежащая оптимизации (минимизации или максимизации) в целях решения некоторой задачи математического программирования.

Чаще всего имеет вид:

F (x)= c1x1 + c2x2 + ... + cnxn → max(min)

Градие́нт — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.

3. Экономико-математические модели задач лп: задача о банке.

К экономико-математическим моделям задач ЛП относятся: Задача планирования производства, определения оптимального ассортимента продукции, о диете, о банке, составления жидких смесей, Транспортная задача

Задача о банке:

Собственные средства банка в сумме с депозитами составляют 100 млн. $. Не менее 35 млн. $ из этой суммы размещена в кредитах (не ликвид). Ликвидное ограничение ценных бумаг должны составлять не менее 30 %, размещенных в кредитах и ликвидных активах.

Пусть – средства, размещенные в кредитах, – средства, размещенные в ликвидных активах.

Банковское ограничение: (т.к. средства банка равны 100млн. и больше этого числа использовать нельзя)

Кредитное ограничение:

Ликвидное ограничение

, ≥ 0 – Условие неопределенности

F = c1x1 + c2x2 max, где с1 – доходность кредитов, с2 – доходность ценных бумаг.