1.1.6 Теплоемкость газов

Подвод (или отвод) тепла к телу в процессе вызывает измене­ние параметров состояния, главным образом температуры. Поэтому для вычисления количества тепла при изменении состояния тела мож­но использовать изменение температуры и величину, характеризующую свойства тела. Величина, характеризующая способность тела изменять температуру в процессах с подводом (или отводом) тепла называет­ся теплоемкостью.

Теплоемкостью тела называется количество тепла, ко­торое необходимо подвести (или отвести) к телу, чтобы изменить его температуру на 1 К.

Удельной теплоемкостью называется теплоемкость, отнесенная к единице массы вещества.

Понятие теплоемкости используется для вычисления количества тепла участвующего в процессе.

В зависимости от того, к какой единице массы относится тепло­емкость, различают три вида удельной теплоемкости.

Массовой теплоемкостью называется удельная теплоемкость, от­несенная к 1 кг массы газа. Она обозначается С и имеет раз­мерность Дж/(кг· K), кДж/(кг·K).

Объемной теплоемкостью называется теплоемкость, отнесенная к массе газа, содержащегося в 1 м³ газа, взятом при нормальных ус­ловиях. Она обозначается с^/ и имеет размерность Дж/(нм³·К), кДж/(нм³·К).

Киломольной или молярной теплоемкостью называется теплоем­кость, отнесенная к 1 киломолю газа. Она обозначается μС и имеет размерность Дж/(кмоль·K).

Связь между разными видами удельной теплоемкости следующая:

где υ_Н – удельный объем газа, взятого при нормальных усло­виях и равный м³/кг.

Исходя из принятой характеристики удельной теплоемкости, количество тепла в процессе может быть определено по следующим формулам:

где – число киломолей рабочего тела;

– объем рабочего тела при нормальных условиях, м³.

Приведенные уравнения справедливы при условии постоянного значения теплоемкости в заданном интервале температур, либо если теплоемкость принимается постоянной условно.

В действительности теплоемкость изменяется в зависимости от вида процесса, в котором участвует газ, а для данного процесса изменяется с изменением температуры. Графическая зависимость теплоемкости от температуры представлена на рисунке 1.1.

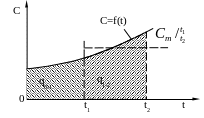
Рисунок 1.1 – Зависимость теплоемкости газа от температуры

Для бесконечно малого участка зависимости С = f(t) истинная теплоемкость при данной температуре тела t, для 1 кг массы может быть определена из условия:

откуда: .

При изменении темпера­туры рабочего тела в про­цессе от t₁ до t₂ количество тепла участвующе­го в процессе на 1 кг мас­сы тела будет равно:

где, очевидно, что: C = f(t).

Величина истинной теплоемкости, определяется для разных ве­ществ экспериментальным путем и обычно выражается степенной зави­симостью вида:

где a₀ , a₁ , a₂ , a₃ – эмпирические коэффициенты.

Для упрощения практических расчетов по определению количест­ва тепла вводится условное понятие средней удельной теплоемкости тела в данном процессе, которая для 1 кг массы в интервале темпе­ратур от t₁ до t₂ будет равна:

.

Использование средней теплоемкости облегчает задачу вычисле­ния количества тепла в процессе, т.к. в этом случае:

.

Значения средней теплоемкости также определяются экспери­ментальным путем, а для расчетов задаются в виде таблиц или эм­пирических зависимостей.

Так как в практических расчетах может потребоваться значение средней теплоемкости в любом интервале температур, то в таблицах и формулах задается значение средней теплоемкости с фиксированным нижним пределом, равным 0°С, т.е. средняя теплоемкость задается только в интервале температур от 0° до t °С, и может быть использована для расчета количества тепла в любом интервале температур путем следующего преобразования. Из условия следует, что:

откуда средняя теплоемкость в данном интервале температур равна:

.

Величина теплоемкости сильно зависит так же от условий про­текания процесса и для каждого процесса имеет свое определенное значение. При этом ее значение меняется от ± (для изотерми­ческого процесса, dT=0) до 0 (для адиабатного процесса, dq=0). Так как число различных термодинамических процессов бесконечно велико, то также велико и число значений теплоемкости в процессах. Для вычисления величины теплоемкости в любом процессе вводятся две основные, стандартные теплоемкости для двух, (принятых за опорные значения) процессов. Это теплоемкость в процессах, протекающих при постоянном давлении, она обозначается С_р и теплоемкость при постоянном объеме – С_υ .

Связь между ними устанавливается уравнением Майера:

С_р – C_υ = R, кДж/кг·К – для 1 кг газа;

μC_p – μC_υ = 8,3142 , кДж/Кмоль·К – для 1 кмоля.

В термодинамике часто используется также отношение:

которое называется коэффициентом Пуассона.

В таблицах и эмпирических формулах для истинных и средних теплоемкостей задаются только два значения теплоемкости С_р или С_υ , a теплоемкость в остальных процессах вычисляется с их помощью в зависимости от характеристики данного процесса.

При обозначениях теплоемкостей учитываются указанные выше обозначения ее видов. Например, μC_υ – истинная, киломольная теплоемкость при постоянном объеме, – средняя, объемная теплоемкость при постоянном давлении и т.д.

Теплоемкость газовых смесей определяется как сумма теплоем­костей входящих в ее состав компонентов с учетом их количествен­ных соотношений.

Для 1 кг смеси газов, массовая теплоемкость будет равна:

.

Для 1 нм³ смеси газов, объемная теплоемкость будет равна:

.