2.1 Теплопроводность

0. 2.1.1 Основные определения

Процесс распространения тепловой энергии (теплопроводность) в твердом теле есть функция изменения температуры внутри этого тела.

В свою очередь, температура в любой точке тела при установившемся режиме есть функция координат этой точки .

Температурным полем называется совокупность всех значений температур во всех точках рассматриваемого тела.

Изотермической поверхностью называется поверхность, соединяющая в пространстве две точки с одинаковой температурой. Изотермические поверхности не пересекаются между собой, не имеют разрывов и скачков и в общем случае имеют произвольную форму.

Температурное поле в общем случае трехмерное.

В простейшем случае температурное поле одномерное, то есть температура изменяется в направлении одной оси; изотермические поверхности есть плоскости, перпендикулярные оси; температурный градиент направлен вдоль оси, температурный градиент направлен вдоль оси в положительную сторону.

Распространение тепла идет всегда в сторону убывания температуры.

Характеристиками температурного поля в любой его точке являются две величины:

– градиент температуры , характеризующий интенсивность изменения температуры по расстоянию;

– удельный тепловой поток , характеризующий интенсивность переноса тепловой энергии по направлению.

Температурным градиентом называется вектор, показывающий интенсивность изменения температуры в направлении нормали к изотермической поверхности в данной точке А, равный:

, (2.1)

где – изменение температуры;

– соответствующее этому температурному перепаду изменение расстояния.

Этот вектор направлен в сторону увеличения температуры.

Расчетная схема температурного поля к определению градиента температуры представлена на рисунке 2.1.

Рисунок 2.1 – Расчетная схема градиента температурного поля

Удельным тепловым потоком или поверхностной плотностью теплового потока называется вектор, определяющий количество тепловой энергии, проходящей в единицу времени через единицу площади изотермической поверхности в направлении нормали в данной точке. В общем случае величина удельного теплового потока будет равна:

Этот вектор направлен в сторону понижения температуры.

1.1.2 Основной закон теплопроводности – закон Фурье

Закон Фурье устанавливает связь между характеристиками температурного поля в любой его точке.

Удельный тепловой поток при теплопроводности пропорционален градиенту температуры и направлен в обратную сторону по отношению к градиенту температуры. Математическое выражение закона Фурье имеет вид:

. (2.2)

Знак (–) учитывает, что вектор теплового потока направлен противоположно вектору градиента температур.

Коэффициент пропорциональности называется коэффициентом теплопроводности (Вт/м×град) и является важной характеристикой способности тел передавать или задерживать тепло при теплопроводности. = 400 – 500 Вт/м×град для металлов (медь – сталь), применяемых в теплообменниках, = 0,2 ¸ 0,05 Вт/м×град – для теплоизоляционных материалов.

Уравнение Фурье дает математическое описание произвольного температурного поля в дифференциальной форме.

Для получения расчетных зависимостей процесса теплопроводности в конкретных условиях необходимо дифференциальное уравнение Фурье дополнить математическим описанием всех частных особенностей конкретного процесса.

Таковыми особенностями являются условия однозначности (размеры, форма, физические характеристики тела, температурные условия и т. д.) и краевые условия (начальные и граничные условия).

В качестве примера рассматривается решение задачи теплопроводности для наиболее простых, но практически важных случаев – теплопроводность плоской и цилиндрической стенки в стационарных условиях.

2.1.3 Теплопроводность плоских стенок

а)Теплопроводность в однослойной плоской стенке

Рассмотрим однородную плоскую стенку с толщиной , м и коэффициентом теплопроводности материала стенки , представленную на рисунке 2.2.

Температурное поле в плоской стенке одномерное, а его градиент направлен по нормали к стенке, совпадающей с осью Х. Изотермические поверхности в этом температурном поле представляют собой плоскости, параллельные наружным поверхностям стенки. Температура на левой поверхности стенки во всех точках равна t_ст1, на правой – t_ст2 . Поток тепла направлен от t_ст1 к t_ст2, и его величина постоянна для всей стенки, так как площадь всех изотермических поверхностей одинаковая.

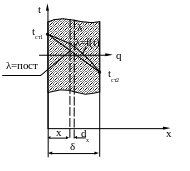
Рисунок 2.2 – Схема температурного поля однослойной плоской стенки

Установим начало координат на левой поверхности стенки и выделим на расстоянии две изотермические поверхности на расстоянии друг от друга при изменении температуры на .

Уравнение теплопроводности (закон Фурье) для слоя будет иметь вид:

.

Разделяя переменные, получим:

.

Интегрируя полученное дифференциальное уравнение, будем иметь:

.

Из полученного уравнения следует, что, при температура в плоской стенке изменяется по линейному закону (рисунок 2.2).

Постоянная интегрирования находится из граничных условий:

– при Х = 0 t = t_ст1;

– при Х = t = t_ст2.

Подставляя первое граничное условие, имеем:

С = t_ст1 и .

Подставляя второе граничное условие, получим уравнение вида:

.

Решая полученное уравнение относительно величины , получим зависимость для определения теплового потока в плоской стенке:

. (2.3)

Обозначим величину , К·м²/Вт и назовем ее термическим сопротивлением плоской стенки, тогда уравнение теплового потока для плоской стенки примет вид:

. (2.4)

Уравнение теплопроводности в таком виде аналогично закону Ома для проводника, где тепловой поток соответствует силе тока, – разности потенциалов – движущей силе процесса, а R – электрическому сопротивлению.

Строительные и теплоизоляционные материалы имеют низкий коэффициент теплопроводности, зависящий от температуры материала. Обычно эту зависимость представляют в следующем виде:

. (2.5)

В этом случае уравнение теплопроводности будет иметь вид:

.

Разделяя переменные, получим выражение:

,

что после интегрирования дает:

.

Определяем постоянную интегрирования из принятых граничных условий. После подстановки приходим к выражениям вида:

;

;

.

Если представить величину , то приходим к выражению:

, и . (2.6)

б) Теплопроводность в многослойной плоской стенке

На практике плоская стенка встречается наиболее часто в виде многослойной конструкции с параллельными плотно прилегающими слоями.

Рассмотрим многослойную плоскую стенку, состоящую из однородных параллельных слоев с толщиной и коэффициентом теплопроводности в каждом слое. Температура на наружной поверхности первого слоя во всех точках равна , на поверхности последнего слоя – . Тепловой поток – постоянная величина для всех слоев и направлен в сторону понижения температуры.

Схема температурного поля такой многослойной плоской стенки представлена на рисунке 2.3.

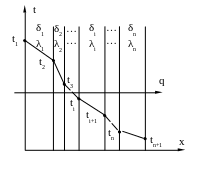
Рисунок 2.3 – Схема температурного поля многослойной плоской стенки

Запишем уравнения теплопроводности для каждого слоя в отдельности и представим их в виде системы:

Решая полученные уравнения относительно разности температур и складывая почленно их левые и правые части, после сокращения одинаковых температур с разными знаками, будем иметь:

Тогда уравнение теплового потока можно представить в виде:

Обозначим выражение в знаменателе как – термическое сопротивление многослойной стенки. Тогда уравнение теплового потока окончательно примет вид:

_(2.7)

По аналогии с последовательным соединением электрических проводников, термическое сопротивление многослойной стенки равно сумме термических сопротивлений всех ее отдельных слоев.

Для определения температуры в любом промежуточном слое t_i+1 используем условие постоянства теплового потока при любом числе слоев:

,

откуда получаем выражение:

_(2.8)