10. Числовые характеристики случайных величин.

-математическое ожидание и дисперсия случайной величины;

Опр. Мат.ожидание случайной величины Х наз-ся ее среднее значение, если это значение существует. M(X)=mx=m

MX=

Условие существования мат. Ожидания

f(x)dx

Св-ва мат.ожидания:

1)Mc=c, c-const

2)M(aX+b)=aMX+b

3)M(X+Y)=MX+MY

4)M(XY)=MX*MY, тогда и только тогда, когда Х и У независимые случайные величины

Опр. Дисперсией случайной величины называется 2ой момент центрированной случ. Величины

DX=M(X-MX)²

DX=MX²-(MX)²=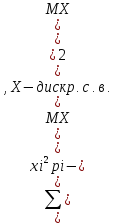

Свойства дисперсии:

1)DX≥0

2)DC=0, c=const

3)D(aX+b)=a²DX

4)D(X+Y)=DX+DY, тогда и только тогда, когда X и Y неависимые случайные величины

- мода, медиана, квантиль;

Опр. Модой случайной величины наз-ся наиболее вероятное значение среди всех ее возможных значение М0(Х)

Если распределение непрерывное, то мода-это точка максимума плотности распределения

Если дискретное,то мода-это значение которое случ.величина принимает с наибольшей вероятностью

Опр. Медианой непрерывной случ.величины наз-ся число, которое делит всю область возможных значений на 2 части таким образом, что вероятность того, что значение случайной величины превысит медиану будет равно вероятности того, что оно будет меньше медианы

P{X<Me(X)}=P{X>Me(X)}=1/2

Опр. Квантиль Xp уровня р - это число определеяемое из уровня F(xp)=p.

F-функция распределения случ.величины, т.е. квантиль Хр – такое число, для которого вер-ть события, что случ. величина X окажется меньше этого числа равна величине уровня р.

P{X< Xр}=р

Для наиболее важных распределений представлены таблицы квантилей.

- начальные и центральные моменты k-ого порядка случайной величины.

Начальный момент порядка k

m_k = M =

центральный момент порядка k – мат.ожидание k-ой степени центрированной СВ

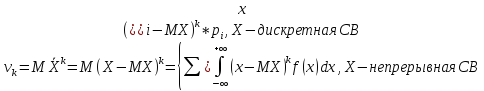
12.Предельные теоремы ТВ охватывают круг вопросов, связанных с поведением средних значений и их распределений в ситуациях, когда неограниченно возрастает количество случайных событий, участвующих в формировании величин. Эти теоремы имеют чрезвычайно большое теоретическое и практическое значение; создают теоретическое обоснование статистического определения вероятности; на них опирается весь аппарат мат.сатистики и ее приложений.

Неравенство Чебышёва

Пусть случайная величина Х имеет конечное мат.ожидание и дисперсию, тогда для любого положительного числа верно:P{|X - MX|≥ԑ}≤

Вероятность того, что случайная величина Х отклонится от мат.ожидания МХ не меньше, чем на , не больше отношения дисперсии к.

Теорема Чебышёва (закон больших чисел)

Пусть случайные величины Х₁, Х₂, … , Х_n независимы и их дисперсии равномерно ограничены, т.е. DX_i ≤ 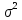,i=1, 2,…, тогда для любого > 0:

ԑ} = 1, где

среднее арифметическое случайных величин (величина случайная)

среднее арифметическое мат.ожиданий (неслучайная величина – детерминированное число)

Последовательность средних арифметических n случайных величин сходится по вероятности к среднему арифметическому их мат.ожтданий.

Следствие: Пусть случайные величины Х₁, Х₂, … независимы и одинаково распределены (MX_i = m, DX_i=,i=1,2…), тогда для любого :

ԑ} = 1, т.е. среднее арифметическое случайных величин сходится по вероятности к мат.ожиданию m.

Следствие теоремы Чебышёва обосновывает принцип среднего арифметического случайной величины X_i.

Пусть произведено n независимых измерений некоторой величины, истинное значение которой m неизвестно, результат каждого измерения есть случайная величина X_i, тогда в качестве приближенного значения величины m можно взять среднее арифметическое результатов измерений

m = =,причем равенство тем точнее, чем больше n.

На теореме Чебышёва основан также выборочный метод: о качестве большого количества однородного материала можно судить по небольшой его пробе. Закон больших чисел подтверждает связь между случайностью и необходимостью: среднее значение случайной величины = , почти НЕ отличается от неслучайной величины.

Следствия из закона больших чисел

1. Центральная предельная теорема (теорема Ляпунова)

Пусть случайные величины Х₁, Х₂, … независимы, одинаково распределены и имеют конечные мат.ожидания MX_i = m и дисперсии DX_i = .

Рассмотрим центрированные и нормированные случайные величины Y_n

Y_n = ; MY_n=0; DY_n=1, тогда P{Y_n < x}, где n

То есть сумма индивидуально малых случайных величин с ростом числа слагаемых сходится к нормальной функции распределения.

Если исход опыта определяется большим числом случайных факторов, влияние каждого из которых описывается нормальным распределением с соответственным образом подобранными мат.ожиданием и дисперсией.

2. Локальная теорема Муавра-Лапласа

Пусть производится опыт в схеме Бернулли.

Если число опытов n , то для вероятности того, что число успеховX будет равно m, верно равенство: P{X=m},

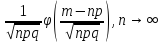где - плотность нормального распределения.

3. Интегральная теорема Муавра-Лапласа

Пусть производится опыт в схеме Бернулли. Тогда вероятность того, что число успехов Х попадет в интервал (m₁, m₂) может быть определена по формуле: P{m₁ < X < m₂}

13.Мат.статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей.

Предметом мат.статистики является изучение случайных величин по результатам наблюдения.

Задачи мат.статистики: 1. Обработка экспериментальных данных

2. оценивание характеристик

3. проверка статистических гипотез

Генеральная совокупность – множество всех подлежащих изучению объектов или возможных результатов всех наблюдений, производимых в неизменных условиях над одним объектом.

Выборочная совокупность (выборка) – множество объектов, отобранных случайным образом из генеральной совокупности.

Объем выборки – число объектов в ней.

Выборочный метод – метод статистического исследования, состоящий в том, что на основе выборочной совокупности делается заключение о генеральной совокупности.

Выборка репрезентативна (представительна) если соблюдается случайность отбора, т.е. все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку.

Вариационный ряд выборки – упорядоченная в порядке возрастания перестановка элементов выборки.

Процедура упорядочивания называется ранжированием, а номер элемента выборки в вариационном ряду – рангом элемента.

Размах выборки d = x_max - x_min

Если среди элементов выборки имеется r различных чисел z₁, z₂, … , z_r и число z_i, встречается n_i раз, то z_i – варианта, а n_i – частота.

Статистический ряд – таблица из двух строк, в которой в верхней строке находятся упорядоченные в порядке возрастания варианты z_i, а во второй строке – соответствующие частоты n_i. ∑n_i = n, где n – объем выборки.

Относительная частота варианты x_i – число, равное ; W_i .

Пусть х – некоторое число, тогда число вариант n_x, значение которых <x, называется накопленной частотой. n_x = .

Статистические ряды бывают дискретными и интервальными.

Интервальный (группированный) статистический ряд – ряд, в котором весь размах выборки разбит на некоторое количество промежутков x_i-1 < x < x_i, причем соседние элементы вариационного ряда, принадлежащие одному промежутку, не различаются по величине – им назначается одна варианта, представляющая весь интервал (обычно середины интервала), а их общее число составляет частоту, назначаемую этой варианте. Если варианта находится на границе интервала, то ее присоединяют к левой границе. При выборе способа разбиения, обычно, но не обязательно, выбирают интервалы одинаковой ширины. При выборе числа интервалов обычно, но не обязательно, пользуются правилом Стерджеса: r.

Выборочная (эмпирическая) функция распределения F*(x) – функция, значение которой в точке х равно накопленной частоте. F*(x) = .

Графические представления выборки

Пусть дан дискретный статистический ряд

Полигон частот – ломаная, соединяющая точки плоскости с координатами (x_i;n_i).

Пусть выборка задана интервальным статистическим рядом.

Гистограмма частот – ступенчатая фигура из прямоугольников с основаниями, равными длине интервала , и высотами, равными h_i = ;S = n.

Гистограмма относительных частот (эмпирическая плотность распределения f*(x)) – фигура из прямоугольников с основаниями и выстотами h_i = ;S = 1.

Выборочные (эмпирические) числовые характеристики – это приближенные значения соответствующих числовых характеристик генеральной совокупности, определяемые по выборке.

Выборочное среднее (выборочное мат.ожидание) – среднее арифметическое результатов наблюдений. (интервальный статистический ряд);(дискретный статистический ряд).

Выборочное среднее дает приближенное значение мат.ожидания генеральной совокупности.

Выборочная дисперсия – число, определяемое формулой:

. Выборочная дисперсия служит приближенным значением дисперсии генеральной совокупности.

, где =.

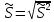- выборочное СКО, которое дает приближенное значение для СКО генеральной совокупности.

Наряду с выборочной используется уточненная (исправленная) выборочная дисперсия

14.Основная задача мат.статистики состоит в нахождении конкретных законов распределения вероятности наблюдаемой случайной величины Х по данным выборки. Во многих случаях вид распределения можно считать известным, и задача сводится к получению приближенных значений неизвестных параметров этого распределения.

F(x, ) – функция распределения случайной величины Х, содержащая 1 неизвестный параметр .

Любая функция элементов выборки называется статистикой или статистической оценкой. – значение по выборке; (x₁, … ,x_n)

Точечной оценкой неизвестного параметра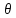 называется приближенное значение этого параметра, полученное по выборке. Точечная оценка означает, что оценка представляет собой единственное число, которое изображается точкой на числовой оси.

Критерии качества статистических оценок

1. Несмещенность: - оценка называется несмещенной оценкой , если ее мат.ожидание М(равно оцениваемому параметру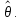

- М() - - смещение

- испольвание смещенной статистической оценки приводит к систематической ошибке, т.е. к неслучайной ошибке, искажающей оценки результатов измерений в одну определенную сторону, поэтому соблюдение требования несмещенности гарантирует от влияния систематических ошибок при вычислении оценки .

2. Состоятельность: (x₁, … ,x_n)

- оценка _n называется состоятельной оценкой , если _n сходится по вероятности к при увеличении объема выборки

- для любого ԑ > 0

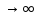Теорема: Если М(_n) иD(_n) ,n , то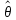_n – это состоятельная оценка параметра .

3. Эффективность: - несмещенная оценка называется эффективной в классе оценок_i, если она имеет наименьшую дисперсию:

D() =

Теорема 1. Выборочное среднее называется несмещенной, состоятельной и эффективной оценкой мат.ожидания в классе всех линейных оценок.

Теорема 2. Выборочная дисперсия 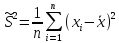является смещенной оценкой генеральной дисперсии, т.к. можно показать, чтоM() =, но исправленная выборочная дисперсияявляется несмещенной, состоятельной и эффективной оценкой в классе всех квадратных оценокM() =, где.

Замечание: Оценку нужно использовать во всех случаях, когда использование оценкиможет повлиять на значение цифры результата.

Точечные оценки математического ожидания и дисперсии

Выборочное среднее (выборочное мат.ожидание) – среднее арифметическое результатов наблюдений. (интервальный статистический ряд);(дискретный статистический ряд).

Выборочное среднее дает приближенное значение мат.ожидания генеральной совокупности.

Выборочная дисперсия – число, определяемое формулой:

. Выборочная дисперсия служит приближенным значением дисперсии генеральной совокупности.

, где =.

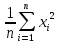- выборочное СКО, которое дает приближенное значение для СКО генеральной совокупности.

Наряду с выборочной используется уточненная (исправленная) выборочная дисперсия

Выборочный начальный момент порядка k

ν_k =

Выборочный центральный момент порядка k

μ_k =

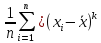
Выборочный центральный момент второго порядка равен выборочной дисперсии.

Точечная статистическая оценка вероятности случайного события

Предположим, что в некотором эксперименте событие А (благоприятный исход испытания) происходит с вероятностью p и не происходит с вероятностью q = 1 — р. Задача состоит в получении оценки неизвестного параметра распределения по результатам серии n случайных экспериментов. При заданном числе испытаний n количество благоприятных исходов m в серии испытаний — случайная величина, имеющая распределение Бернулли. Обозначим ее буквой μ.

Если событие А в серии из n независимых испытаний произошло m раз, то оценку величины предлагается вычислять по формуле:.

Выясним свойства предлагаемой оценки. Поскольку случайная величина μ имеет распределение Бернулли, то Μμ=np и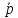 M= M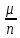= р, т.е. налицо несмещенная оценка.

Для испытаний Бернулли справедлива теорема Бернулли, согласно которой

, т.е. оценка p состоятельная.

Доказано, что эта оценка эффективна, так как обладает при прочих равных условиях минимальной дисперсией.

16.Доверительным интервалом для параметра , соответствующему доверительной вероятности γ, называется интервал (_н;_в), где _н – нижняя граница дов.инт., _в – верхняя граница дов.инт. они определяются по выборочным данным x₁, … , x_n, так, чтобы P{_н < <_в} = γ, т.е. вероятность того, что фиксированное значение содержится внутри интервала (_н;_в) равна доверительной вероятности γ.

Доверительный интервал, удовлетворяющий этим требованиям, называется интервальной оценкой параметра .

γ – доверительная вероятность, уровень доверия, надежность.

γ приближено для тех опытов, при многократном повторении в которых дов.инт. включает в себя истинное значение параметра .

Число γ выбирается так, что события с вероятностью α =1 – γ считается практически невозможными, где число α – уровень значимости.

Ширина интервала 2ԑ = _в – _н определяет точность оценки, а вероятность γ определяет достоверность оценки.

При фиксированном объеме наблюдений n нельзя одновременно увеличивать γ и уменьшать ԑ. Значение ԑ увеличивается с повышением достоверности γ, т.е. увеличивается погрешность оценки, и наоборот. Если при данной величине γ надо получить более узкий дов.инт., необходимо увеличить n.

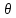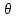Если выбрана некоторая оценка параметраиF(x) – функция распределения этой оценки, то границы _н и _в определяются: F(_н) = ;F(_в) = , т.е. _н и _в являются квантилями уровней и функции распределения F(x).

Основные распределения, используемые в методе интервальных оценок

1. Нормальное распределение

Если X N(m, ), тоf(x) = ,функция Лапласа

Соотношение между квантилями: Z_p = -Z_1-p, где = 1 -

2. Хи-квадрат распределение (распределение Пирсона)

Распределением сk степенями свободы называется распределение случайной величины Х_k равной сумме квадратов k независимых нормально распределенных по нормальному закону N (0,1) случайных величин U_i, i=1,2,… , k: X_k = =

Теорема

Пусть х₁, … , х_n – выборка из нормального распределения генеральной совокупности N (m, ) ии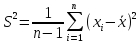– это выборочное среднее и исправленная выборочная дисперсия, тогда статистикии- независимые случайные величины, причем статистикаимеет- распределение с (n-1) степенью свободы.

3. Распределение Стьюдента

Распределением Стьюдента с k степенями свободы называется распределение случайной величины T_k равной отношению двух независимых случайных величин U и :T_k = , где U N(0,1), X – имеет – распределение сk степенями свободы.

Соотношение квантилей: t_p = t_1-p, p > 0,5.

4. F – распределение (распределение Фишера – Снедекора)

F – распределением с k₁ и k₂ степенями свободы называется распределение случайной величины F_{k1, k2} равной отношению двух независимых случайных величин и;, гдеимеют– распределение сk₁ и k₂ степенями свободы соответственно.

Соотношение квантилей: f_1-p(k₁; k₂) = .

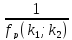Доверительный интервал для математического ожидания

1. При известной дисперсии

Дано: а) выборка x₁, … , x_n объема n из нормального распределения генеральной совокупности с известной дисперсией

б) доверительная вероятность γ

(–*;+*), где– квантиль нормального распределения уровня,α = 1 – γ.

2. При неизвестной дисперсии

Дано: а) выборка x₁, … , x_n объема n из нормального распределения генеральной совокупности

б) доверительная вероятность γ

(x – (n-1)*;x + (n-1)*) , гдеS = ,- исправленная выборочная дисперсия;- квантиль распределения Стьюдента уровнястепенью свободы.

Доверительный интервал для дисперсии

1. При известном мат.ожидании

Дано: а) выборка x₁, … , x_n объема n из нормального распределения генеральной совокупности с известным мат.ожиданием m

б) доверительная вероятность γ

(;, где=, где- квантиль– распределения с n степенями свободы уровня p.

2. При неизвестном мат.ожидании

Дано: а) выборка x₁, … , x_n объема n из нормального распределения генеральной совокупности

б) доверительная вероятность γ

;

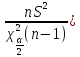
Доверительный интервал для параметра p Биномиального распределения

Дано: 1. n - число опытов, проводимых по биномиальной схеме

2. k - число успехов

3. α – уровень значимости

(, где- точечная оценка параметраp ();- квантиль нормального распределения уровня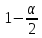.