2.Теорема умножения для n-событий

Р(А1,А2,…Аn)=

1.Вероятность произведения n-независимых событий равна произведению вероятностей этих событий

2.Вероятность произведения n-независимых событий равна произведению вероятностей этих событий причем, вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие произошли

теоремы сложения случайных событий

1).для 2х событий

Р(А+В)=

1)Вероятность суммы 2х несовместных событий равна сумме вероятностей этих событий

2)Вероятность суммы 2х совместных событий равна сумме вероятностей этих событий минус вероятность совместного появления

2)для n-событий

P(=P(Ai*…*An), если A1…An – совместные

Следствие 3

1)Вероятность суммы n-несовместных событий равна сумме вероятностей этих событий

2)Вероятность суммы n-совместных событий равна сумме вероятностей этих событий минус сумма вероятностей того, что события появляется парами AiAjAk минус и тд с соответсвующим знаком последний член: вероятность совместного появления всех событий

Следствие

Р(А+В+С)=Р(А)+Р(В)+Р(С) – Р(АВ)-Р(АС)-Р(ВС)+Р(АВС)

Сумма вероятностей событий образующих полную группу равна 1, если Ai…An – полная группа, то

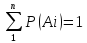
7.Схема гипотез. Формула полной вероятности. Формула Байеса

Формула полной вероятности

Пусть событие А происходит одновременно с одним из событий Н1…Нn –гипотезы

Гипотезы должны удовлетворять след. условиям

Полная группа событий

Пусть известны вероятности гипотез P(H1)…P(Hn) и условная вероятность события А при каждой гипотезе

Р(А|Н1)…Р(А|Hn),тогда вероятность события А можно найти по формуле полной вероятности

Р(А)=

Формула Байеса

Пусть события А происходят одновременно с одним из событий Н1…Нn, где H1…Hn- образуют полную группу

H1…Hn – несовместны и

H1…Hn – гипотезы

Пусть известны : P(Hi); P(A/Hi), i=1,…n

О результатах опыта есть неполная информация. Требуется найти вероятность гипотезы Hi после опыта

Апостернорная вероятность ( послеопытное) Р(Hi/A)

Априорная вероятность ( доопытная) Р (A/Hi)

Р(Hi/A)=формула Байеса

Где Р(А) - находится по ф-ле полной вероятности

8. Последовательность независимых испытаний

определение серии независимых испытаний;

Опр. Несколько опытов наз-ся независимыми, если их исходы представляют собой независимые события

формула (схема)Бернулли.

Схема последовательных испытаний: производится n-одинаковых и независимых опытов. В каждом из которых может произойти собтие А.

Вероятность того, что событие А произойдет в одном опыте равна p, p- вероятность успеха. q=1-p – вероятность неудачи в одном опыте

Вероятность того, что в n- опытах наступит m успехов определяется по формуле Бернулли

Pn(m)= , m=0, 1 … n

Опр. Наивероятнейшее число k0 наступления события А в схеме Бернулли определяется след. нер-вом np-q ≤ k0 ≤np+p

9. Случайные величины. Их виды и характеристики

Под случайной величиной понимается величина, принимающая в результате опыта какое либо числовое или качественное значение.

Основными характеристиками случайной величины, заданной своими распределениями, является математическое ожидание ( или среднее значение ) и дисперсия.

Математическое ожидание случайной величины является центром ее распределения. Дисперсия характеризует отклонение случайной величины от ее среднего значения.

определение непрерывной и дискретной случайной величины;

Опр.Случайная величина – это число, определяемое в случайном опыте

Случайная величина полностью определена, если известен исход опыта

Опр. Случ величина Х – это ф-ия ставящая в соответсвие каждому элементарному исходу определенное число

- функция распределения случайной величины и ее свойства;

С каждой случ. Величиной связывают ее ф-ию распределения

F(x) случайной величины Х – это ф-ия, значение которой в точке х равно вероятности события {X < x}

F(x)=P{X < x}

Св-ва ф-ий распределения

1. 0≤F(x) ≤1

2. )=0

)=1

3. ∀x1≤x2

F(x1) ≤F(x2)

Т.о F(x) неубывающая функция

4)F(x) – непрерывна слева (справа)

- плотность распределения вероятностей непрерывной случайной величины и ее свойства;

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения. Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.

Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:

P{a ≤ X ≤ b} =

В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f(x) и опирающейся на участок (α,β)

Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:

F(x) =P{X < x} = P{ -∞< X < x =