Скользящее отражение пространства

Литература

Таблица8

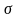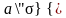Композиция симметрии относительно плоскости и параллельного переноса на вектор а, где называется скользящим отражением (СО).

Свойства:

1. СО сохраняет расстояния между любыми точками.

2. СО сохраняет простое отношение трех точек.

3. СО переводит плоскость в плоскость, причем параллельные плоскости в параллельные; полупространство в полупространство; прямую в прямую, причем параллельные прямые в параллельные; полуплоскость в полуплоскость, отрезок в отрезок, луч в луч.

4. СО переводит линейный угол в равный ему линейный угол.

5. СО переводит двугранный угол в равный ему двугранный угол.

6. СО переводит ортонормированный репер R в ортонормированный репер R`. При этом точка М(x,y,z) относительно репера R переходит в точку M` с теми же координатами (x,y,z), но относительно

репера R`.

7. СО меняет ориентацию пространства

8. СО пространства можно представить в виде композиции трех зеркальных отражений.

Задачи для самостоятельного решения.

1. Какое преобразование пространства называется скользящим отражением? [6]

2. Доказать, что скользящее отражение пространства является движением.

3. Вывести формулы, задающие скользящее отражение, определяемое

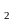координатной плоскостью Oxy и вектором a(a , a , 0) относительно прямоугольной декартовой системы координат Охуz в пространстве.

4. В какую фигуру переходит прямая (плоскость) при скользящем отражении? Обоснуйте свой ответ.

5. Что можно сказать о взаимном расположении прямой и ее образа

при скользящем отражении? Ответ обосновать.

6. Что может служить образом середины отрезка при скользящем отражении?

7. Доказать, что при скользящем отражении сохраняется простое отношение трех точек.

8. В какую фигуру при скользящем отражении преобразуется отрезок;

луч; полуплоскость? Ответ обоснуйте.

9. Что можно сказать об угле и его образе, двугранном угле и его образе при скользящем отражении?

10. Сколько инвариантных точек имеет скользящее отражение?

11. Имеет ли скользящее отражение инвариантные прямые; инвариантные плоскости? [10]

12. Составить формулы скользящего отражения, определяемого вектором

А (1, 1, - 8) и плоскостью, проходящей через точку А (1, –2, 1) и перпендикулярной прямой АВ, если В (4, 3, 2). (Система координат прямоугольная декартова).

13. Найти прообраз точки Р (2, –1, 1) при скользящем отражении, определяемом вектором а ( 2, 3, 1) и плоскостью, проходящей через точку

К (2, –1, 1) и перпендикулярной двум плоскостям 2 x - z + 1 = 0 и y = 0 . (Система координат – прямоугольная декартова).

14. Найти прообраз плоскости x + y - z = 0 при скользящем отражении,

определяемом вектором а (1, - 2, 1) и плоскостью, проходящей через точку

А(7,–5, 1) и отсекающей на осях прямоугольной декартовой системы координат равные отрезки. (Система координат – прямоугольная декартова).

15. Найти образ плоскости x + 2 y - z + 1 = 0 при скользящем отражении

пространства, определяемом вектором а (3, - 2, 2) и плоскостью, проходящей

через точку А (3, –2, –7) и параллельной плоскости 2 x -3 z + 5 = 0 . (Система

координат – прямоугольная декартова).

16. Во сколько раз увеличится объем правильной четырехугольной

призмы при скользящем отражении пространства, определяемом плоскостью,

перпендикулярной высоте призмы и проходящей через ее середину и вектором, параллельным стороне основания и имеющем длину, равную длине стороны основания?