Симметрия пространства относительно плоскости

Литература:

Таблица 55

Симметрией пространства относительно плоскости (СПОП) называется отображение пространства на себя, которое каждую точку М переводит в точку M` такую, что отрезок MM` пересекает плоскость под прямым углом и в точке их пересечения делится пополам.

Свойства:

1. СПОП переводит плоскость в плоскость, причем параллельные плоскости – в параллельные.

2. СПОП переводит прямую в прямую, причем параллельные прямые – в параллельные.

3. СПОП оставляет инвариантными плоскости, перпендикулярные плоскости симметрии, и прямые также перпендикулярные плоскости симметрии.

4. СПОП сохраняет простое отношение трех точек.

5. СПОП переводит отрезок в равный ему отрезок, луч – в луч, полуплоскость – в полуплоскость, полу-пространство – в полупространство.

6. СПОП переводит угол в равный ему угол, двугранный угол – в равный ему двугранный угол.

7СПОП переводит ортонормированный репер R в ортонормированный репер R`. При этом точка M с координатами (x,y,z) относительно репера R переходит в точку M` с теми же координатами что и точка, но только относительно репера R`.

8. СПОП меняет ориентацию пространства.

9. Композиция двух симметрий пространства относительно параллельных плоскостей является параллельным переносом на вектор перпендикулярный этим и плоскостям и имеющим длину в два раза большую расстояния между плоскостями.

Формулы симметрии пространства относительно плоскости:

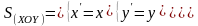
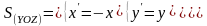
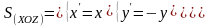
Задачи для самостоятельного решения.

1. Какое преобразование пространства называется симметрией относительно плоскости?[6]

2. Доказать, что симметрия относительно плоскости является движением.

3. Вывести формулы, задающие симметрию пространства относительно плоскости, заданной в прямоугольной декартовой системы координат

Охуz уравнением Ax + By + Cz + D = 0 .

4. В какую фигуру переходит прямая (плоскость) при симметрии пространства относительно плоскости? Обоснуйте свой ответ.

5. Что можно сказать о взаимном расположении прямой и ее образа

при симметрии пространства относительно плоскости? Ответ обосновать.

6. Что может служить образом середины отрезка при симметрии пространства относительно плоскости?

7. Доказать, что при симметрии пространства относительно плоскости

сохраняется простое отношение трех точек.

8. В какую фигуру при симметрии пространства относительно плоскости преобразуется отрезок; луч; полуплоскость? Ответ обоснуйте.

9. Что можно сказать об угле и его образе, двугранном угле и его образе при симметрии пространства относительно плоскости?

10. Имеет ли симметрия пространства относительно плоскости инвариантные прямые; инвариантные плоскости?

11. Докажите, что плоскость, делящая пополам угол между двумя плоскостями, является его плоскостью симметрии.

12. Докажите, что в тетраэдре, основанием которого служит равнобедренный треугольник, плоскость, проходящая через вершину тетраэдра и прямую, содержащую высоту равнобедренного треугольника, опущенную из его вершины на основание, является плоскостью симметрии тетраэдра.

13. Какие из элементов тетраэдра, в основании которого лежит равнобедренный треугольник, можно убрать для того, чтобы оставшаяся фигура была симметрична самой себе относительно плоскости, проходящей через вершину тетраэдра и высоту равнобедренного треугольника, опущенную из его вершины на основание?

14. Какие из элементов прямоугольного параллелепипеда можно убрать

для того чтобы оставшаяся фигура была симметрична сама себе относительно

тех же плоскостей, что и прямоугольный параллелепипед?

15. Составить формулы симметрии пространства относительно плоскости,

переводящей плоскость 3х – y + 7z – 4 = 0 в плоскость 5х + 3y – 5z + 2 = 0. (Система координат – прямоугольная декартова).

16. Составить формулы симметрии пространства относительно плоскости,

переводящей плоскость x – 2y + 3z – 4 = 0 в плоскость

x – 2y + 3z – 12 = 0. (Система координат – прямоугольная декартова).

17. Положение зеркала определяется уравнением x + y – z + 2 = 0. Найти

зеркальное изображение точки Р(1, 0, –3). (Система координат – прямоугольная декартова).

18. Найти точку, симметричную с началом координат, относительно плоскости 2х + y – z +1 = 0. (Система координат – прямоугольная декартова).

19. Найти точку, симметричную центру окружности, вписанной в треугольник с вершинами А (0, 0, 0), В(3, –2, 1), С(1, 4, 0), относительно плоскости 2x – y +5z –4 = 0. (Система координат – прямоугольная декартова).

20. Даны вершины треугольника А(4, 1, –2), В(2, 0, 0), С(–2, 3, –5). Найти

прообраз прямой, содержащей высоту треугольника, опущенную из вершины В при симметрии пространства относительно плоскости x + 2 y - 3 z + 3 = 0 . (Система координат – прямоугольная декартова).

21. В правильном треугольном диэдре SABCD центр О правильного треугольника АВС принят за начало ПДСК Охуz; направленная прямая ОА (длина отрезка ОА считается равной 1) принята за ось абсцисс; направленная прямая ОЕ, где Е – середина стороны АВ, – за ось ординат, а направленная прямая ОS – за ось аппликат. Составить формулы симметрии относительно плоскости DAC и найти координаты образа точки D(–1, –1, 1).

22. Постройте изображение куба и его образа при симметрии относительно плоскости, проходящей через концы трех ребер, исходящих из одной вер-

шины куба. Какой многогранник является пересечением этих кубов.