Поворот плоскости

Литература

Т

Поворотом плоскости (ПП) вокруг точки S на направленный угол называется такое отображение плоскости на себя, которое каждую точку М плоскости переводит в такую точку M`, что SM = SM` и направленный угол MSM` равен .

аблица 4

Свойства:

1. При ПП вокруг данной точки на заданный направленный угол прямая переходит в прямую, образующую с данной прямой направленный угол, равный углу поворота.

2. При повороте вокруг данной точки на заданный направленный угол параллельные прямые переходят в параллельные прямые.

3. ПП вокруг данной точки на заданный направленный

угол сохраняет простое отношение трех точек.

4. При ПП вокруг данной точки на заданный направленный угол отрезок переходит в равный ему отрезок, луч – в луч, полуплоскость – в полуплоскость.

5. При ПП вокруг данной точки на заданный направленный угол ортонормированный репер R переходит в ортонормированный R`.

При этом точка М с координатами х и у относительно репера R переходит в точку М` с теми же самыми координатами х и у, но относительно репера R`.

6. Композиция двух осевых симметрий плоскости с непараллельными

осями m₁ и m₂ , пересекающимися в точке О и образующими направленный угол , есть поворот плоскости вокруг точки О.

7. Всякий ПП вокруг точки О можно представить в виде композиции двух ОС, осью одной из них будет служить прямая

p, проходящая через центр О, а осью другой – прямая q, содержащая биссектрису угла, образованного образом m` луча m при повороте вокруг точки О на заданный угол и образом m`` луча m` при ОС с осью р.

Формулы поворота:

-центр поворота совпадает с началом репера R= : .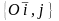

при повороте вокруг точки 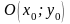 формулы имеют вид:

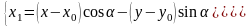
Задачи с подробным решением.

Задача 1. Постройте равносторонний треугольник так, чтобы одной его вершиной была точка Р, друга принадлежала прямой а, третья – прямой в.

Решение. Пусть 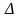РКL искомый (рис.9). Тогда точки K и L находятся на равном расстоянии от точки Р, принадлежат прямым а и в соответственно и «видны» из точки Р под углом 60⁰ (их построение обеспечивается

умением выделять на заданных фигурах соответственные при данном повороте точки). Т.к. точка L является образом точки К при повороте вокруг точки Р на 60⁰, то она принадлежит образу прямой а при указанном повороте (умение строить образы фигур при повороте), т.е. точка L есть общая точка прямой а^/=R_Р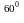 ( а) и прямой в.

Точка К является прообразом точки L. Если в= R_Р ( а), то задача имеет бесконечное множество решений.

В остальных случаях задача не имеет более двух решений, т.к. прямая в имеет не более одной точки пересечения с прямой а^/ и не более одной точки пересечения с прямой а^//= R_Р (а).

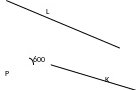
Рис. 9

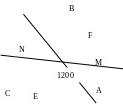
Задача 2. Через центр О треугольника АВС проведены две прямые, образующие между собой угол в 60⁰. Докажите, что отрезки этих прямых, заключенные внутри треугольника, конгруэнтны (рис.10).

Решение: Для доказательства конгруэнтности отрезков мы должны найти перемещение, при котором один из отрезков отображается на другой. Так как угол между прямыми, подмножествами которых являются указанные отрезки, равен 60⁰, то естественно рассмотреть поворот вокруг точки О. Учитывая, что поворот вокруг точки О на 120⁰ отображает треугольник на себя, приходим к целесообразности рассмотрения поворота вокруг точки О на 120⁰. При этом А В, В С, С А, АВ ВС, ВС СА, СА АВ.

Точка Е АС отобразится на точку М. Точка F АВ – на N ВС. (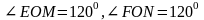 поворот сохраняет пересечение фигур). Следовательно, FE NM. Значит, FE=NM.

Рис. 10

Задача 3. Из вершины А квадрата АВСД внутрь квадрата проведены два луча, на которые опущены перпендикуляры BK,BL, ДМ, ДN из вершин В и Д. Докажите, что отрезки KL и MN равны и перпендикулярны.

Решение. Рассмотрим поворот R вокруг центра квадрата на 90⁰, при котором точки В и А перейдут соответственно в А и Д. Покажем, что при этом повороте отрезок KL перейдёт в MN. Поскольку КВА= (90⁰- КАВ)= КАД и аналогично КАВ = АДМ, луч ВК при этом перейдёт в луч АМ, а луч АК - в луч ДМ как на рисунке 11.

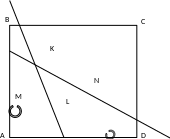
Рис. 11

Следовательно, точка К перейдёт в точку М, т.е. R (K) = M. Аналогично

R (L) = N.

Задачи для самостоятельного решения.

1. Доказать, что если некоторая фигура имеет две взаимно перпендикулярные оси симметрии, то точка их пересечения является центром симметрии этой фигуры.

2. В равнобедренном треугольнике АВС АВ = АС, ВАС = 80°. Точка О

внутри треугольника выбрана так, что ОВС = 10°, ОСВ = 30°. Найти величину угла АОВ.

3. Какое отображение плоскости на себя называется поворотом?

4. Доказать, что поворот является движением.

5. Вывести формулы, задающие поворот плоскости относительно прямоугольной декартовой системы координат Оху.

6. В какую фигуру переходит прямая при повороте плоскости вокруг точки? Ответ обоснуйте.

7. Что можно сказать об угле между прямой а и ее образом при повороте

плоскости вокруг некоторой точки на заданный угол?

8. Что можно сказать о взаимном расположении образов параллельных

прямых при повороте? Почему Вы так считаете?

9. Назовите хотя бы один поворот плоскости, при котором данная прямая

d переходит в прямую d`, образующую с d направленный угол 60°.

10. Что может служить образом середины отрезка при повороте?

11. Доказать, что при повороте сохраняется простое отношение трех точек.

12. В какую фигуру при повороте плоскости переходит отрезок; луч; полуплоскость; угол? Ответ обоснуйте.

13. Что можно сказать об образе правильного треугольника при повороте

вокруг его центра на 120°?

14. Назовите все повороты плоскости, переводящие квадрат в себя.

15. Два квадрата BCDA и BKMN имеют общую вершину В. Докажите, что медиана ВЕ треугольника АВК и высота ВF треугольника СBN лежат на одной прямой. (Вершины квадратов перечислены против часовой стрелки).

16. На сторонах ВС и CD квадрата ABCD взяты точки М и К так,

что периметр треугольника СМК равен удвоенной стороне квадрата.

Найдите величину угла МАК.

17. На сторонах АВ и АС правильного треугольника АВС выбраны точки D и E так, что AD + AE = AB. Доказать, что DC = BE, и найти величину угла DOE, где О – центр тяжести треугольника АВС.

18. Точка В лежит между точками А и С. На отрезках АВ и ВС в

одной полуплоскости с границей АС построены правильные треугольники АВЕ и ВСF. Точки М и N – середины отрезков АF и СЕ. Доказать, что треугольник ВMN правильный.

19. В правильном шестиугольнике ABCDEF точки M и N – середины сторон CD и DE, Р – точка пересечения отрезков АМ и BN.

1. Найдите угол между прямыми АМ и BN.

2. Докажите, что треугольник АВР и четырехугольник MDNP – равновелики. [7]

20. На плоскости дан отрезок АВ и точка О, не принадлежащая прямой

АВ. Построить образ отрезка АВ при повороте плоскости вокруг точки О на

направленный угол 45°.

21. На плоскости дана ломаная ABCD и точка О, не принадлежащая этой

ломаной. Построить образ ломаной ABCD при повороте вокруг точки О на направленный угол – 60°.

22. На плоскости дана окружность (О, R) с центром в точке О и радиусом

5 см. Построить образ окружности при повороте вокруг точки О на направленный угол 90°.

23. Найти образ и прообраз точки М(–2, –2) при повороте вокруг:

1) начала прямоугольной декартовой системы координат на угол 30°;

2) точки S(3, –4) на угол 60°. [6]

24. Отрезок – образ отрезка АВ при повороте вокруг точки О на угол

по часовой стрелке; М – точка пересечения отрезков АВ и А₁ В₁ . Докажите,

что: а) АМА₁ = ВМВ₁ = ;

б) точки М, О, А, А₁ лежат на одной окружности;

в) точки М, О, В, В₁ лежат на одной окружности.

25. На сторонах BC и DC квадрата ABCD взяты, соответственно, точки М

и N так, что MAN = 45°. Доказать, что AMB = AMN, AND = ANM

26. На сторонах квадрата, вне его, построены правильные шестиугольники.

Доказать, что их центры являются вершинами квадрата.

27. На сторонах ВС и CD квадрата ABCD взяты точки М и К,

соответственно, так, что ВАМ = МАК. Доказать, что ВМ + КD = АК.

28. Внутри квадрата ABCD взята точка Р. Проведены перпендикуляры: из

вершины А – к прямой ВР, из вершины В – к СР, из С – к DP, из D – к АР. Доказать, что все прямые, содержащие построенные перпендикуляры, проходят через одну точку.

29. Квадраты ABCD и AEFG на плоскости (вершины перечислены против

часовой стрелки) имеют общую вершину А. Доказать, что их центры и середины отрезков BG и DE являются вершинами некоторого квадрата.

30. Два квадрата ОАВС и 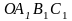(вершины перечислены в одном направлении) имеют общую вершину О. Доказать, что отрезки АА₁ и СС₁ равны и взаимно перпендикулярны. [5]

31. Через центр О правильного треугольника проведены две прямые, образующие между собой угол в 60°. Докажите, что отрезки этих прямых, заключенные внутри треугольника, равны.

32. Внутри равностороннего треугольника АВС дана точка М такая, что

АМ = 1, ВМ = 3 , СМ = 2. Найти длину стороны АВ и величины углов АМВ и ВМС.

33. Внутри равностороннего треугольника АВС дана точка М такая, что

АМ = 1, ВМ = 2 , АМВ = 105°. Найти длину отрезка СМ и величину угла

ВМС.