Движение

Литература: 1, 2, 3, 4, 5, 6, 7, 14, 20, 22, 23, 29, 31,

34, 35,40, 46, 47, 52, 53, 54, 58, 59, 60, 66, 67.

Т

Движением плоскости (пространства*) называется такое преобразование плоскости (пространства), которое сохраняет расстояние между любыми двумя точками.

аблица 1

Свойства.

1. Сохраняется соотношение

«лежать между» для точек.

2. Отрезок данный длины

отображается на отрезок той же длины.

3. Прямая отображается на параллельную ей прямую.

4. Сохраняется параллельность прямых.

5. Луч отображается на луч.

6. Угол отображается на угол той же величины.

7. Произведение двух движений есть движение;

8. Преобразование, обратное движению, есть движение.

Формулы движения:

- движение плоскости

,

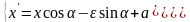- движение пространства

.

Задачи для самостоятельного решения.

1. Что такое преобразование множества?

2. Какие преобразования плоскости называются движениями?

3. Докажите, что в результате движения шар переходит в шар.

4. Докажите, что при движении угол отображается на равный ему угол.

5.Докажите, что при движении окружность отображается на окружность того же радиуса.

6. Докажите, что два параллелограмма равны, если смежные стороны и угол между ними одного параллелограмма соответственно равны смежным сторонам и углу между ними другого параллелограмма. [8]

7. Докажите, что отображение плоскости, при котором каждая точка

8. При движении прямая а отображается на прямую а₁, а плоскость , а плоскость 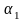. Докажите, что: а) если а|| , то а₁|| ; б) если а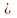 , то а₁ .

9. На координатной плоскости зададим отображение множества точек, лежащих на параболе y = x² , на множество точек, лежащих на оси Ох, следующим образом: каждой точке М параболы поставим в соответствие точку M` основание перпендикуляра, опущенного из точки М на ось абсцисс. Является ли данное отображение взаимно-однозначным? [10]

Параллельный перенос

Литература:

Таблица 2

Параллельным переносом (ПП) плоскости (пространства) на вектор 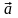называется такое отображение плоскости (пространства) на себя, при котором каждая точка М плоскости (пространства) переходит в такую точку М`, что MM` = .

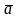Свойства:

1. ПП переводит прямую в прямую.

2. При ПП каждая прямая переходит в прямую, ей параллельную.

3. При ПП плоскости (пространства) сохраняется простое отношение трех точек.

4. ПП переводит отрезок в равный ему отрезок.

5. При ПП угол переходит в равный ему угол.

6. ПП пространства переводит плоскость в параллельную ей плоскость.

7. При ПП пространства всякая плоскость параллельная вектору a остается на месте.

8. При ПП пространства (плоскости) всякая прямая параллельная вектору a остается на месте.

9. При ПП ортонормированный репер переходит в ортонормированный репер.

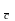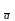10. Композиция двух ПП есть параллельный перенос, причем T o Т = T .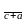

11. Множество всех ПП образует группу относительно композиции переносов.

Формулы параллельного переноса:

плоскости

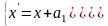
пространства

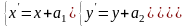
Задачи с подробным решением.

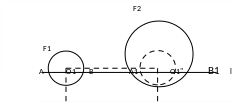
Задача 1. Даны две окружности F₁, F₂ и прямая l. Проведите прямую, параллельную прямой l , на которой окружности F₁ и F₂ высекают конгруэнтные хорды.

Решение: Пусть прямая l^/ искомая, т.е. прямая l^/ высекает на данных окружностях конгруэнтные хорды АВ и А^/В^/ (рис.1). Тогда точки А и А^/, В и В^/ можно рассматривать как соответственные при параллельном переносе: О₁ О₁^/ (умение строить соответственные точки на любых заданных фигурах). Т.к. точка А^/ является образом точки А, принадлежащей

окружности F₁, то точка А^/ принадлежит образу окружности F₁. Следовательно, А^/- общая точка окружности F₂ и образа окружности F₁ при параллельном переносе (умение строить образы фигур при параллельном переносе). Построив точку А^/, находим на окружности F₁ её прообраз (умение выделять соответственные при повороте точки на соответственных при том же повороте фигурах).

Если F₂=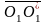 (F₁), то задача имеет бесконечное множество решений. В остальных случаях задача имеет не более четырех решений, т.к. окружность F₂ имеет не более двух точек пересечения с окружностью F₁^/= (F₁) и не более двух точек пересечения с окружностью F₁^//= (F₁).

Рис. 1

Задача 2. Расстояние между центрами двух пересекающихся окружностей равных радиусов равно d.

Прямая, параллельная линии центров, пересекает первую окружность в точках А и В, вторую – в точках С и Д. Найдите длину отрезка АС (рис.2). Решение. Обозначим центры данных окружностей через О₁и О₂.

Тогда параллельный перенос 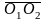(умение выделять элементы,

определяющие параллельный перенос) отобразит окружность с центром О₁ на окружность с центром О₂ (умение строить образы фигур при параллельном переносе). Точка А при этом переносе перейдёт в точку С, а точка В – в точку Д (умение видеть соответственные пи параллельном переносе точки на соответственные при том же переносе фигурах).

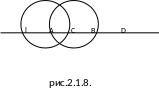Следовательно, АС=ВД= О₁О₂=d.

Рис. 2

Задача 3. Пусть a – длина большего основания трапеции, а b – длина ее меньшего основания. Доказать, что длина отрезка, соединяющего середины диагоналей, равна полуразности оснований.

Решение. В качестве вектора, определяющего параллельный перенос, в данном случае следует принять вектор ВС. При параллельном переносе, определяемом этим вектором, точка D перейдет в точку D`, при этом диагональ ВD перейдет в отрезок CD`, а середина N диагонали BD перейдет в середину N` отрезка CD`. Поскольку М– середина диагонали АС, а N` – середина отрезка CD`,

То MN` – средняя линия треугольника ACD`. Откуда следует, что длина отрезка MN` равна полусумме длин оснований трапеции ABCD. Так как отрезок MN` составлен из двух отрезков, один из которых есть искомый отрезок MN, а другой равен меньшему основанию ВС, то легко получить, что длина отрезка, соединяющего середины диагоналей, равна полуразности длин оснований трапеции.

Задача 4. Населенные пункты А и D разделены железнодорожным полотном. Где следует построить переезд ВС через полотно, чтобы путь АВСD был кратчайшим?

Решение. Границы железнодорожного полотна представляют собой две

параллельные прямые. Как известно кратчайшее расстояние между ними равно длине их общего перпендикуляра. Таким образом, отрезок ВС перпендикулярен обеим границам полотна. Следовательно, путь АВСD будет кратчайшим, если сумма расстояний АВ+CD будет наименьшей. К нахождению условий, влияющих на сумму АВ+CD , применим параллельный перенос на вектор BC. При этом точка А перейдет в точку А`. По свойству параллельного переноса АВ=A`C. А это значит, что сумма АВ+CD будет наименьшей, если наименьшей будет сумма A`C+CD. Очевидно, что эта сумма будет наименьшей в том и только в том случае, когда точки A`,C,D будут лежать на одной прямой. Итак, переезд через железнодорожное полотно должен проходить через точку С пересечения прямой A`D с границей полотна, ближайшей к населенному пункту D.

Рис. 3

Задача 5. В четырехугольнике ABCD АВ= 8, CD = 38 , ∠BAD = = 90°, ∠AВС= 120°, ∠СDА= 60°. Найти длины сторон ВС и AD.

Решение. В качестве вектора, определяющего параллельный перенос, можно взять вектор BC. При параллельном переносе, определяемом этим вектором, точка А перейдет в точку А`. Получим треугольник АА`D. В этом треугольнике можно определить угол А`AD. Его градусная мера равна 30°. В треугольнике СА`D можно найти две стороны A`C и CD и угол между ними 30°. По этим данным находим длину стороны A`D и градусную меру угла A`DС. Используя теорему косинусов, находим, что A`D = 8. А это значит, что треугольник A`DC – равнобедренный. Откуда следует, что ∠СA`D = 120°. Таким образом, мы показали, что треугольники СA`D и AA`D – равнобедренные, тупоугольные, равные между собой. Откуда следует, что AA` = 8, а AD = 38 . Так как ВС= AA`, то ВС= 8. Заметим, что треугольники АВС и АCD тоже равнобедренные. Процесс решения данной задачи позволяет сформулировать новую задачу: в четырехугольнике ABCD АВ= 8, CD = 38 , ∠BAD = 90°, ∠AВС= 120°, ∠СDА= 60°; доказать, что диагонали АС и ВD взаимно перпендикулярны.

Рис. 4

Задача 6. Найти площадь трапеции по разности оснований, равной 14 см, двум непараллельным сторонам, равным 13 и 15 см, если известно, что в трапецию можно вписать окружность.

Решение. Пусть в трапеции ABCD АВ– DC = 14, AD = 15, ВС= 13. В качестве вектора параллельного переноса возьмем вектор СD. При параллельном переносе T отрезок ВC перейдет в отрезок В`D. Рассмотрим треугольник АВ`D. По длинам сторон AD = 15, B`D = BC = 13 и AB` =14, используя формулу Герона и формулу, выражающую площадь треугольника через основание и высоту, можно найти высоту трапеции. Длина высоты трапеции равна 12 см. Для нахождения площади трапеции необходимо знать длины ее оснований. По условию около трапеции можно описать окружность. Значит, сумма боковых сторон трапеции равна сумме оснований. Так как

АВ= АВ` + CD, то AD + BC = AB` + 2DC. С учетом исходных данных можно получить, что DC = 7 см, а АВ= 21 см. Таким образом, можно вычислить площадь трапеции (168см²)

Рис. 5

Задачи для самостоятельного решения.

1. Что такое параллельный перенос?

2. Доказать, что параллельный перенос является движением.

3. Вывести формулы, задающие параллельный перенос пространства относительно системы координат Охуz.

4. В какую фигуру переходит прямая при параллельном переносе? Обоснуйте свое утверждение.

5. Что можно сказать о взаимном расположении прямой и ее образа при

параллельном переносе? Почему Вы так считаете?

6. Что может служить образом середины отрезка при параллельном переносе?

7. Изменяется ли при параллельном переносе простое отношение трех точек? Ответ обоснуйте.

8. В какую фигуру при параллельном переносе преобразуется отрезок,

луч, плоскость в пространстве? Ответ обоснуйте.

9. Что собой представляет образ двух параллельных прямых при параллельном переносе; образ пары пересекающихся прямых; образ пары скрещивающихся прямых?

10. В какую фигуру при параллельном переносе переходит параллелограмм; треугольник; трапеция?

11. В какую фигуру перейдет треугольник при параллельном переносе,

определяемом одной из медиан треугольника? Что можно сказать о расположении образов прямых, содержащих высоты треугольника по отношению к образам сторон данного треугольника?

12. Что собой представляет образ правильного треугольника при параллельном переносе, определяемом одной из сторон треугольника? Как можно определить образ центра данного треугольника?

13. Доказать, что площадь трапеции равна произведению длины

одной из непараллельных сторон и длины перпендикуляра, опущенного из

середины другой боковой стороны на первую.

14. Определить площадь треугольника, если две стороны АВ и

ВС, соответственно, равны 13 см и 15 см, а медиана ВМ, проведенная к третьей стороне, равна 6 см.

15. Найти площадь трапеции по разности оснований, равной 14

см, двум непараллельным сторонам, равным 13 и 15 см, если известно, что в

трапецию можно вписать окружность.

16. В четырехугольнике ABCD АВ = 8, CD = 8 3 , 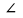BAD = = 90°,

AВС = 120°, СDА = 60°. Найти длины сторон ВС и AD.

17. В четырехугольнике ABCD продолжения сторон ВС и AD

образуют с прямой, проходящей через середины сторон АВ и CD, равные углы. Доказать, что ВС = AD.[12]

18. В основании пирамиды РАВСD лежит квадрат АВСD. Ребро РА пирамиды перпендикулярно ее основанию. Через середину ребра РВ проведено сечение, параллельное плоскости АРD. Какова площадь сечения, если площадь грани АРD равна 48?

19. Даны две пересекающиеся прямые a и b и отрезок CD. Построить

параллелограмм ABCD, вершины A и B которого лежат соответственно

на a и b. [4]

20. Доказать, что среди всех четырехугольников с заданными

диагоналями и углом между ними наименьший периметр имеет параллелограмм.

21. Дана трапеция ABCD с большим основанием АВ. Построить образ: а)

стороны АВ при параллельном переносе на вектор DC; б) образ диагонали BD

при параллельном переносе на вектор DC .

22. Построить образ окружности с центром в точке О и радиусом

R = 5 см при параллельном переносе на ненулевой вектор a .

23. Построить образ треугольника АВС при параллельном переносе на вектор AM , где М – середина стороны ВС. Какую фигуру образует треугольник

АВС со своим образом? [8]

24. Населенные пункты А и В разделены рекой с параллельными берегами и

железнодорожным полотном, расположенным параллельно берегам реки. Где

следует устроить мост через реку и переезд через железнодорожное полотно,

чтобы путь от пункта А до пункта В был кратчайшим? [6]

25. В ромбе известна длина d большей диагонали и длина a стороны. Найти площадь и высоту ромба.

26. Найти сторону ромба, если известна его площадь S и сумма m диагоналей.

27. Около окружности радиуса r описан параллелограмм, большая диагональ которого равна d. Найти площадь параллелограмма.

28. Основание равнобедренного треугольника равно 43 см, а медиана

боковой стороны – 5 см. Найти длины боковых сторон.

29. В равнобедренном треугольнике с боковой стороной, равной 4 см, проведена медиана боковой стороны. Найти основание треугольника, если медиана равна 3 см.

30. Определить площадь треугольника, если две стороны, соответственно, равны 27 см и 29 см, а медиана, проведенная к третьей стороне, равна 26 см.

31. В параллелограмме ABCD длина диагонали АС = 5, длина диагонали

BD = 7, а длина большей стороны AD параллелограмма равна 4. Найти площадь и высоту параллелограмма, проведенную к большей стороне.

32. Высота трапеции, диагонали которой взаимно перпендикулярны, равна h. Найдите площадь трапеции, если известно, что длина одной из диагоналей

равна d .

33. Диагональ равнобедренной трапеции 10 см, а площадь равна 48 см. Найти высоту трапеции.

34. Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины сторон трапеции, если площадь

равна 12 см², а длина высоты равна 2 см.

35. В равнобочной трапеции длины оснований равны 4 см и 10 см, а боковая сторона относится к высоте трапеции как 5:4. Найти площадь трапеции.

36. Большее основание трапеции имеет длину 24 см. Найти длину ее

меньшего основания, если известно, что расстояние между серединами диагоналей трапеции равно 4 см.

37. В равнобедренной трапеции одно основание равно 40 см, а другое –

24 см. Диагонали этой трапеции взаимно перпендикулярны. Найти ее площадь.

38. В равнобедренной трапеции длины оснований равны 2 см и 6 см, а дли-

на диагонали равна 5 см. Найти периметр и площадь трапеции.

39. Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины сторон трапеции, если ее площадь равна 12 см² , а длина высоты равна 2 см. [12]

40. Определить боковые стороны равнобедренной трапеции, если ее основания и площадь равны, соответственно, 8 см, 14 см и 44 см².

41. В равнобедренной трапеции боковая сторона равна средней линии, а

периметр равен 48. Найти длину боковой стороны.

42. В равнобедренной трапеции длина средней линии равна 5, а диагонали взаимно перпендикулярны. Найти площадь трапеции.

43. Площадь равнобедренной трапеции 180 см² . Длина средней линии

равна 45 см, длина боковой стороны 5 см. Найти длину меньшего основания

трапеции. [6]

44.. Высота равнобедренной трапеции равна 14 см, а основания равны 16

и 12 см. Определить площадь описанного круга.

45. Диагонали равнобедренной трапеции взаимно перпендикулярны, а ее

площадь равна a². Определить высоту трапеции.

46. Площадь равнобедренной трапеции, описанной около окружности,

равна 32 см². Найти длину боковой стороны, если угол при основании

равен 30°.

47. Основания трапеции равны 3 см и 8 см, высота равна 12 см, а одна из

боковых сторон равна 15 см. Найти другую боковую сторону трапеции.

48. В равнобедренной трапеции средняя линия равна d, а диагонали взаимно перпендикулярны. Найти площадь трапеции.

49. В каком месте следует построить мост через реку, разделяющую деревни A и B, чтобы путь между ними был кратчайшим? Берега реки—параллельные, а мост им перпендикулярен.

50. Даны две окружности и отрезок MN. Построить параллелограмм ABCD, вершины A и B которого лежат на одной окружности, вершины C и D на другой, BC =MN, BC k MN.

51. Даны две параллельные прямые и точка между ними. Построить окружность, касающуюся данных прямых и проходящую через данную точку. [5]

52. Отрезок AD точками В и С разбит на три равных отрезка. Доказать,

что для любой точки Р имеет место неравенство РА + PD ? РВ + РС.

53. Длины параллельных сторон трапеции равны 25 и 4 см, а длины непараллельных сторон – 20 и 13 см. Найти площадь и высоту трапеции.