
динамика
Динамикой называется раздел теоретической механики, в котором изучается движение тел в зависимости от действующих на них сил. Этот раздел является основным в курсе теоретической механики. Определение «теоретической» означает, что в основу разработки этого раздела положены некоторые теоретические предпосылки называемые аксиомами.
Динамика материальной точки
Аксиомы теоретической механики.
Во-первых, это три закона Ньютона:
– изолированная материальная точка движется равномерно и прямолинейно;
– ускорение,
сообщаемое точке силой, пропорционально
этой силе:
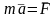 ;
;
– тела взаимодействуют между собой с силами равными по величине и направленными в противоположные стороны по одной линии.
Во-вторых, это принцип независимости действия сил: ускорения, сообщаемые точке действующими на неё силами, независимы и могут быть сложены векторно:
 . (1)
. (1)
Дифференциальные уравнения движения материальной точки.
Спроектируем равенство (1) на декартовы оси:
 (2)
(2)
Это и есть дифференциальные уравнения движения точки относительно декартовых осей координат, а если спроектировать равенство (1) на естественные оси координат:
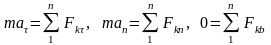
или
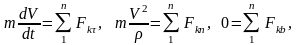 (3)
(3)
то мы будем иметь дифференциальные уравнения движения точки в естественных координатах.
Динамика механической системы
Основные закономерности движения механической системы описываются общими теоремами динамики механической системы.
Механическая система. Силы внутренние и внешние.
Механической системой называется любая совокупность материальных точек, выделенная в данной задаче. Например, группа летящих самолётов вполне может рассматриваться как механическая система. Следует заметить, что и одна материальная точка, а также твёрдое тело могут считаться разновидностями механической системы.
Если между
материальными точками существуют силы
взаимодействия, то они называются
внутренними и обозначаются
 .
.
Следует отметить, что геометрическая сумма (главный вектор) внутренних сил равна нулю ввиду того, что они действуют в механической системе попарно: как действие и противодействие.
Таким образом:

Главный момент системы внутренних сил также равен нулю в связи с тем, что внутренние силы действуют попарно по одной линии в разные стороны, следовательно, каждая пара имеет одно и то же плечо относительно любой точки. Моменты этих сил относительно любого центра будут равны по модулю, но будут иметь разные знаки.

Внешними называются
силы взаимодействия точек механической
системы с телами или точками, не входящими
в данную систему. Они обозначаются
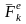 .
Геометрическая сумма этих сил называется
главным вектором внешних сил.
.
Геометрическая сумма этих сил называется
главным вектором внешних сил.

Механическая система, главный вектор внешних сил которой равен нулю, называется замкнутой.
Следует заметить, что понятие «главный вектор сил» является математической абстракцией, т.к. внешние и внутренние силы приложены к разным материальными точкам и реально сложены быть не могут.
Центр масс механической системы.
Центр масс механической системы это геометрическая точка, радиус–вектор которой определяется по формуле
 .
(7)
.
(7)
Представим эту формулу в более удобном виде:
 (8)
(8)
или, проектируя на оси координат, запишем:
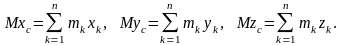 (9)
(9)
Несомненным достоинством этого понятия является полная независимость от действия любых сил или систем сил. У твердого тела, находящегося в поле сил тяжести, центр масс совпадает с его центром тяжести.
3. Дифференциальные уравнения движения механической системы.
Основное уравнение движения отдельной материальной точки может быть записано в векторной форме:
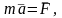 (10)
(10)
а если она в составе механической системы, то, имея в виду деление сил на внешние и внутренние:
 (11)
(11)
где
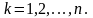
Число таких уравнений равно числу точек системы, а в проекциях на оси координат
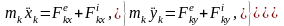 (12)
(12)
Следует заметить, что внутренние силы входят в эти уравнения в весьма сложном виде. Они зависят друг от друга, от внешних сил, от координат и скоростей всех точек системы, поэтому аналитическое решение этих дифференциальных уравнений связано зачастую с непреодолимыми трудностями. Интегрирование этих уравнений численными методами с использованием ЭВМ хотя и расширяет круг решаемых задач, однако является более примитивным методом.
В то же самое время существует вполне определенный круг задач, где совершенно необязательно решать эти задачи в полном объёме относительно каждой точки. Кроме того, связи, наложенные на точки системы, позволяют сократить число неизвестных.
В механике разработаны методы, позволяющие обойти указанные трудности решения дифференциальных уравнений движения механической системы. Это дифференциальные уравнения движения механической системы в обобщенных параметрах, принципы механики и общие теоремы динамики системы: теорема о движении центра масс, теорема об изменении количества движения, теорема об изменении кинетического момента и теорема об изменении кинетической энергии.
