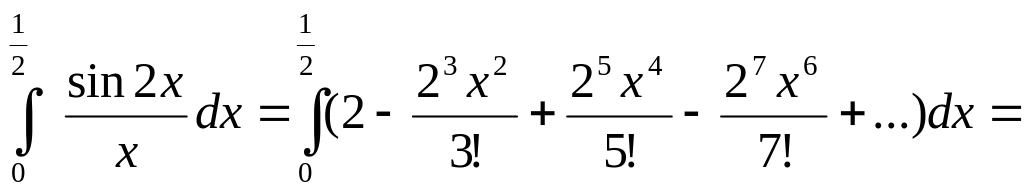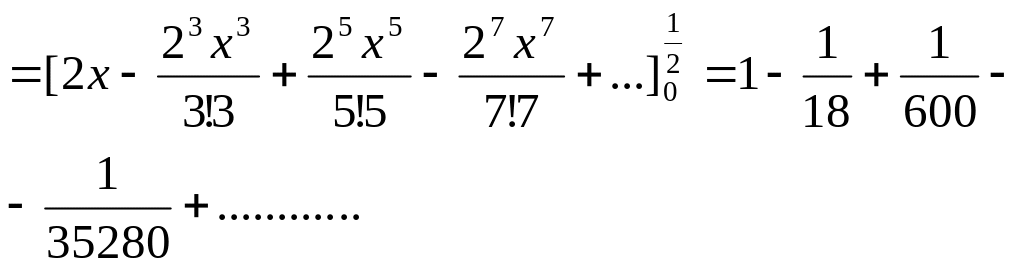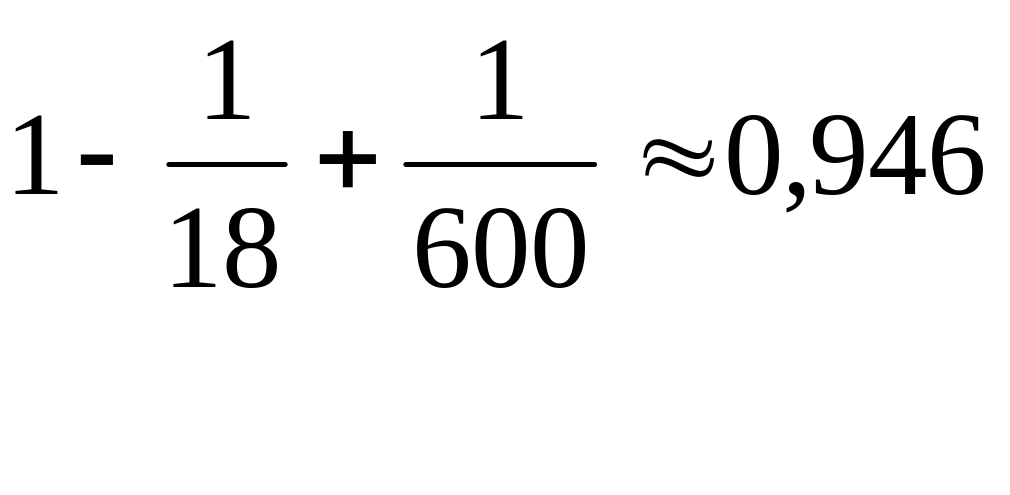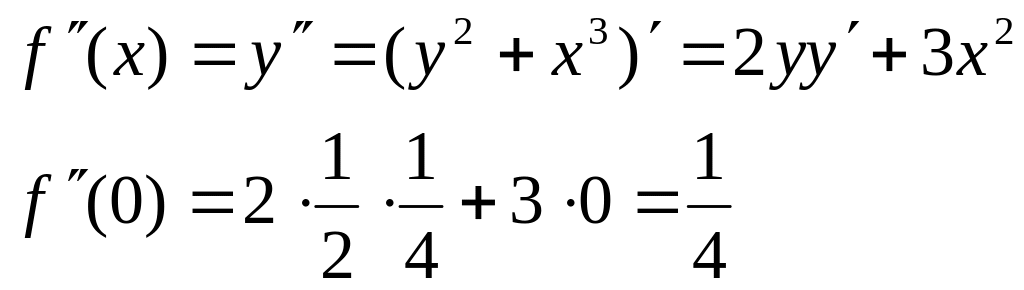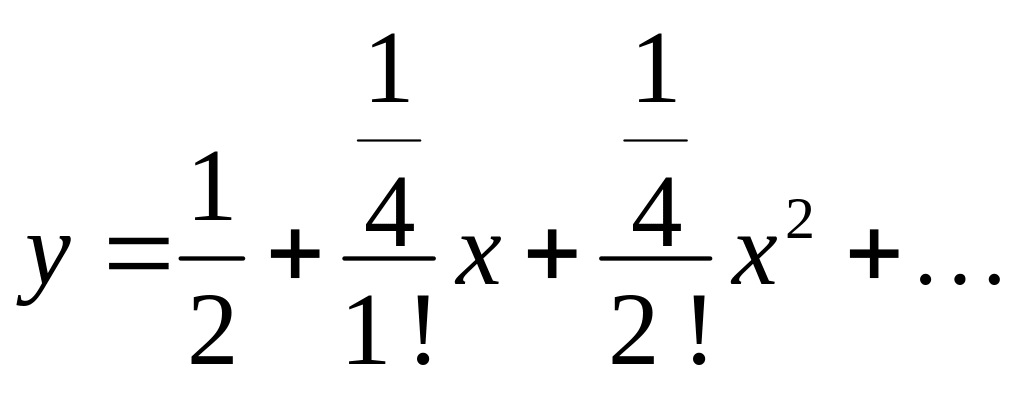- •Математика
- •Авторы : о.В. Проданец
- •Список литературы
- •§ 1. Числовой ряд. Сходимость и сумма ряда.
- •§ 2. Необходимый признак сходимости ряда.
- •§ 3. Основные свойства сходящихся рядов.
- •§ 4. Достаточные признаки сходимости,
- •§ 5. Признак сходимости Даламбера.
- •§ 6. Признаки сходимости Коши.
- •1. Интегральный признак сходимости Коши
- •2.Радикальный признак сходимости Коши.
- •§ 7. Знакочередующиеся ряды.
- •§ 8. Оценка остатка ряда.
- •§ 9. Абсолютная и условная сходимость рядов.
- •§ 10 Свойства абсолютно сходящихся рядов.
- •Глава 2 Степенные ряды.
- •§ 1. Функциональный ряд и его область сходимости. Интервал
- •§ 2 Ряды Тейлора и Маклорена.
- •Глава III Приложение степенных рядов к приближенным вычислениям
- •§1 Приближенное вычисление определенных интегралов.
- •§2 Интегрирование уравнений с помощью степенных дифференциальных рядов
- •Файл материалов Приложение № 1 Образец выполнения заданий.
§2 Интегрирование уравнений с помощью степенных дифференциальных рядов
Пусть
требуется решить дифференциальное
уравнение первого порядка
![]() при заданных начальных условиях
при заданных начальных условиях
![]() при
т.е.
при
т.е.
![]() Положим, что
Положим, что
![]() является решением данного уравнения
при указанных условиях. Искомое решение
разлагаем в ряд Тейлора в окрестности
точки
является решением данного уравнения
при указанных условиях. Искомое решение
разлагаем в ряд Тейлора в окрестности
точки
![]() :
:
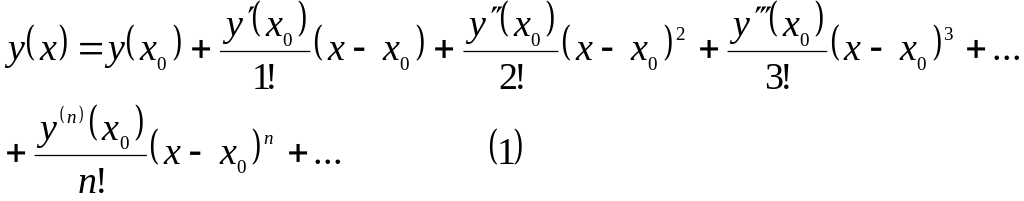
Свободный
член разложения (1), то есть
![]() ,
известен из начальных условий. Значение
,
известен из начальных условий. Значение
![]() можно получить, если подставить начальные
условия в дифференциальное уравнение.
Значение
можно получить, если подставить начальные
условия в дифференциальное уравнение.
Значение
![]() можно получить, если предварительно
продифференцировать обе части
дифференциального уравнения, а затем
подставить уже известные значения
,
можно получить, если предварительно
продифференцировать обе части
дифференциального уравнения, а затем
подставить уже известные значения
,
![]() Поступая аналогично, т.е.
Поступая аналогично, т.е.
последовательно
дифференцируя обе части заданного
уравнения по переменной х, можно
последовательно находить значения
![]() и т.д.
и т.д.
Пример.
Найти частное решение
дифференциального уравнения
![]() соответствующее начальным условиям
соответствующее начальным условиям
![]()
Решение.
Так
как по условию
![]() то искомое частное решение
можно записать так:
то искомое частное решение
можно записать так:
![]()
Свободный
член
![]() по условию. Значение
по условию. Значение
![]() находим, подставляя в заданное уравнение
начальные условия:
находим, подставляя в заданное уравнение
начальные условия:
![]()
Последовательно
дифференцируя данное дифференциальное
уравнение, находим
![]() и т.д. и затем вычисляем значения
производных при х=0.
и т.д. и затем вычисляем значения
производных при х=0.
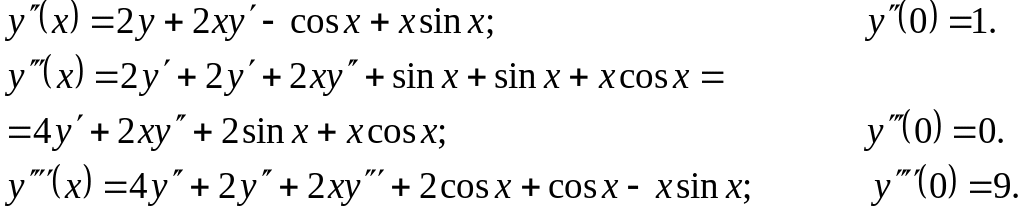
Подставив найденные значения производных при х=0, получим первые члены разложения в степенной ряд искомого частного решения:
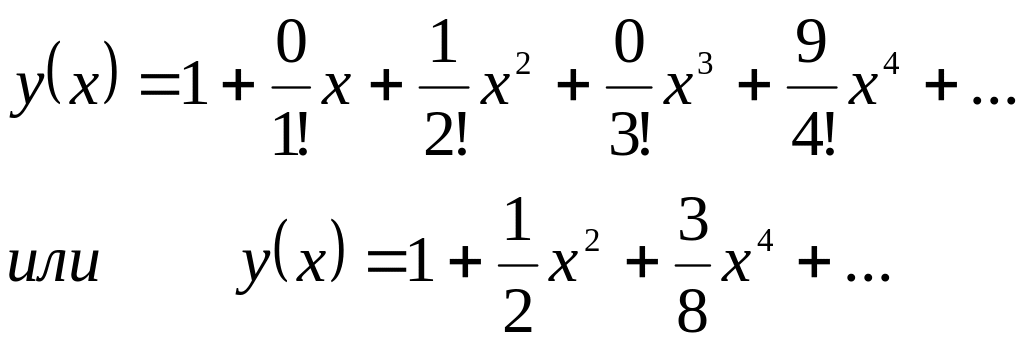
Файл материалов Приложение № 1 Образец выполнения заданий.
Задача 1.
Исследовать на сходимость следующий числовой ряд.
Пример
1.

Применяем
признак Даламбера. Здесь
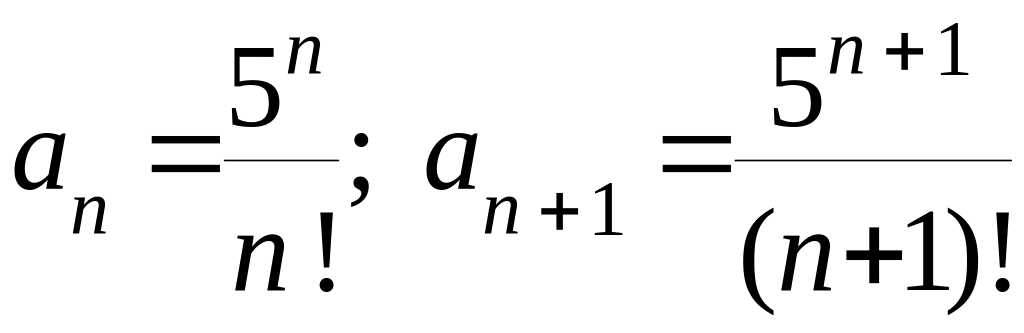
Вычислим число

Получили
![]() следовательно, ряд сходится.
следовательно, ряд сходится.
Пример
2.
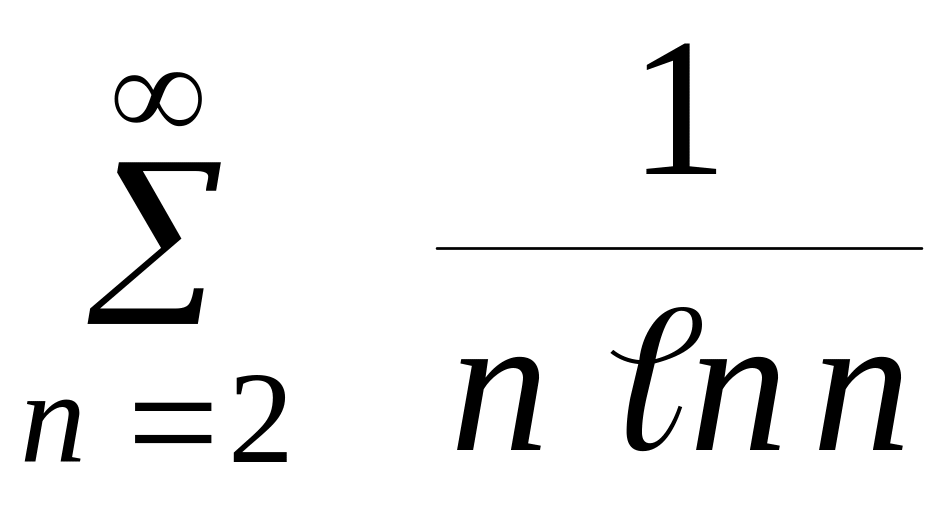
Применим
интегральный признак Коши. Составим
несобственный интеграл. Так как
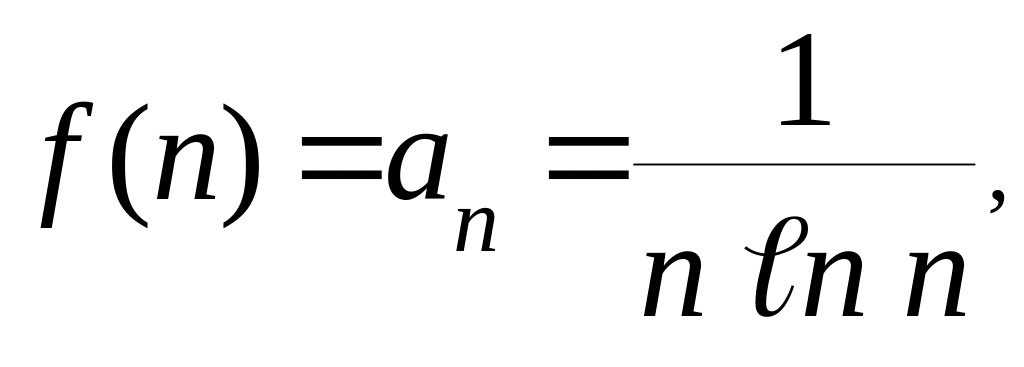 то функцией, принимающей в точках
то функцией, принимающей в точках
![]() значения
значения
![]() будет функция
будет функция
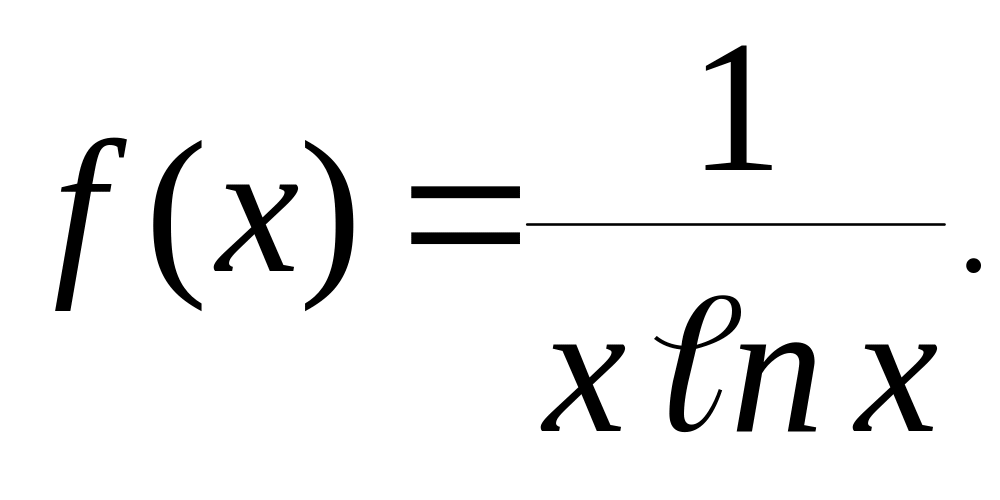 Она непрерывна в промежутке
Она непрерывна в промежутке
![]() и монотонно в нем убывает.
и монотонно в нем убывает.
Вычислим
несобственный интеграл
![]()

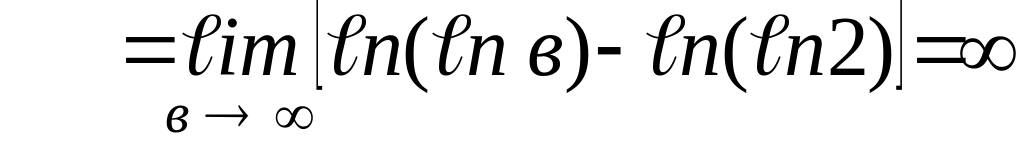
Интеграл
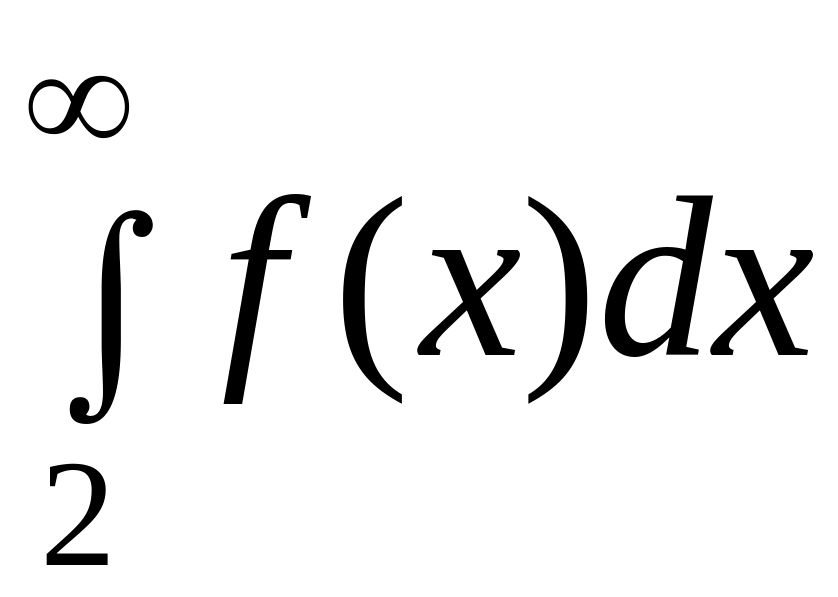 расходится. Из его расходимости следует
расходимость
данного
ряда.
расходится. Из его расходимости следует
расходимость
данного
ряда.
Пример
3.
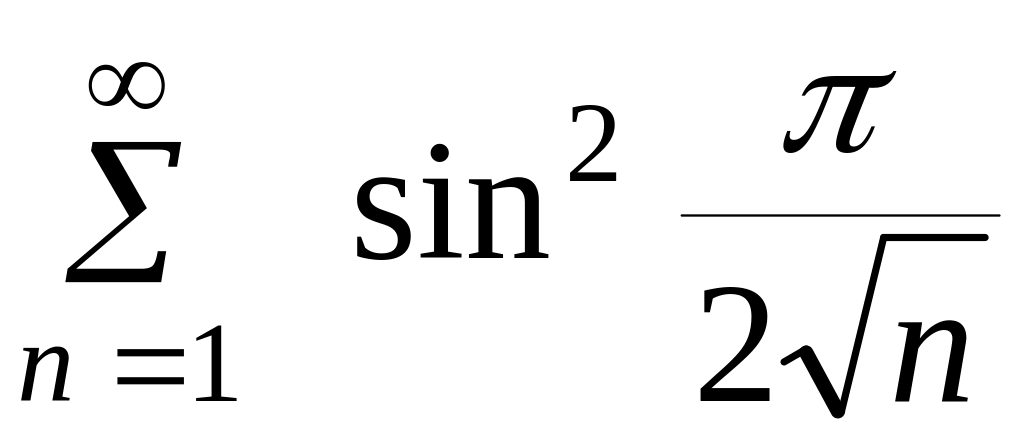
Установим
эквивалентность последовательностей
при
![]()
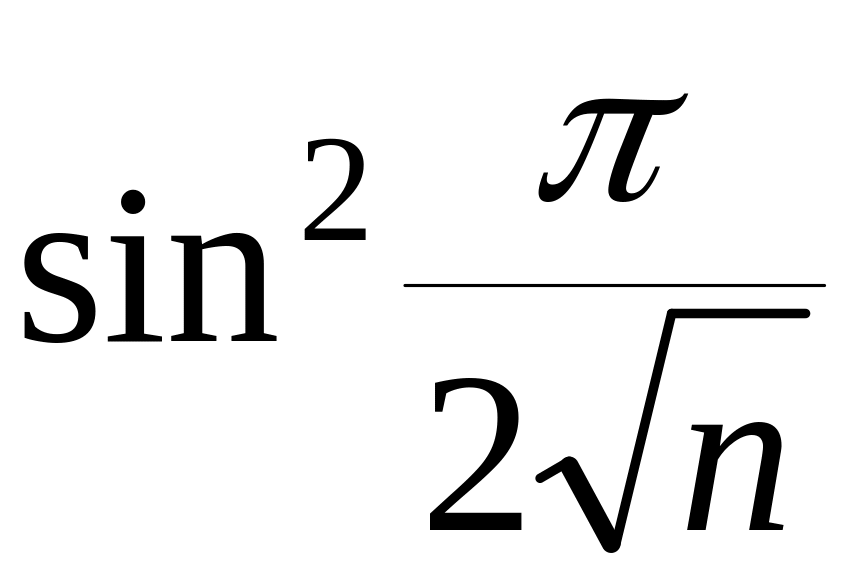 ~
~
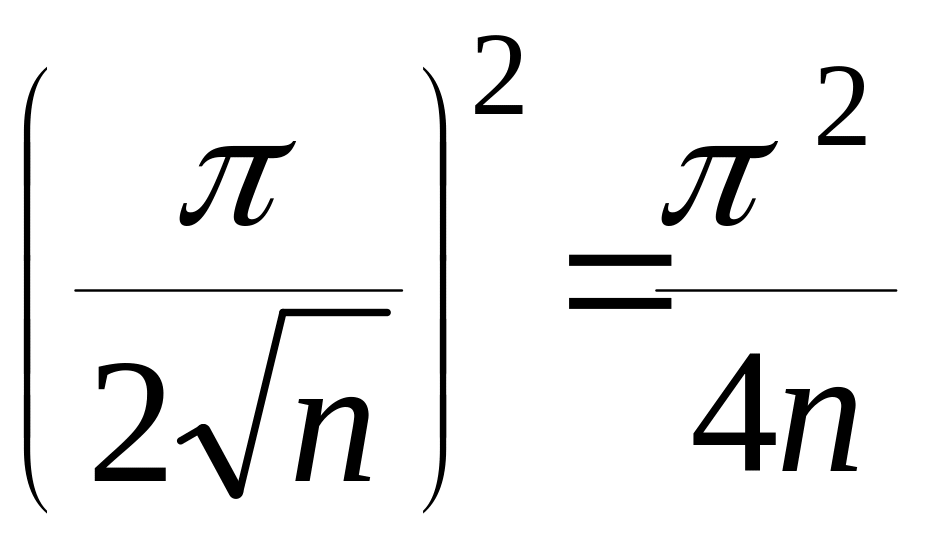
Значит, данный ряд ведет себя (в смысле сходимости) так же, как ряд
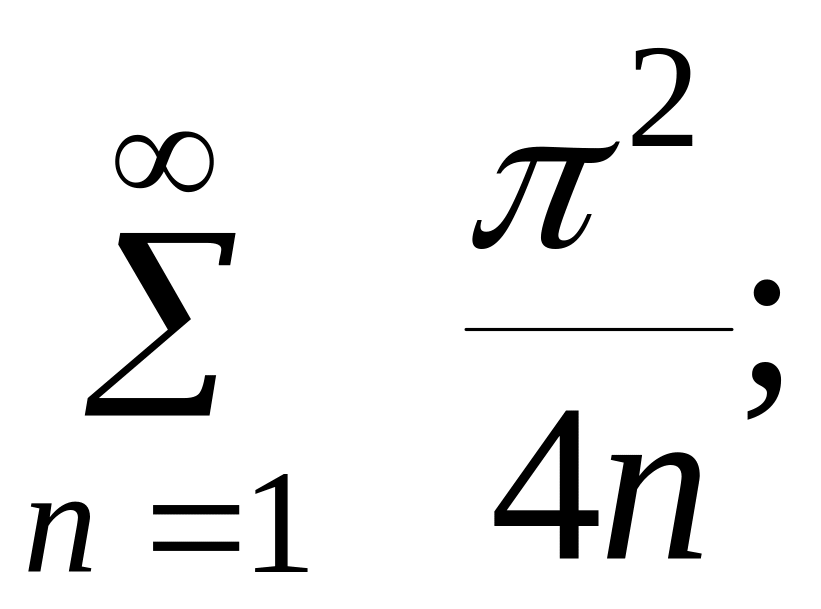
Но
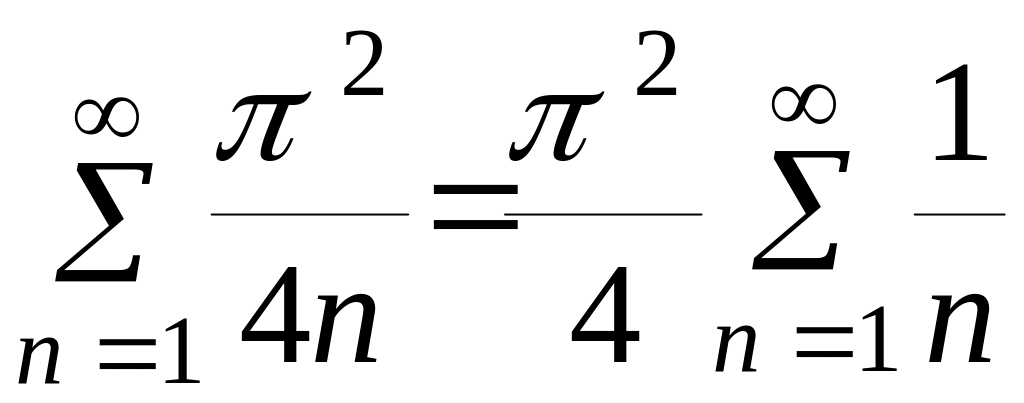 - ряд расходится как
- ряд расходится как
гармонический ряд.
Следовательно, данный ряд расходится.
Задача 2.
Найти интервал сходимости степенного ряда:
Пример
1.
Применим
признак Даламбера. Выпишем:
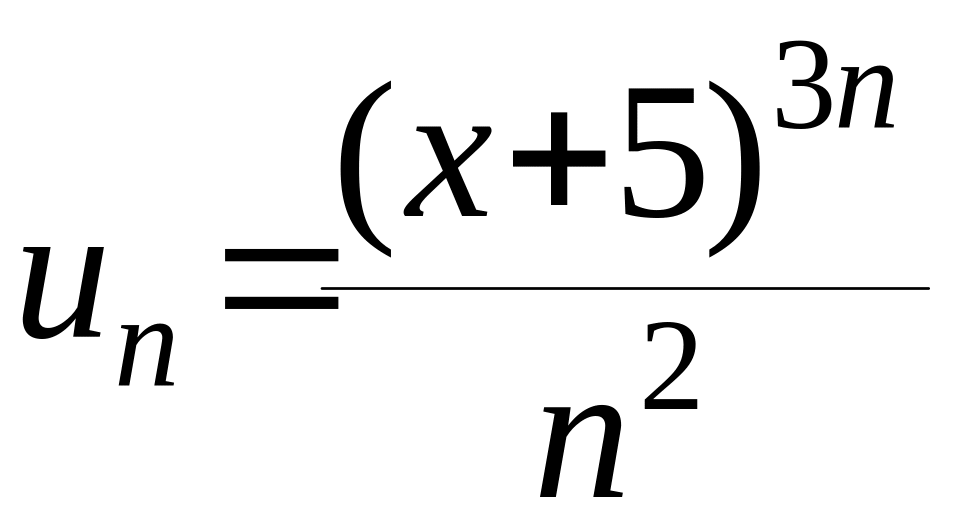 ,
тогда
,
тогда
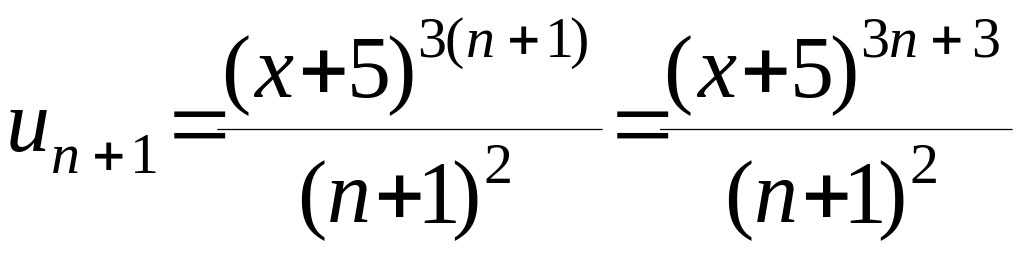 .
.
Найдем предел
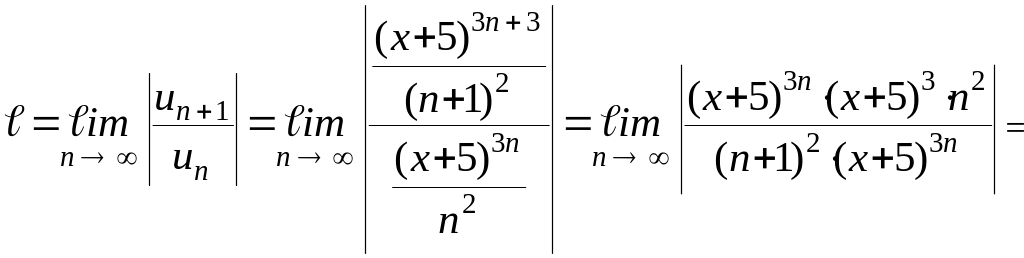
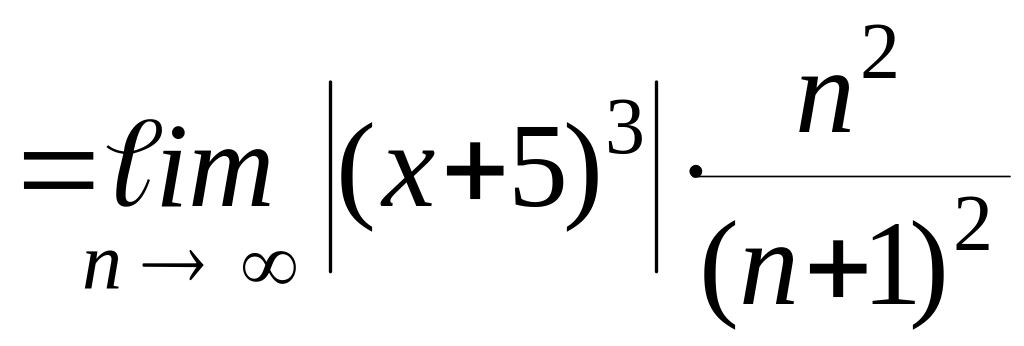
![]() .
.
Определим,
при каком значении
![]() этот предел будет меньше единицы.
этот предел будет меньше единицы.
![]()
Границы найденного интервала исследуем отдельно.
При
![]() получим числовой знакочередующийся
ряд
получим числовой знакочередующийся
ряд
![]()
Применим признак Лейбница:
1)
u1>u2
>u3 >…>
u4 >…
1)
![]()
2)
![]() 2)
2)
![]()
Ряд
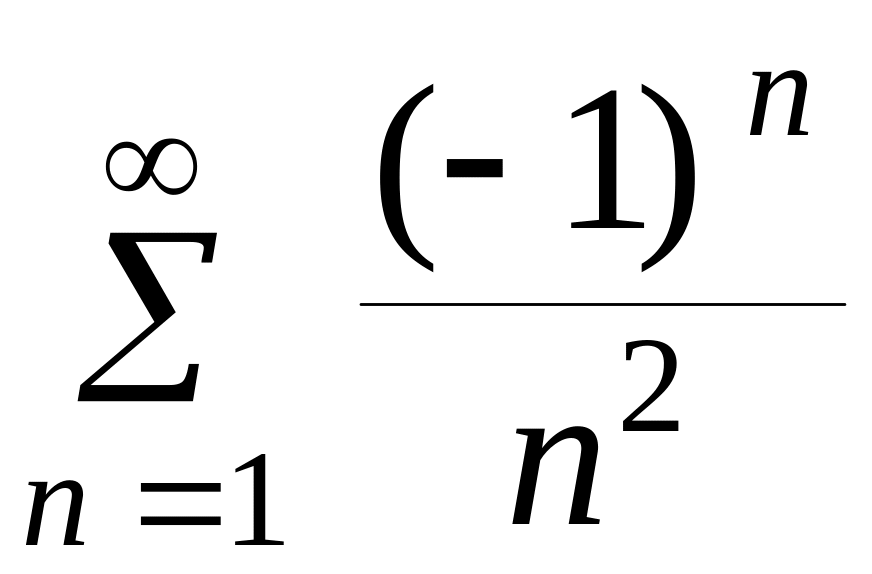 сходится по признаку Лейбница. Причем
он сходится абсолютно, т.к. ряд, составленный
из абсолютных величин его членов,
сходится.
сходится по признаку Лейбница. Причем
он сходится абсолютно, т.к. ряд, составленный
из абсолютных величин его членов,
сходится.
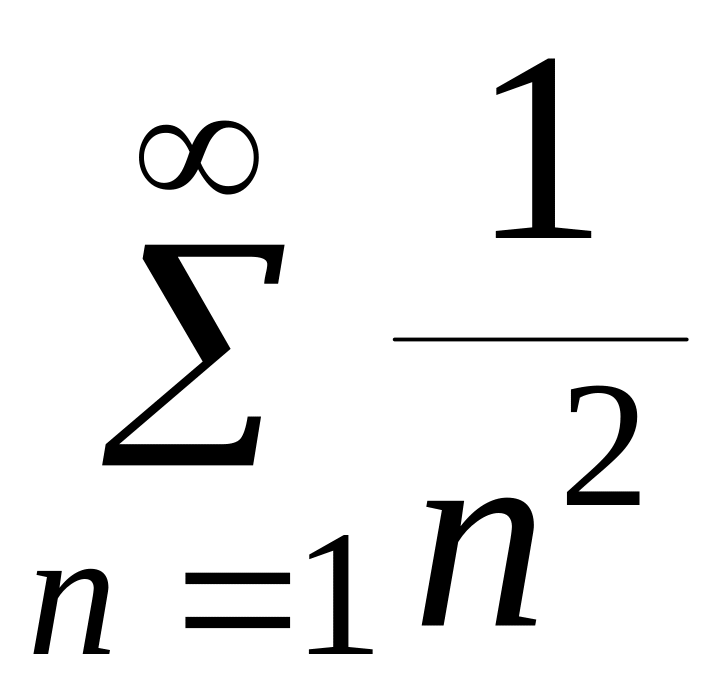 - сходится как
обобщенный гармонический ряд, у которого
- сходится как
обобщенный гармонический ряд, у которого
р = 2.
При х = -4 получим числовой знакоположительный ряд:
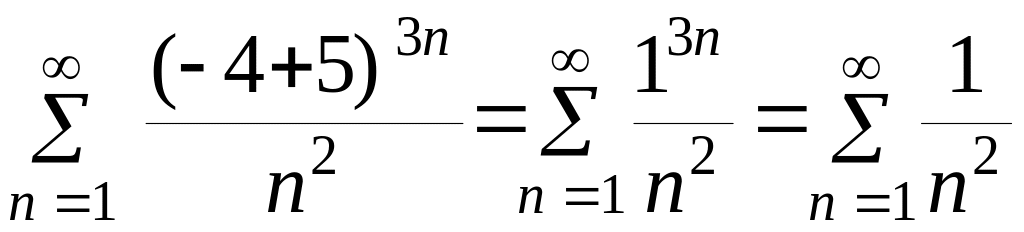 ,
,
который является сходящимся рядом.
Следовательно, интервалом сходимости ряда является отрезок
![]()
Пример 2.
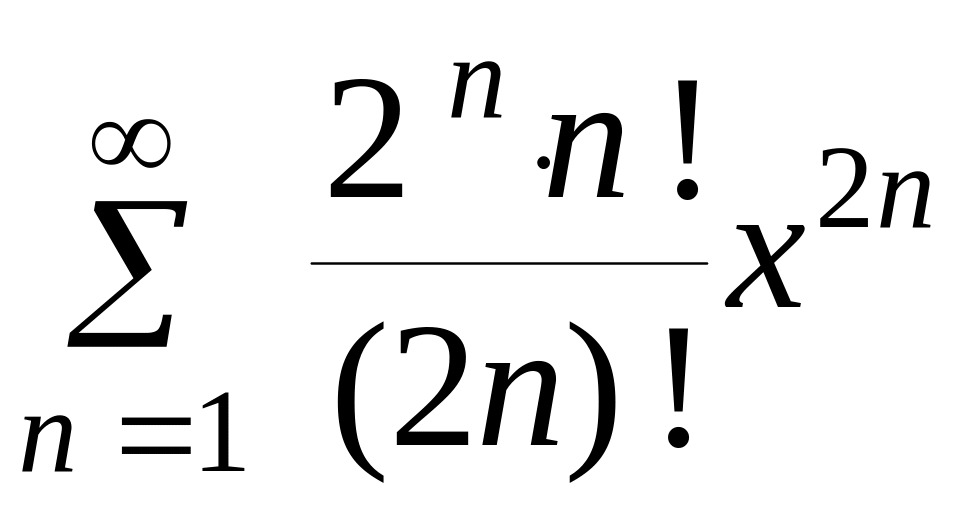
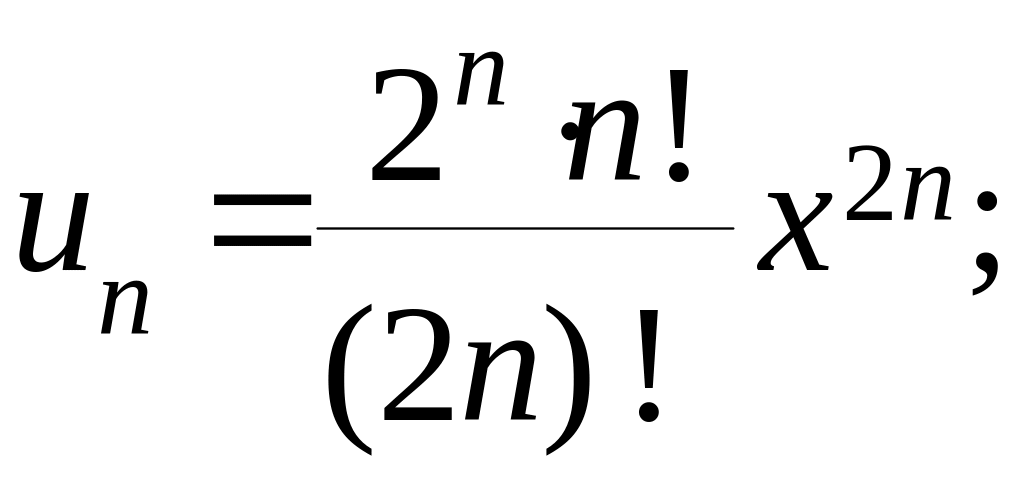
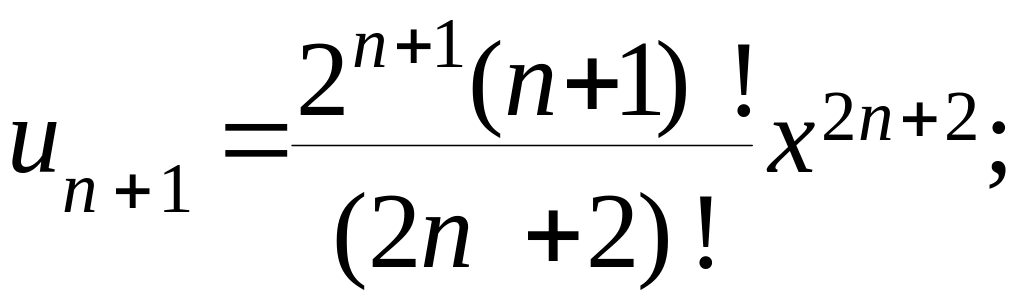
![]()
![]()
![]()
![]()
![]()
![]() .
.
Для
данного ряда
![]() < 1 при любом
х
.
< 1 при любом
х
.
Следовательно,
этот ряд сходится при любом значении
х и
его интервал сходимости – вся числовая
ось
![]() .
.
Задача 3.
Вычислить
определенный интеграл
![]() с
точностью до 0,001, разложив подынтегральную
функцию в ряд и затем проинтегрировав
его почленно.
с
точностью до 0,001, разложив подынтегральную
функцию в ряд и затем проинтегрировав
его почленно.
Разложим подынтегральную функцию в биномиальный ряд:
![]()
полагая
t
= x3,
m
=
![]()
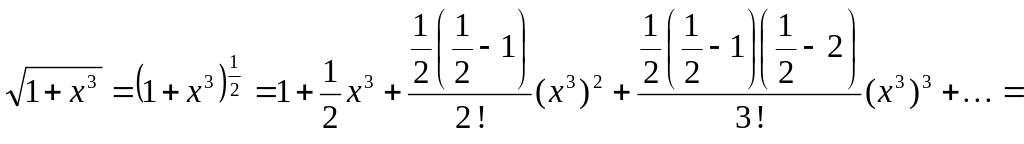
![]()
Интегрируем:
![]()
![]()
![]()
Вычислили несколько последовательных первых членов полученного знакочередующегося сходящегося ряда с (с одним лишним знаком).
Согласно
свойству знакочередующегося сходящегося
ряда, для вычисления интеграла с точностью
до 0,001 достаточно взять сумму двух первых
членов ряда. Ошибка вычисления меньше
абсолютного значения первого из
отброшенных членов ряда, т.е. меньше
![]()
Значит,
![]()
Ответ округляем до 0,001.
Ответ:
![]()
Задача 4.
Найти
три первых отличных от нуля члена
разложения в степенной ряд решения
![]() дифференциального уравнения
дифференциального уравнения
![]()
![]() удовлетворяющего
начальному условию
удовлетворяющего
начальному условию
![]()
Решение дифференциального уравнения ищем в виде степенного ряда
![]()
По
условию,
![]()
Вычислим
![]()
т.е.
![]() .
.
Найдем
вторую производную
![]()
![]()
![]()
![]() т.е.
т.е.
![]()
Представляем найденные значения производных в искомый ряд
![]()
Ответ:
![]()
Приложение № 2
Часто применяемые для сравнения ряды:
1)
1+![]() -гармонический ряд. Он расходится.
-гармонический ряд. Он расходится.
1+
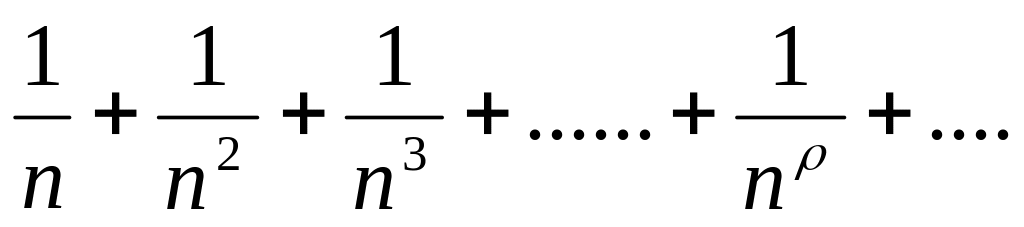 =
=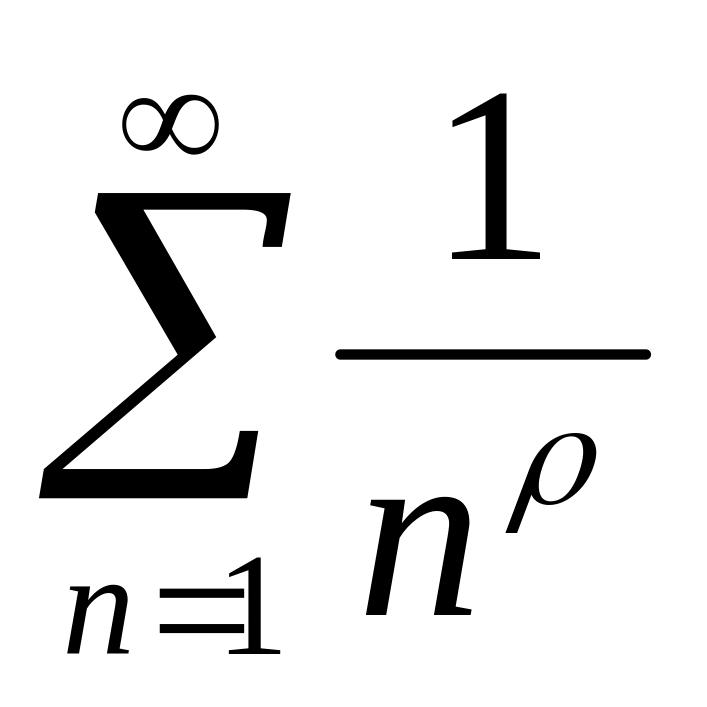 -
обобщенный гармонический ряд:
-
обобщенный гармонический ряд:
р![]() 1-
ряд расходится,
1-
ряд расходится,
р >1- ряд сходится.
3) 1+ q+ q2 +q3 +……+qn-1+qn+….-геометрическая прогрессия,
![]() <1-ряд
сходится,
<1-ряд
сходится,
>1-ряд pасходится,
q=1,q=-1- ряд расходится.
Приложение № 3
Разложение в степенной ряд некоторых функций:
![]()
![]()
sin
x =![]()
cos
x =![]() n
n![]()
ln(1+x)=
![]() -1<x<1
-1<x<1
arctg
x =![]() -1
-1![]() 1
1
(1+x)m=![]() -1<x<1
-1<x<1
![]() -1<x<1
-1<x<1
Перечень умений
№ |
Умение |
Алгоритмы |
1 |
Исследовать на сходимость ряд |
1. Написать формулу общего члена ряда; 2. Определить: знакоположительный ряд или знакопеременный ряд; 3. Если ряд знакоположительный, то по виду общего члена выбирают один из признаков сходимости рядов: а) необходимый признак сходимости; б) признаки сравнения рядов; в) признак Даламбера; г) признаки сходимости Коши. 4. Если ряд знакопеременный, то а) Если ряд знакочередующий то проверяем условия применения признака Лейбница: - ряд монотонно убывает по абсолютной величине; - б) иначе составляем ряд из соответствующих абсолютных величин членов ряда и определяем его сходимость по одному из перечисленных признаков сходимости знакоположительных рядов; в) определяем или абсолютную или условную сходимость ряда. 5. Определить сходимость ряда. |
2 |
Найти интервал сходимости ряда |
1. Выписать un и найти un+1. 2.
Найти предел :
3. Определить при каком значении х этот предел будет меньше единицы. 4. Исследовать границы найденного интервала. 5. Выписать интервал сходимости ряда. |
3 |
Найти приближенное значение определенного интеграла с задан ной точностью |
1.Представить подынтегральную функцию в виде степенного ряда. 2.Интегрировать почленно полученный ряд в указанных пределах. 3. Определить какой член ряда по абсолютному значению меньше заданной точности. 4. Найти сумму первых членов ряда до определенного выше члена. 5. Записать ответ, выписав значение. |
4 |
Найти частное решение дифференциального уравнения |
1.Представить
решение дифференциального уравнения
в виде степенного ряда:
2.Из
начальных условий определяем
коэффициенты
3.
Последовательно дифференцируем
уравнение и определяем
4. Подставляем найденные значения производных в искомый ряд. 5. Выписать ответ. |
Перечень знаний
Контрольные вопросы для самопроверки.
1.Что называется числовым рядом? Общим членом ряда?
2.Что называется n-ой частичной суммой ряда? суммой ряда?
3.Какой ряд называется сходящимся ? расходящимся ?
4.В чем состоит необходимый признак сходимости ряда?
5.Какой ряд называется гармоническим? Выполняется ли для
него необходимый признак сходимости ряда? Сходится ли
гармонический ряд?
6.Сформулируйте достаточные признаки сходимости ,
основанные на сравнении рядов с положительными членами.
7.Сформулируйте признак сходимости Даламбера.
8. В чем состоит интегральный и радикальный
признаки сходимости ряда Коши?
9.Какой ряд называется знакочередующим? Сформулируйте
признак Лейбница о сходимости знакочередующего ряда.
10. Какой ряд называется абсолютно сходящимся ? Условно
сходящимся ?
11. Какой ряд называется функциональным?
12.Что называется областью сходимости функционального ряда?
Какой ряд называется степенным?
14.Сформулируйте теорему Абеля о сходимости степенного ряда.
15.Как найти интервал(область) сходимости степенного ряда?
16.Сформулируйте теоремы о почленном дифференцировании
и интегрировании степенных рядов.
17.Какой степенной ряд называется рядом Тейлора
данной функции?
18.Напишите формулу остаточного члена ряда Тейлора.
19.Какой степенной ряд называют рядом Маклорена?
20.Напишите разложения в степенной ряд функций
![]() и
укажите
и
укажите
их область сходимости.
21.Изложите сущность приближенного вычисления
определенных интегралов.
22.Изложите сущность интегрирования дифферециальных уравнений с помощью степенных рядов.
Тренинг умений
Примеры выполнения упражнений тренинга на умение №1
Задание №1а
Исследовать сходимость ряда :
![]()
Решение.
Заполните таблицу, подобрав каждому алгоритму конкретное содержание.
№ п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму
|
1 |
Написать формулу общего члена ряда
|
un= |
2 |
Определить знаки ряда |
Ряд знакоположительный
|
3 |
Выбрать признак сходимости ряда |
Применяем признак Коши:
|
4 |
Определить сходимость ряда |
0<1-ряд сходится |
Задание №1в
Исследовать сходимость ряда :
![]()
Решение
Заполните таблицу, подобрав каждому алгоритму конкретное содержание.
№ п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму |
1 |
Написать формулу общего члена ряда
|
un=(-1)n-1 |
2 |
Определить знаки ряда |
Ряд знакочередующий |
3 |
Выбрать признак сходимости ряда |
Данный ряд удовлетворяет условиям признака Лейбница: 1)члены ряда по абсолютной величине монотонно убывают, т.е.
2) |
4 |
Определить сходимость ряда |
Ряд расходится |
Задание №1с
Доказать, что ряд сходится абсолютно:
![]()
Решение
Заполните таблицу, подобрав каждому алгоритму конкретное содержание.
№ п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму |
1 |
Написать формулу общего члена ряда |
Ряд произвольного знака |
2 |
Определить знаки ряда |
Ряд знакопеременный
|
3 |
составляем ряд из соответствую- щих абсолютных величин членов ряда |
получили
бесконечно убывающую геометрическую
прогрессию, q= |
4 |
Определяем абсолютную или условную сходимость ряда |
Данный ряд абсолютно сходящийся |
Решите самостоятельно:
Исследовать сходимость ряда:
1)![]()
2)![]()
3)
![]()
4)![]()
5)![]()
6)![]()
Исследовать на сходимость и абсолютную сходимость ряды:
1)
![]()
2)
![]()
![]()
3)
![]()
4)
![]()
Задание № 2
Найти интервал сходимости ряда:
![]()
Решение
Заполните таблицу, подобрав каждому алгоритму конкретное содержание.
№п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму |
1 |
Выписать un и найти un+1
|
un= |
2 |
Найти предел :
|
|
3 |
Определить при каком значении х этот предел будет меньше единицы
|
|
4 |
Исследовать границы найденного интервала |
Если
х=1, то получаем
гармонический ряд, он расходится, Если
х=-1, то получаем
Этот ряд сходится по признаку Лейбница
|
5 |
Выписать интервал сходимости ряда
|
-1 |
Решите самостоятельно:
Найти интервал сходимости ряда:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
Задание № 3
Вычислить определенный интеграл
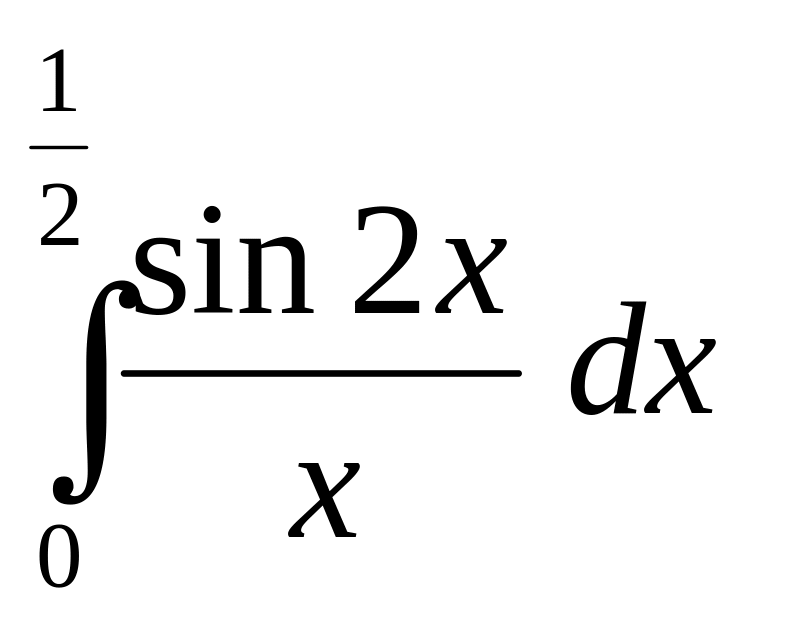 с
точностью
до
0,001
с
точностью
до
0,001
Решение
Заполните таблицу, подобрав каждому алгоритму конкретное содержание.
№п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму |
1 |
Представить подынтегральную функцию в виде степенного ряда. |
Заменить в разложении sin x, x на 2х, Получим:
тогда
|
2 |
Интегрировать почленно полученный ряд в указанных пределах
|
|
3 |
Определить какой член ряда по абсолютному значению меньше заданной точности
|
|
4 |
Найти сумму первых членов ряда до определенного выше члена
|
|
5 |
Записать ответ, выписав значение |
|
Решите самостоятельно:
Вычислить определенный интеграл с точностью до 0,001:
1)![]()
2)

3)

4)

5)

Задание № 4
Найти три первых
отличных от нуля члена разложения в
степенной ряд решения
дифференциального уравнения
![]() удовлетворяющего начальному условию:
удовлетворяющего начальному условию:
![]()
Решение
Заполните таблицу, подобрав каждому алгоритму конкретное содержание.
№п/п |
Алгоритмы |
Конкретное соответствие задания заданному алгоритму
|
|
1 |
Представить решение дифференциального уравнения в виде степенного ряда |
Так как х=0,то
|
|
2 |
Из
начальных условий определяем
коэффициенты
|
вычислим т.е.
|
|
3 |
Последовательно дифференцируем уравнение и определяем
|
Найдем вторую производную
|
|
4 |
Подставляем найденные значения производных в искомый ряд. |
|
|
5 |
Выписать ответ |
|
|
Решите самостоятельно:
Найти
три первых отличных от нуля члена
разложения в степенной ряд решения
дифференциального уравнения
![]()
удовлетворяющего
начальному условию
![]()
1)![]()
2)![]()
3)
![]()
4
![]()
5)![]()
Cамостоятельная работа
Задача 1.
Исследовать на сходимость следующий числовой ряд:
Задача 2.
Найти интервал сходимости степенного ряда
Задача 3.
Вычислить определенный интеграл
![]()
с точностью до 0,001 , разложив подынтегральную
функцию в ряд
и затем проинтегрировав его почленно
3.1
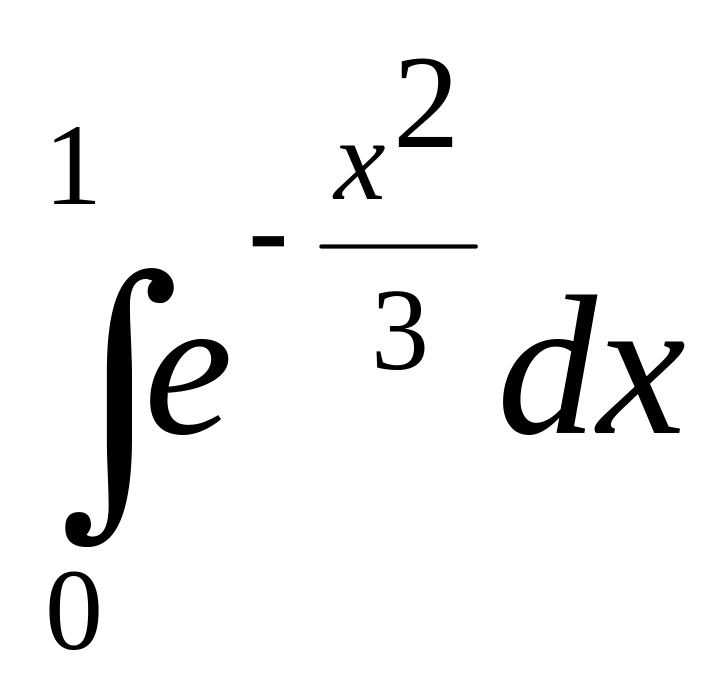 3.9
3.9
![]()
3.2
![]() 3.10
3.10
![]()
3.3
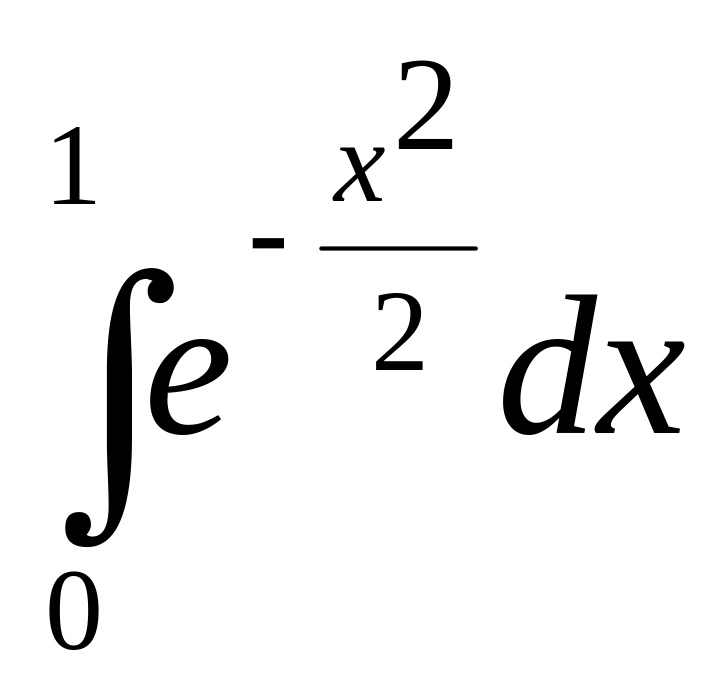 3.11
3.11![]()
3.4
![]() 3.12
3.12
![]()
3.5
![]() 3.13
3.13
![]()
3.6
![]() 3.14
3.14
![]()
3.7
![]() 3.15
3.15
![]()
3.8
![]() 3.16
3.16
![]()
3.17
![]() 3.19
3.19
![]()
3.18
![]() 3.20
3.20
![]()
Задача 4.
Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения удовлетворяющего начальному условию
4.1
![]() 4.9
4.9
![]()
4.2
![]() 4.10
4.10
![]()
4.3
![]() 4.11
4.11
![]()
4.4
![]() 4.12
4.12
![]()
4.5
![]() 4.13
4.13
![]()
4.6
![]() 4.14
4.14
![]()
4.7
![]() 4.15
4.15
![]()
4.8
![]() 4.16
4.16
![]()
4.17
![]() 4.19
4.19
![]()
4.18
![]() 4.20
4.20
![]()
Глоссарий
№ п/п |
Новые понятия |
Содержение |
1 |
Числовой ряд |
Бесконечная числовая последовательность
: u1+u2+u3+…+un+un+1+…
(1)
или
|
2 |
Частичная сумма ряда Sn |
Сумма первых n членов ряда (1) |
3 |
Ряд сходится |
Если
|
4 |
Ряд расходится |
Если
частичная сумма Sn
не имеет
|
5 |
Необходимый признак сходимости ряда |
Ряд
(1) сходится если существует
|
6 |
Достаточные признаки сходимости рядов: 1.Признак сравнения 1
2.Признак сходимости 2
3.Признак Даламбера
4.Радикальный признак Коши
5.Интегральный признак Коши |
Если каждый член ряда (1) начиная с некоторого члена не превосходит соответствуюшего члена другого заведомо сходящегося ряда V1+v2+…….+vn.+…….. (2) То данный ряд (1) тоже сходится. Если для ряда(1) существует ряд (2) такой, что ,то рассматриваемые ряды либо оба сходятся, либо оба расходятся. Если
для ряда (1)
а) q<1, то ряд (1) сходится б) q>1, то ряд (1) расходится в) q=1, используем другой признак Если
для ряда (1)
а) q<1, то ряд (1) сходится б) q>1, то ряд (1) расходится в) q=1, используем другой признак Если функция f(х) на промежутке [1,+ ) является непрерывной, положительной и монотонно убывающей, то ряд (1), где un=f(х), сходится, если сходится несобственный интеграл
|
7 |
Знакопеременный Ряд |
Ряд, среди членов которого имеются как положительные, так и отрицательные члены (притом и тех и других неограниченное число) |
8 |
Знакочередующийся ряд
|
Знакопеременный ряд –ряд, у которого любые два рядом стоящие члена имеют противоположные знаки. Знакочередующийся ряд можно записать так: (3) где все числа (n=1,2,3…) положительны. |
9 |
Признак Лейбница |
Если члены ряда (3) монотонно убывают по абсолютной величине и общий член стремится к нулю при т.е.
|
10 |
Абсолютно сходящийся ряд |
ряд с членами произвольного знака (4) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов, то есть сходится ряд (5). (5) |
11 |
условно сходящийся ряд |
Ряд (4) называется условно сходящимся, если он сходится, но ряд, составленный из абсолютных величин его членов, то есть ряд (5), расходится |
12 |
Функциональ- ный ряд |
Ряд вида: (6) |
13 |
Область сходимости функционального ряда |
совокупность всех значений аргумента х, при которых ряд (6) сходится
|
14 |
степенной ряд |
Ряд вида:
|
15 |
Теорема Абеля |
Если степенной ряд (7) сходится при то он сходится абсолютно
при любом значении х, удовлетворяющем
неравенству
Если же степенной ряд (7) расходится при то он расходится при любом значении х, удовлетворяющем неравенству |
16 |
Радиус сходимости рядов |
-R<X<R, где
радиус сходимости R= Отметим, что формула (8) справедлива только в том случае, если степень х при переходе от одного члена к следующему возрастает строго на единицу. |
17 |
Свойства степенных рядов |
Теорема 1. Сходящийся степенной ряд можно почленно дифференцировать любое число раз внутри его области сходимости. Теорема 2. Сходящийся степенной ряд можно почленно интегрировать в любом промежутке, содержащемся внутри области сходимости данного ряда. |
18 |
Ряд Тейлора |
|
19 |
Ряд Маклорена
|
Ряд:
|

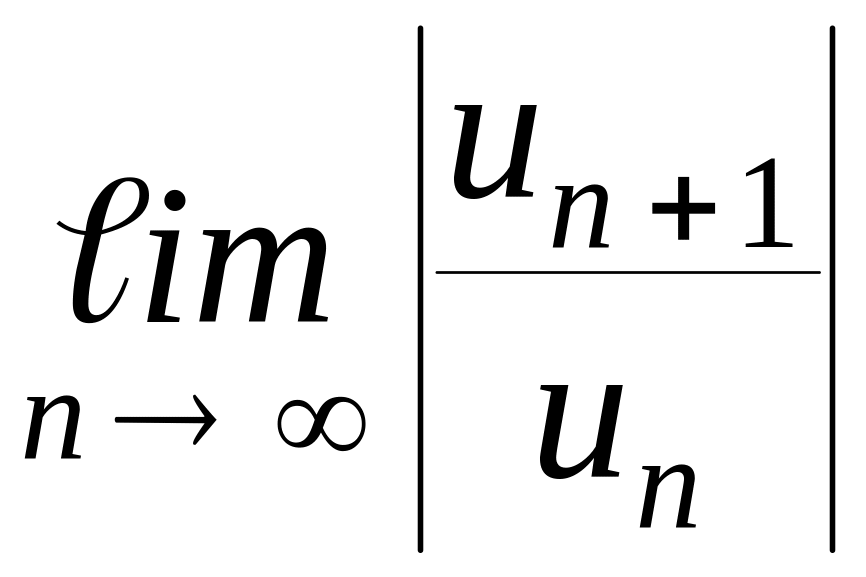

 или
(-1;1)
или
(-1;1)