§ 2. Необходимый признак сходимости ряда.

Следует отметить, что далеко не всегда сходимость или расходимость ряда удается установить, исходя из определения сходимости ряда, т.е. непосредственно из рассмотрения предела частичных сумм ряда. В большинстве случаев это весьма сложно. Поэтому для установления сходимости (или расходимости) ряда прибегают к использованию теорем, которые называются «признаками сходимости»

Теорема (необходимый признак сходимости).

Если ряд

сходится, то его общий член стремится к нулю при , то есть

Пример 1. Проверить, выполняется ли необходимый признак сходимости для ряда

Решение. Общий член Так как то необходимое условие сходимости (2) не выполняется. Следовательно, данный ряд расходится.

Пример 2. Проверить, выполняется ли необходимое условие сходимости (2) для ряда

Решение.

Как видно, необходимое условие сходимости (2) выполняется. Отметим, что из выполнения условия отнюдь не следует сходимость ряда.

Ряд (3) называется гармоническим. Этот ряд расходится, хотя для него выполняется необходимое условие сходимости (2).

§ 3. Основные свойства сходящихся рядов.

Свойство №1. Если ряд сходится и имеет сумму S, то его можно почленно умножить на одно и то же число

При этом полученный ряд

тоже сходится и имеет сумму CS.

Свойство №2 Сходящиеся ряды можно почленно складывать и вычитать. Если ряд сходится и имеет сумму А, а ряд сходится и имеет сумму В, то ряд сходится и имеет сумму А+В, а ряд сходится и имеет сумму А-В.

Свойство №3 Если ряд сходится, то сходится ряд, полученный из данного путем приписывания или отбрасывания любого конечного числа членов.

§ 4. Достаточные признаки сходимости,

основанные на сравнении рядов.

Признак сравнения 1

Если каждый член данного ряда с положительными членами

(А)

начиная с некоторого члена, не превосходит соответствующего члена другого заведомо сходящегося ряда

(В)

то данный ряд (А) тоже сходится.

Если же каждый член ряда (А), начиная с некоторого члена, не меньше соответствующего члена заведомо расходящегося ряда (В), то

данный ряд (А) тоже расходится.

Пример. Исследовать на сходимость ряд.

Решение. Сравним данный ряд с геометрической прогрессией

Ряд (*) сходится, так как знаменатель прогрессии

Члены данного ряда не превосходят соответствующих членов геометрической прогрессии (*). Следовательно, по признаку сравнения данный ряд также сходится.

Признак сравнения 2

Если при существует конечный отличный от нуля предел отношения общих членов рядов (А) и (В), то есть , то рассматриваемые ряды либо оба сходятся, либо оба расходятся.

Пример. Исследовать сходимость ряда

Решение. Общий член данного ряда Общий член расходящегося гармонического ряда Применяем признак сравнения 2. Так как

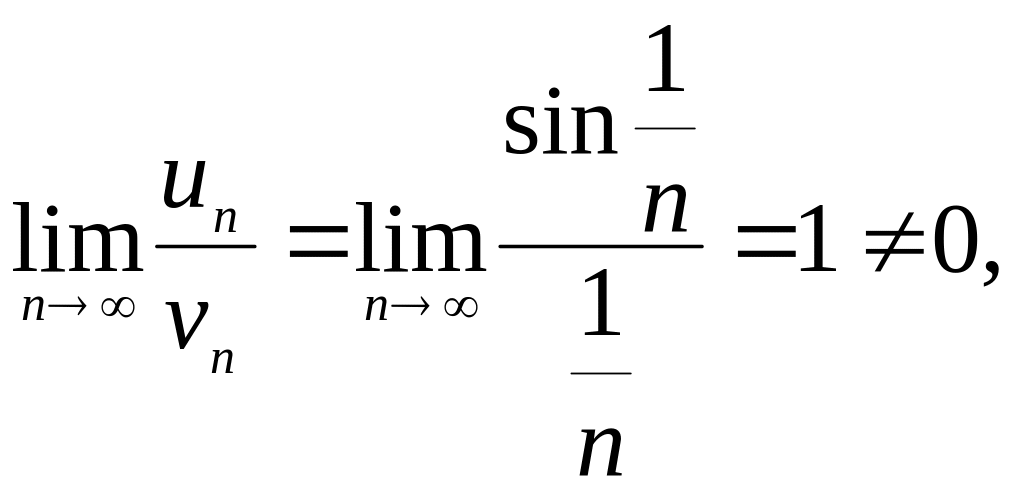
То исследуемый ряд расходится.