7Й вопрос. Момент инерции. Теорема Штейнера. Момент инерции однородных тел простейшей формы(стержень,цилиндр,шар).Расчет момента инерции однородного диска.

Момент инерции системы тела относительно данной оси называется физическая величина, равная сумме произведений масс N материальных точек системы на квадраты их расстояний до рассматриваемой оси.

J=(знак сум.:i=1;n)(mi•ri^2)

Теорема Штейнера-момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно парралельной оси, проходящей через центр масс C тела ,сложенному с произведением массы m тела на квадрат расстояния а между осями:

J=Jc+ma^2

Полый тонкостенный цилиндр радиусом R(ось симметрии) J=mR^2

Сплошной цилиндр или диск радиусом R(ось симметрии) J=mR^2/2

Прямой тонкий стержень длиной l(ось перпенд-на стержню и проходит через его середину) J=ml^2/12

Прямой тонкий стержень длиной l(ось перпенд-на стержню и проходит через его конец) J=ml^2/3

Шар радиусом R(ось проходит через центр) J=2mR^2/5

(см рис2).p(ро)-плотность матер.;r,dr.

dV=2Пи•r•dвки

dm=pdv

J=(простой интег)(dm•r^2)=(интег от 0 до R)(p•2Пи•r•dr•b•r^2)=2Пи•b•p(интегр от 0 до R)(r^3dr)=2Пи•b•p•R^4/4=(m=ПиR^2bp)=mR^2/2

8Й вопрос. Основной закон динамики вращ. Дв. ,его выводы на примере одной частицы. Внешние и внутренние силы.

Основной закон динамики вращательного движения твердого тела формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.

Производная момента импульса по времени, относительно полюса О равна моменту внешних сил относительно полюса.

dL/dt=M

(ситема из 3х ур-ий):

dLx/dt=Mx

dLy/dt=My

dLz/dt=Mz

Пусть вращение тела происходит вокруг оси z, т.е. вектор w сонаправлен с осью z,тогда

Lz=Jz•w

dLz/dt=d(Jz•w)/dt=Jz•dw/dt=Jz•E=Mz,где Е--эпсилон.

Mz=Jz•E

Вывод:

Везде вектора!!! L=[rp]=[r,mv]

dL/dt=d([r,mv])/dt=[dr/dt,mv]+[r,mdv/dt]=m[v,v]+[r,ma]=(т.к. m[v,v]=0 и ma=F)=[r,F]

9 й вопрос. Закон сохранения момента импульса для замкнутой системы. Сохраняющиеся величины-интегралы движения: законы сохранения энергии, импульса ,момента импульса .Кинетическая энергия частицы ,ее связь с работой результирующей силы.

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.         Это один из фундаментальных законов природы.         Аналогично для замкнутой системы тел, вращающихся вокруг оси z:

         отсюда                   или          .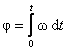

Импульс замкнутой системы сохраняется.

В системе тел между которыми действуют только консервативные силы- полная энергия сохраняется.

Кинетическая энергия механической системы -энергия механического движения этой системы.

Зависит от выбора системы отсчета.

Момент импульса замкнутой системы сохраняется, и не изменяется с течением времени.

В замкнутой системе момент внешних сил M=0 и dl/dt=0 откуда L=const

Гироскоп-массивное однородное тело, вращающиеся с большой угловой скоростью около оси своей симметрии, являющейся свободной осью.

Гироскоп сохраняет свое положение в пространстве тк моменты сил тяжести и трения относительно центра масс равны 0. Следовательно момент импульса гироскопа сохраняет свою величину и направления.

Чтобы ось гидроскопа изменила свое направление в пространстве,необходимо отличие от нуля момента внешних сил.Если момент внешних сил, приложенных к вращающемуся гидроскопу, относительно его центра масс отличен от нуля, то наблюдается явление,которое назыв. гидроскопическим эффектом.Оно состоит в том, что под действием пары сил F,приложенных к оси вращающегося гидроскопа,ось гидроскопа поворачивается вокруг прямой О3О3,а не вокруг прямой О2О2.