
- •Введение
- •1. Внешние и внутренние силы. Деформируемое тело.
- •2. Реальный объект и расчетная схема.
- •3. Основные допущения и гипотезы, принятые в
- •4. Метод сечений.
- •5. Понятие о напряжении. Предельное и допускаемое
- •6. Понятие о деформированном состоянии материала.
- •Геометрические характеристики плоских сечений
- •1. Статические моменты площади. Центр тяжести.
- •2. Моменты инерции плоских фигур.
- •3. Моменты инерции сложных сечений.
- •4. Моменты инерции относительно параллельных осей.
- •5. Зависимости моментов инерции при повороте
- •6. Определение направления главных осей.
- •Построение эпюр внутренних силовых факторов
- •1. Построение эпюр продольных сил при растяжении (сжатии).
- •1 Уч-к: ;
- •2 Уч-к: ;
- •2. Построение эпюр крутящих моментов.
- •3. Понятие о плоском поперечном изгибе. Балки и их опоры.
- •4. Построение эпюр при плоском изгибе.
- •5. Дифференциальные зависимости при изгибе.
- •Растяжение и сжатие
- •1. Напряжения в поперечных сечениях
- •2. Напряжения на наклонных площадках
- •3. Деформации при растяжении и сжатии. Закон Гука.
- •4. Условие прочности при растяжении. Типы задач.
- •5. Статически неопределимые конструкции.
- •6. Монтажные и температурные напряжения.
- •Опытное изучение механических свойств материалов
- •1. Опытное изучение свойств материалов при одноосном
- •2. Диаграмма растяжения стали марки сталь 3.
- •3. Разгрузка и повторное нагружение. Наклеп.
- •4. Диаграммы растяжения других конструкционных материалов
- •5. Испытание конструкционных материалов на сжатие.
- •Кручение
- •1. Чистый сдвиг. Закон Гука при чистом сдвиге.
- •2. Напряжения и деформации при кручении бруса
- •3. Расчет валов на прочность и жесткость при кручении.
- •4. Кручение стержней прямоугольного сечения.
- •Плоский изгиб
- •1. Нормальные напряжения при плоском изгибе.
- •2. Напряженное состояние прямого бруса
- •3. Расчет балок на прочность
- •4. Рациональные формы поперечных сечений балки
- •Перемещения при изгибе.
- •2. Дифференциальное уравнение упругой линии.
- •5. Понятие о начальных параметрах.
- •7. Примеры определения прогибов, расчет на жесткость.
- •8. Проверка балок на жесткость.
- •Теория напряженного и деформированного состояния в точке
- •1. Напряженное состояние в точке. Тензор напряжений.
- •2. Определение напряжений на наклонных площадках
- •3. Главные напряжения. Главные площадки.
- •4. Инварианты тензора напряжений.
- •5.Октаэдрические напряжения.
- •6. Понятие о шаровом тензоре напряжений и
- •7. Относительная объемная деформация.
- •8. Обобщенный закон Гука.
- •9. Потенциальная энергия деформаций.
- •Потенциальная энергия деформации и общие
- •1. Свойства упругих тел
- •2. Работа внешних сил.
- •3. Потенциальная энергия деформации упругой системы.
- •4. Интеграл Мора для вычисления перемещений
- •Приравниваем
- •5. Частные случаи записи интеграла Мора
- •6. Порядок определения перемещений по интегралу Мора
- •7. Правило Верещагина для вычисления интеграла Мора ("перемножение" эпюр)
- •8. Практические приемы перемножения
- •9. Теорема о взаимности работ и перемещений
- •Статически неопределимые системы
- •1. Понятие о статически неопределимых системах
- •2. Метод сил. Основная и эквивалентные системы
- •3. Канонические уравнения метода сил
- •4. Порядок расчета рамы по методу сил
- •5. Использование симметрии при расчете рам
- •6. Статически неопределимые балки.
- •7. Уравнение трех моментов.
- •Вычислим коэффициенты
- •8. Построение эпюры и определение опорных реакций для статически неопределимой балки.
- •Гипотезы прочности
- •В частном случае плоского напряженного состояния при , , условие прочности записывается в виде
- •Сложное сопртивление
- •2. Изгиб с растяжением (сжатием)
- •3. Косой изгиб. Пространственный изгиб.
- •4. Внецентренное сжатие (растяжение)
- •5. Изгиб с кручением круглых брусьев.
- •6. Изгиб с кручением прямоугольных брусьев.
4. Интеграл Мора для вычисления перемещений
произвольно нагруженных брусьев
Вывод
формулы проводится для случая плоского
изгиба, соответственно учитывается
только изгибающий момент
![]() .
В общем случае нагружения рассуждения
аналогичны.
.
В общем случае нагружения рассуждения
аналогичны.
Постановка задачи:
Задана
произвольная упругая система, загруженная
силами
![]() .
Требуется определить перемещение
произвольной точки
.
Требуется определить перемещение
произвольной точки![]() в заданном
направле-
в заданном
направле-
нии
![]() .
.
Для
вывода формулы кроме заданной рассмотрим
вспомогательную единичную систему,
которая представляет собой заданную
упругую систему (рис. 105), к которой
по направлению искомого перемещения
приложена единичная сила
![]() .
.
В ведем
обозначения:
ведем
обозначения:
в заданной системе -
изгибающий
момент -
![]()
работа
внешних сил -
![]()
энергия деформации -
-
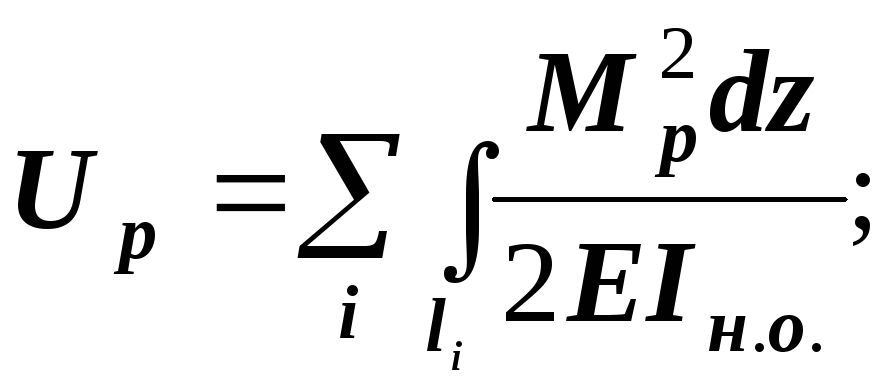
в единичной системе -
изгибающий
момент -
![]()
работа
силы -
![]()
энергия деформации -
-
![]()
По первому свойству упругих систем справедливы равенства:
![]()
![]()
Вывод формулы:
Загрузим
систему последовательно сначала
единичной силой
![]() ,
а затем, не
снимая ее, заданными силами
,
а затем, не
снимая ее, заданными силами
![]() .
Из равенства энергии и работы после
двух нагружений можно найти перемещение
.
Из равенства энергии и работы после
двух нагружений можно найти перемещение![]() .
.
Работа
после первого нагружения ![]() ,
,
после
второго нагружения
![]() ,
,
суммарная
![]() ,
,
Изгибающий
момент после двух нагружений
![]()
Вычисляем
![]()

![]()

Приравниваем
![]()
![]()
![]() ;
;
![]()
По аналогии можно вывести формулу интеграла Мора для всех случаев нагружения.
5. Частные случаи записи интеграла Мора
При расчете разных упругих систем учитывают соответствующие силовые факторы, поэтому используют разные формы записи интегралов Мора.
1. Для шарнирных стержневых систем:
![]()
2. Для плоских балок, рам и кривых брусьев
![]()
3. Для пространственных систем
![]()
6. Порядок определения перемещений по интегралу Мора
Д ля
определения перемещений надо рассмотреть
заданную и единичную системы. При
определении линейного перемещения по
направлению искомого перемещения
прикладывается единичная сила, а при
определении угла поворота сечения –
единичный момент.
ля
определения перемещений надо рассмотреть
заданную и единичную системы. При
определении линейного перемещения по
направлению искомого перемещения
прикладывается единичная сила, а при
определении угла поворота сечения –
единичный момент.
В
Рис. 106.![]() и
составляем интегралы Мора, вычислив
которые, получим величину искомого
перемещения.
и
составляем интегралы Мора, вычислив
которые, получим величину искомого
перемещения.
Участок
![]() :
:![]() Участок
Участок![]() :
:![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
7. Правило Верещагина для вычисления интеграла Мора ("перемножение" эпюр)
Интеграл Мора содержит силовые факторы от заданной нагрузки и единичных сил. Метод Верещагина основан на том, что эпюра от единичной силы и момента всегда прямолинейна, никогда не бывает параболы. Жесткость по участкам должна быть постоянной, чтобы ее можно было вынести за знак интеграла.
 Вывод
проводим на примере эпюр изгибающих
моментов (рис. 107), но результат справедлив
для любых эпюр, из которых одна линейная.
Вывод
проводим на примере эпюр изгибающих
моментов (рис. 107), но результат справедлив
для любых эпюр, из которых одна линейная.
Постановка
задачи: на участке балки
![]() с постоянной жесткостью
с постоянной жесткостью![]() заданы эпюры
заданы эпюры![]() и
и![]() .
Эпюра
.
Эпюра![]() имеет
произвольное очертание, эпюра
имеет
произвольное очертание, эпюра![]() - прямая линия без изломов.
- прямая линия без изломов.
Требуется вычислить интеграл
![]()
Вычисления:
![]()
![]()
![]()
![]()
![]()
![]()
Получено выражение, позволяющее вычислять интеграл Мора геометрически. Этот способ вычисления называется методом Верещагина.
Правило:
Чтобы
вычислить интеграл Мора по способу
Верещагина нужно построить эпюры
подинтегральных функций
![]() и
и![]() ,
а затем площадь эпюры
,
а затем площадь эпюры![]() ,
обозначаемую
,
обозначаемую![]() ,
умножить на ординату с эпюры
,
умножить на ординату с эпюры![]() расположенную под центром тяжести
площади
расположенную под центром тяжести
площади![]() ,
обозначенную -
,
обозначенную -![]() .
.
Примечание:
Если обе
"перемножаемые" эпюры прямолинейные,
то, можно, наоборот, площадь брать с
эпюры
![]() ,
а ординату с эпюры
,
а ординату с эпюры![]() .
.
![]() .
.
