Прочность

Прочность – способность детали сопротивляться разрушению или возникновению пластических деформации под действием нагрузки.

Прочность является основным критерием работоспособности большинства деталей машин.

Основным методом оценки прочности деталей машин является сравнение расчетных и допускаемых напряжений:

,

где σ, τ – расчетные нормальные и касательные напряжения, [σ] и [τ] – допустимые нормальные и касательные напряжения.

Также используется метод сравнения расчетных и допустимых коэффициентов запаса прочности:

S ≥ [S].

По характеру нагрузки прочность подразделяется на статическую, усталостную и ударную. По виду деформации – на объемную и поверхностную.

Основы расчета на объемную прочность подробно рассматриваются в курсе сопротивления материалов.

Рисунок 1.1 – Виды напряженного состояния

В зависимости от характера нагрузки различают следующие виды объемного напряженного состояния деталей машин:

а) напряжения растяжения (рисунок 1.1, а)

,

(1.1)

где F – внешняя нагрузка; А – площадь поперечного сечения детали; [σ_р] – допустимое напряжение растяжения.

Так как большинство деталей машин изготавливаются из стали, то напряжения сжатия также определяют по выражению (1.1).

б) напряжение изгиба (рисунок 1.1, б)

,

(1.2)

где M_max – максимальный изгибающий момент; W_x – осевой момент сопротивления; [σ_и] – допустимое напряжение изгиба.

Максимальный изгибающий момент определяют по эпюре изгибающих моментов, а осевой момент сопротивления для деталей круглого сечения по выражению

.

(1.3)

Тогда из условия прочности (1.2) следует

.

(1.4)

в) напряжения кручения (рисунок 1.1, в)

,

(1.5)

где Т – крутящий момент; W_р – полярный момент сопротивления; [τ_кр] – допустимое напряжение кручения.

Полярный момент сопротивления для деталей круглого сечения определяют по выражению

.

(1.6)

Тогда из условия прочности (1.5) следует

.

(1.7)

г) напряжения среза (рисунок 1.1, г)

,

(1.8)

где F – сдвигающее усилие; А_ср – площадь среза штифта; d – диаметр штифта; z – число штифтов; i – число стыков соединяемых деталей.

д) напряжения смятия (рисунок 1.1, г)

,

(1.9)

где F – сдвигающее усилие; А_см – площадь смятия; δ – толщина соединяемых деталей.

При сложном напряженном состоянии условие прочности имеет вид:

.

(1.10)

Объемная прочность является основным критерием работоспособности многих деталей. Непрочные детали не могут быть работоспособными. Допускаемые напряжения [σ] и [τ] представляют собой долю предельных (опасных) напряжений и определяются для типовых деталей экспериментальным путем или расчетом:

,

(1.11)

где σ_lim – одна из предельных прочностных характеристик материала детали; [s] = 1,5 ÷ 3 – допускаемый коэффициент запаса прочности.

Для стальных материалов в качестве предельной прочностной характеристики принимается предел текучести σ_т, а чугуна – временный предел прочности σ_в.

Поверхностная прочность представляет особый класс задач, связанных с первоначальным контактом деталей в точке или по линии (подшипники качения, зубчатые, фрикционные передачи и т. д.). В этом случае условие прочности имеет вид

,

(1.12)

где σ_Н и [σ_Н] – соответственно расчетные и допускаемые контактные напряжения.

Расчетные контактные напряжения σ_н сравнивают с допускаемыми контактными напряжениями [σ_Н], полученными экспериментально на реальных образцах. В расчетной практике наиболее широко используются схемы расчетов деталей с цилиндрическими поверхностями (рисунок 1.2).

Контактные напряжения возникают в месте соприкосновения двух тел в тех случаях, когда размеры площадки контакта несравненно малы (b / l → 0) по сравнению с размерами деталей 1 и 2.

Аналитическое решение контактной задачи было впервые получено известным немецким ученым Г. Герцем (1881 г.), о чем свидетельствует индекс «н» в обозначении контактных напряжений.

Рисунок 1.2 – Контакт двух цилиндров

В общем виде уравнение Герца имеет вид:

,

(1.13)

где Е_пр – приведенный модуль упругости; q – нагрузка на единицу длины контактной линии; ρ_пр – приведенный радиус кривизны контактирующих поверхностей; μ – коэффициент Пуассона (для стали μ ≈ 0,3).

Применительно к контакту двух цилиндров приведенный модуль упругости находят по выражению

,

(1.14)

где для стальных деталей Е₁ = Е₂ = Е = 2,1· 10⁵ МПа.

Приведенный радиус кривизны контактирующих поверхностей.

,

(1.15)

где знак плюс используется при внешнем зацеплении, а минус – внутреннем.

Нагрузка на единицу длины контактной линии

.

(1.16)

Для точечного контакта (шарикоподшипники) при площади контакта в виде эллипса (шар и плоскость) контактные напряжения

,

(1.17)

где а и b – длины полуосей эллиптической площадки контакта.
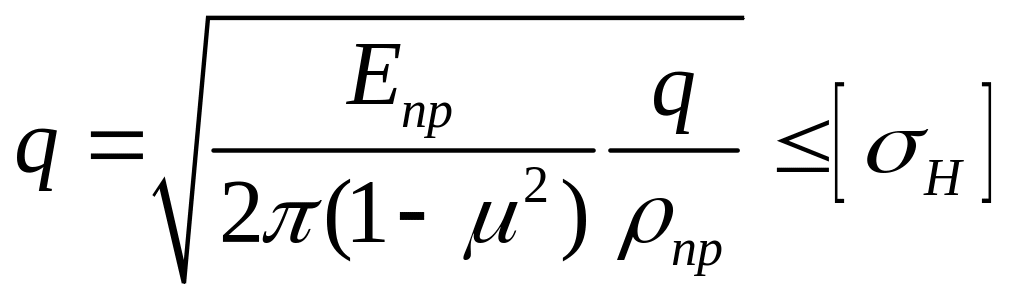