Міністерство освіти і науки України

Національний технічний університет України

«Київський політехнічний інститут»

Кафедра інформаційно-вимірювальної техніки

«ТЕОРІЯ ЕЛЕКТРИЧНИХ СИГНАЛІВ ТА КІЛ»

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторних занять

з кредитного модуля НП 06/2 «Теорія електричних сигналів та кіл -2».

Вимірювальні кола.

для студентів напряму підготовки

6.051001 «Метрологія та інформаційно-вимірювальні технології»

Рекомендовано кафедрою

інформаційно-вимірювальної техніки

Протокол № 24 від 1 квітня 2015 р.

Завідувач кафедри

____________________ Н.А. Яремчук

Київ – 2015

Методичні вказівки до лабораторних занять з дисципліни «Теорія електричних сигналів так кіл» для студентів напряму підготовки 6.051001 «Метрологія та інформаційно-вимірювальні технології» / Уклад.: К.Л. Серпілін, М.М.Мотін– К.: НТУУ «КПІ», 2015. – 72 с.

Затверджено на засіданні кафедри

інформаційно-вимірювальної техніки

(Протокол № _24_ від _1_квітня_ 2015 р.)

«Теорія електричних сигналів та кіл»

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторних занять

кредитного модуля НП 06/2 «Теорія електричних сигналів та кіл -2».

Вимірювальні кола.

для студентів спеціальностей

6.051001 «Метрологія та інформаційно-вимірювальні технології»

Укладачі:

Серпілін Клавдій Леонідович, к.т.н., доцент Мотін Максим Миколойович, асистент

Зміст

ТЕОРИЯ ЦЕПЕЙ. ВВОДНАЯ ЧАСТЬ..……………………………...……………… 4

Лаб. раб. №1. Определение характеристик измерительной аппаратуры…………. 4

Лаб. раб. №2. Характеристики цепей……………...…………………..……...……. 11

Лаб. раб. №3. Цепь верхних частот....……………………………………………… 15

Лаб. раб. №4. Цепь второго порядка….…………………………………………… 25

Лаб. раб. №5. Цепь нижних частот.…………………………………………………. 31

Лаб. раб. №6. Частотные и переходные характеристики пассивных цепей……... 38

Лаб. раб. №7. Спектральные характеристики процессов………………………….. 52

Лаб. раб. №8. Амплитудная модуляция гармонического носителя………………. 56

Лаб. раб. №9. Амплитудно-импульсная модуляция………………………………. 59

Лаб. раб. №10. Импульсная модуляция……………………………………………. 62

Лаб. раю. №11. Полосовые фильтры………………………………………………. 66

Лаю. раб. №12. Манипуляция сигналов…….…………………………………....... 69

Теория цепей. Вводная часть

Пассивная цепь представляет собой соединение пассивных элементов — резисторов, конденсаторов, катушек индуктивности — выполненное в соответствии с принципиальной электрической схемой. Схема является упрощенным представлением цепи. На схеме элементы представлены своими основными свойствами — сопротивлением, емкостью, индуктивностью, хотя каждый элемент наделен, до некоторой степени, всеми тремя свойствами, сопротивление, индуктивность и емкость соединительных проводников не учитывается, а схемные параметры подключаемых источников и измерительных приборов предполагаются идеальными. Поэтому расчет характеристик цепи по принципиальной схеме получается, до некоторой степени, приблизительным, и для его уточнения используют эквивалентные схемы, где учитываются те или иные дополнительные параметры. Увеличение числа параметров цепи обычно увеличивает и порядок описывающей её системы дифференциальных уравнений, который называют порядком модели цепи. Увеличение порядка модели не всегда увеличивает точность расчета характеристик цепи. Так, если при расчете цепи, состоящей из конденсатора и резистора учесть только емкость конденсатора и сопротивление резистора, получится модель первого порядка, а если учесть и индуктивность проводов — второго. Но значение этой индуктивности определится только при монтаже схемы, а на стадии расчета остается неизвестным, так что эта модель может использоваться только для оценки возможной погрешности моделирования цепи с помощью модели первого порядка. Поэтому при расчете характеристик цепи обычно используют минимальный порядок модели.

В частотной области цепь характеризуется комплексным коэффициентом передачи, его модулем, определяющим амплитудно-частотную характеристику (АЧХ ) и аргументом, задающим фазо-частотную характеристику (ФЧХ), и коэффициентом частотных искажений, являющимся нормированным коэффициентом передачи. Частотные характеристики определяются при гармоническом входном сигнале, когда напряжение или ток на входе цепи

, (1)

где Ax ,φx — амплитуда и фаза входного сигнала соответственно.

Тогда для линейной стационарной цепи выходной сигнал

, (2)

где — амплитуда и фаза выходного сигнала.

АЧХ цепи определяется зависимостью от частоты сигнала коэффициента передачи

, (3)

а ФЧХ — зависимостью от частоты сдвига фазы в цепи

. (4)

Область определения функции разделяют на полосу пропускания, полосу затухания и переходную полосу. По расположению этих полос можно разделить цепи на цепи нижних частот, цепи верхних частот и полосовые. Для цепей нижних частот полоса пропускания включает низкие частоты, и в том числе , для цепей верхних частот в начале координат расположена полоса затухания, а полоса пропускания включает неограниченное значение частоты. Для полосовой цепи полосы затухания находятся как в области низких, так и в области высоких частот. Значение коэффициента передачи для некоторой частоты из полосы пропускания принимается за номинальное значение , и тогда коэффициент частотных искажений

. (5)

При этом для цепи нижних частот номинальная частота должна быть как можно меньше , для цепи верхних частот — максимальной, а для полосовой цепи выбирается некоторое значение в центре полосы пропускания

Для цепи нижних частот первого порядка

., (6)

где частота соответствует значению коэффициента частотных искажений

и называется частотой среза цепи нижних частот. Для цепи верхних частот первого порядка

, (7)

где — частота среза цепи верхних частот.

Модели второго порядка используются, в частности, для описания цепей нижних частот и простейшей полосовой цепи. Для цепи нижних частот второго порядка коэффициент частотных искажений

, (8)

где λ — степень затухания, — собственная частота цепи. Экстремум функции (8) возможен при частоте

, (9)

и при этой частоте

. (10)

Полосовые цепи разделяют на узкополосные и широкополосные в зависимости от соотношения полосы пропускания и центральной частоты. Для узкополосной цепи коэффициент частотных искажений обычно представляют в виде

, (11)

где — центральная частота цепи, — добротность цепи. При малой добротности, когда , часто используется представление полосовой цепи как соединения цепи нижних и цепи верхних частот, когда (11) приводится к виду

, (12)

где 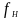— нижняя частота среза, — верхняя частота среза полосовой цепи, причем

. (13)

Для описания реакции линейной цепи на импульсный сигнал используется переходная характеристика, которая является нормированной реакцией цепи на ступенчатый сигнал. На практике вместо ступенчатого используется периодическая последовательность прямоугольных импульсов, причем длительность периода должна быть достаточной для практического окончания переходного процесса в цепи. Тогда переходная характеристика определяется функцией

, (14)

где — выходной сигнал цепи при ступенчатом (импульсном) входном сигнале,

— номинальная задержка сигнала в цепи, или интервал времени, по истечении которого выходной сигнал считается установившимся. Номинальная задержка зависит от вида цепи: для цепи нижних частот , для цепи верхних частот , для полосовой цепи . При моделях первого порядка переходная характеристика изменяется монотонно. Для цепи нижних частот первого порядка

, (15)

где постоянная времени цепи

. (16)

Для цепи верхних частот первого порядка

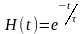(17)

где постоянная времени

. (18)

Переходная характеристика цепи нижних частот второго порядка при <1

, (19)

где , . Погрешность установления в этом случае знакопеременна, и поэтому такой переходной процесс часто называют колебательным. Интервал между нулевыми значениями погрешности установления определяется из уравнения

,

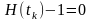так что для первого интервала из (15) получим

. (20)

Значение первого экстремума функции (15)

. (21)

Переходная характеристика цепи нижних частот второго порядка при >1

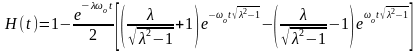. (22)

Переходная характеристика полосовой цепи при >0.5

, (23)

и равна нулю в точке

, (24)

а отношение амплитуд двух первых экстремальных значений

. (25)

Переходная характеристика полосовой цепи при <0.5 обычно строится с использованием (13), так что в этом случае

, где (26)

причем экстремум функции находится в точке

, (27)

а отношение значений функции и при и

(28)

Для цепи верхних частот можно считать << , и тогда из (12)

получаем

, (29)

а из (26) соответственно

(30)

Описание объекта

Принципиальные схемы исследуемых цепей приведены на рис. 1. Значения резисторов R1 определяются положением переключателя SW3 на макете, и выбираются из ряда 56, 180, 510, 910 Ω, а значения R2 — из ряда 180, 510, 910, 8200 Ω переключателем SW4. Реактивные элементы одинаковы для всех схем и составляют C = 6800 pF, L = 0.2 mH. Значения R1 и R2 устанавливаются в соответствии с номером бригады по табл 1.1

1.1 1.2 1.3 1.4

Рис. 1.Принципиальные схемы исследуемых цепей

Выбор схемы для исследований определяется переключателями SW1 и SW2 в соответствии с таблицей на крышке макета, причем SW1 определяет строку, а SW2