24

Лекция № 7. Математические модели динамических систем, представленных в пространстве состояний

Вопросы

7.1. Общая характеристика представлений моделей в пространстве состояний

7.2. Состояния управляемых систем.

7.3. Представление моделей детерминированных динамических систем.

7.3.1. Модели роста и насыщения макросостояний динамических систем.

7.3.2. Система в состоянии катастрофы.

7.4. Представление линейных динамических систем.

7.5. Методы переменных состояния. Случайные марковские модели.

7.6. Модели связности структур динамических систем.

Литература

1. Поповский В.В., Олейник В.Ф. Математические основы управления и адаптации в телекоммуникационных системах. Х. СМИТ, 2011. П.16 стр.335-338.

2. Методы научных исследований в телекоммуникациях. Х. СМИТ. §25,26,27,28. стр.64-79.

Дополнительная литература

1. Сейдж Э. Мэлс Дж. Теория оценивания и ее применение в связи и управлении. М. Связь, 1976 г.

Введение

В предыдущих лекциях основное внимание уделялось методам представления моделей, анализу и синтезу, основанным на использовании плотности или функции распределения вероятностей состояния рассматриваемых моделей.

Использование вероятностных характеристик для моделирования динамики чрезвычайно громоздко, а ограничение эргодичности, позволяющее упростить решение задачи исключает возможность моделирования динамики систем. Динамика, в том числе нелинейная или нестационарная адекватно моделируется дифференциальными или разностными уравнениями в пространстве состояний.

Очевидно, что моделирование в пространстве состояний является более общим, адекватным и полным представлением, поскольку отображают состояние всей системы, а не только ее части в виде вероятностных характеристик и может применяться как к процессам и помехам, так и событиям и величинам.

Здесь наше внимание будет уделено детерминистским и вероятностным моделям представимых самими состояниями.

7.1. Общая характеристика представлений моделей в пространстве состояний

Динамические (инерционные) системы характеризуются тем, что их состояние изменяется во времени и (или) пространстве после появления внешнего воздействия. Динамические системы (ДС) бывают детерминированы или случайны, одномерны и многомерны и др. Все эти свойства применимы для моделей ТК-систем, в зависимости от контекста решаемой задачи. Мы ограничимся рассмотрением случайных линейных моделей, что на практике чаще всего применяется.

Ранее были рассмотрены динамические системы, в том числе системы массового обслуживания представимые вероятностями состояний , что позволяет решать многие задачи. Альтернативным является метод представления самими состояниями , что позволяет в большей мере отображать сущность динамики поведения.

Инерционность динамических систем характеризуется производной от состояния и выражается дифференциальным уравнением (уравнением состояния):

,

где 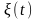- представляется моделью внешних воздействий, в числе которых могут быть как вредные (помехи), так и полезные (управление) воздействия;

или - коэффициент состояния, показатель инерционности системы, в частном случае величина, обратная интервалу корреляции состояния системы.

Такое представление дает основание называть динамическую систему дифференциальной. Разнообразие видов дифференциальных уравнений позволяет моделировать множество динамических систем с различными свойствами. Рассмотрим наиболее характерные свойства динамических систем в пространстве состояний.

7.2. Состояния управляемых систем

Состояния системы удобно иллюстрировать траекториями на плоскости (рис.7.1).

Рис.7.1. Траектория движения динамических систем с различным состоянием: 1. Равновесное. 2. Переходное. 3. Стационарное. 4. Критическое. 5. Катастрофическое

1. Равновесное состояние. Автономное состояние покоя в отсутствии внешних воздействий. Уравнение состояния системы в состоянии покоя

. (7.1)

2. Переходное состояние. Автономная система возвращается в равновесное состояние после снятия внешнего воздействия. Уравнение состояния такой системы

, . (7.2)

3. Стационарное состояние. Устойчивое состояние, когда внешние воздействия носят стационарный характер. Уравнение состояния такой системы

, (7.3)

где - внешнее воздействие.

Для неустойчивых систем стационарное состояние не наступает, система приобретает критический или катастрофический характер.

4. Критическое состояние. Пограничное состояние между устойчивым и неустойчивым. При дальнейших воздействиях траектории состояния приобретают множественный характер. Уравнение состояния может быть вида (7.3), при .

5. Катастрофическое состояние. В уравнении (7.3) . Хаотическое состояние. Состояние системы после точки бифуркации (Т.Б.) может приобретать любое значение в области ограниченной двумя пунктирными огибающими.

На практике состояние системы зависит не только от коэффициента А, но и от В, от величины шага дискретизации и других параметров. Эти зависимости будут проанализированы и представлены ниже.